[Linear Algebra] 2.4 Vector Space

이번 글에서는 벡터 공간(Vector Space)에 대해서 살펴보겠습니다.

1. 벡터 공간(Vector Space)

Vector Space란 9개의 공리를 만족하는 두 개의 operation(vector addition, scalar multiplation) 연산이 정의되는 집합을 말합니다.

9가지 공리

9가지 조건들에 대해서 다뤄보겠습니다.

• 벡터 덧셈
  - "덧셈에 대해 닫혀있다": $V_n$ 집합에 $v_1, v_2$가 있을 때, $v_1 + v_2$의 결과도 $v_n$에 있음을 말합니다.
  - 교환 법칙: $V_n$ 집합에 $v_1$,$v_2$가 있을 때, $v_1 + v_2 = v_2 + v_1$을 만족한다.
  - 결합 법칙: $V_n$ 집합에 $v_1,v_2,v_3$가 있을 때, $v_1+(v_2+v_3) = (v_1 + v_2) +v_3$을 만족한다.
  - 항등원: $V_n$ 집합에 $v_1$이 있고 $e$가 존재할 때, $v_1 + e=v_1$을 만족한다. 이때 $e$를 0이라고 쓴다.
  - 역원: $V_n$ 집합에 $v_1, x$가 있을 때, $v_1 + x = 0$을 만족한다. 이때 $x$를 $-v_1$이라고 쓴다.
• 스칼라 배
  - "스칼라 배에 대해 닫혀있다": $R$에 $k$가 있고, $V_n$에 $v_1$이 있을 때 $kv_1$이 $V_n$안에 있음을 말합니다.
  - 결합 법칙:
  - 항등원:
  - 분배 법칙:

2. 부분공간(Vector Subspace)

벡터공간 $V_n$의 부분집합 $W_n$이 벡터공간이면 $W_n$을 $V_n$의 부분공간이라고 말합니다.

• 벡터공간 $V$에 대해 자명한 부분공간은 $V$자신과 {0}입니다.
• 아래 그림들 중에 부분공간은 D하나 뿐입니다.
  
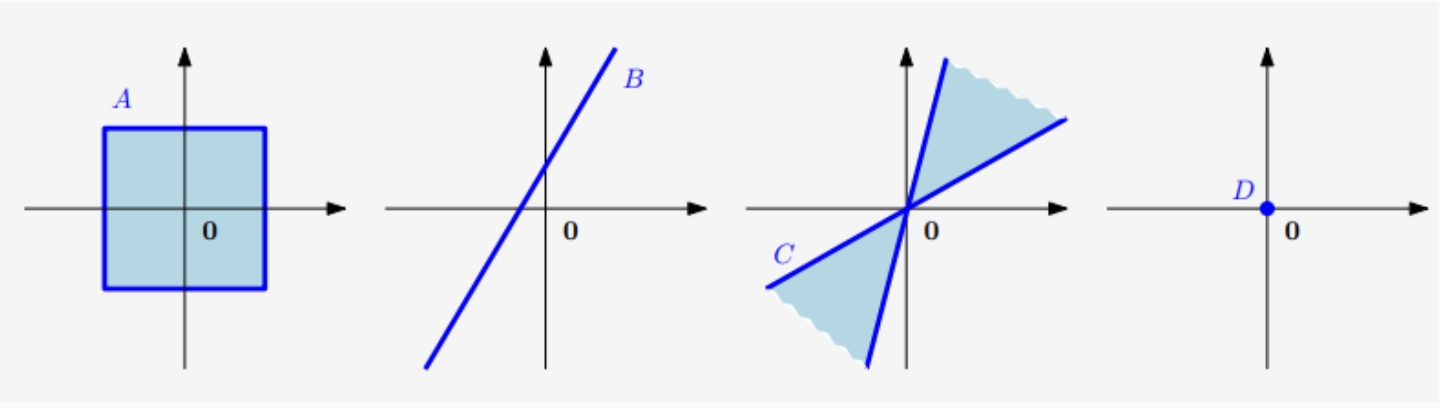
• A와 C는 multiplation에 대해 닫혀있지 않기 때문에 부분공간이 아닙니다.
• B는 0을 포함하지 않기 때문에 부분공간이 아닙니다.

다시 살펴보면서 부분공간의 성질에 대한 추가설명

다음 글에서는 선형 독립(Linear Idependence)에 대해서 포스팅하도록 하겠습니다.