[Linear Algebra] 2.2 Matrix
이번 글에서는 행렬이 무엇인지?
이 행렬을 가지고 어떠한 연산들을 수행할 수 있는지? 에 대해서 이야기 해보려고 합니다.
1. 행렬(Matrix)
- 위에 행렬을 보면 알 수 있듯이 행(Row)과 열(Column)에 맞추어 직사각형 모양으로 순서 있게 배 열하여 괄호[ ]로 묶은 것을 행렬이라고 합니다.
- M개의 행렬과 N개의 열로 구성된 행렬을 M X N 행렬이라고 합니다.
- 행렬의 차원(Dimention)은 행렬의 크기를 말합니다.
2. 행렬 덧셈과 곱셈(Matrix Addition and Multiplication)
- 행렬 덧셈 (Matrix Addition)
- M x N 크기의 행렬 A가 있을 때, 같은 크기인 행렬만 덧셈이 가능합니다.
- 아래 행렬 A와 B의 덧셈을 예시를 보여드리겠습니다.-행렬 A와 B을 더한 결과 행렬도 똑같이 M x N 크기의 행렬이 됩니다.
- 행렬 곱셈 (Matrix Multiplication)
- M x N 크기의 행렬 A가 있을 때, A의 열과 같은 크기의 행을 가진 N x K 크기의 행렬 B는 곱셈이 가능합니다.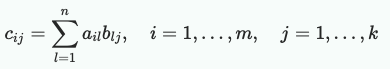
- 즉, A의 i번째 행의 요소와 B의 j번째 열의 요소들을 곱해서 더한 것과 같습니다.
- 이를 내적(dot product)이라고 합니다. - 행렬의 성질
- 행렬과 행렬의 곱은 순서를 지켜줘야하기 때문에 교환법칙이 성립하지 않습니다.
- 결합 법칙(Associativity)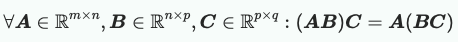
- 분배 법칙(Distributivity)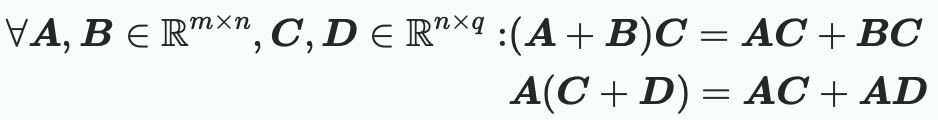
- 단위 행렬과의 연산(Mul with the identity matrix)- 단위 행렬:쉽게 말해 어떤 행렬 A가 있을 때, 행렬 곱셈 수행시 자기 자신이 결과로 나오게 하는 행렬을 말합니다.
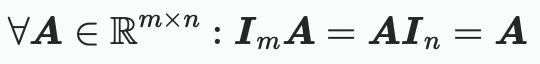
- 단위 행렬:쉽게 말해 어떤 행렬 A가 있을 때, 행렬 곱셈 수행시 자기 자신이 결과로 나오게 하는 행렬을 말합니다.
3. 역행렬과 전치행렬(Inverse and Transpose)
역행렬의 정의
A 행렬이 n x n인 정사각 행렬일 때
를 만족하는 n x n 행렬 B를 A의 역행렬이라고 하며 로 표기합니다.
- 한글로 풀어서 말하자면 행렬 A에 행렬 B를 곱했을 때 항등행렬이 결과로 나오게 만드는 행렬 B를 A의 역행렬이라고 합니다.
- 역행렬을 구하는 방법으로는 가우스-조던 소거법(Gauss-Jordan Elimaination)이 있는데 다음 포스팅에서 자세히 다루도록 하겠습니다.
전치행렬의 정의
m x n 크기인 행렬 A에 대하여 B의 크기가 n x m이고, 인 행렬 B를 A의 전치행렬이라고 합니다.
- 는 의 열을 행으로 바꿔서 찾을 수 있습니다.
대칭 행렬 (Symmetric Matrix)
를 만족하는 행렬 A는 Symmetric하다고 표현하고, 이를 Symmetric Matrix라고 합니다.
- 무조건 m x m 크기의 정사각 행렬만 Symmetric할 수 있습니다.
4. 스칼라 곱(Multiplication by a Scalar)
스칼라 λ를 mxn크기의 행렬에 곱할 수 있습니다.
라고 했을 때, B의 안의 값들은 가 됩니다.
다음은 역행렬을 구하기 위한 가우스-조던 소거법에 대해서 포스팅하겠습니다.
