이번 글에서는 기저와 랭크에 대해서 다뤄보도록 하겠습니다.
1. 기저(Basis)
기저란 어떤 벡터 공간이 있을 때 그 공간을 span하는 linearly independent한 벡터들을 말합니다. 여기서 span은 linear combination으로 나타낼 수 있는 벡터의 영역을 말합니다.
쉽게 말해서 어떤 공간을 이루는 필수적인 구성요소라고 할 수 있습니다.
예를들어 2차원 좌표평면 전체를 span할 수 있는 basis를 찾는다고 할 때 대표적인 basis는
입니다.
- 2차원 평면 전체를 나타낼 수 있고 linearly independent하기 때문에 기저라고 할 수 있습니다.
반대로
- 이는 span하면 나타낼 수는 있으나 linearly independent하지 않기 때문에 기저라고 할 수 없습니다.
2. 랭크(Rank)
랭크란 행렬이 가지는 independent한 column의 수를 말합니다.
즉, column space의 차원(dimension)을 말합니다. 여기서 column space란 column이 span하는 space를 말합니다.
또, 굉장히 중요한 성질은 Independent한 column의 수와 Independent한 row의 수는 무조건 같습니다.
왜냐하면 가 성립하기 때문입니다.
예시와 함께 rank의 성질을 보여드리겠습니다.
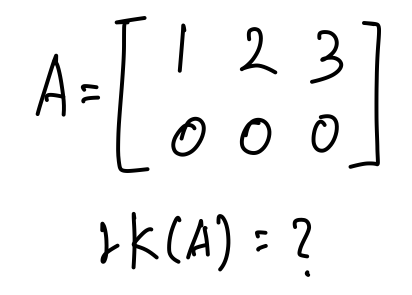
- 정답을 먼저 말씀드리자면 rk(A)는 1입니다.
- 왜냐하면 위 행렬에서 independent한 column의 수는 1개이기 때문입니다.
- 또 위 행렬은 2 x 3크기의 행렬이지만 rank는 1이기 때문에 rank-difficient라고 합니다.
- 만약 2 x 3 크기의 행렬이 rank가 2라면 이는 rank수 만큼 row가 꽉 차있기 때문에 full-row rank라고 할 수 있습니다.
- 또 3 x 2크기의 행렬이 rank가 2라면 이는 full-column rank라고 할 수 있습니다.
- 마지막으로 3 x 3크기의 행렬이 rank가 3이라면 full-rank라고 할 수 있습니다.
다음 글에서는 Linear Mappings에 대해서 포스팅하도록 하겠습니다.
정진.