Decoder-only Model Review

Decoder-only 모델의 대표적인 예시로 GPT가 있다. GPT은 다음 토큰을 예측하는 모델인데, 이것이 생성 task와 완전히 동일하기 때문에 이 강점들이 generative AI의 목적에 부합한다.
Decoder-only Model의 3가지 특징

• Auto Regressive Sequential prediction based on previously generated tokens. 자기가 생성을 한 것을 자기가 다시 학습한다.
• Self-Attention Captures relationships between words within the sequence. 문장에서 어떤 단어가 가장 큰 중요도를 가지는지 계산한다.
• Causal Masking Blocks future tokens, ensuring sequential generation order. 다음 토큰을 예측한다.

LLaMA

Meta AI에서 내놓은 오픈소스 모델. 2023년 2월에 LLaMA 1이 출시되었다. 언어 뿐만 아니라 이미지 처리까지도 가능하다.

Understanding LLaMA Model Flow

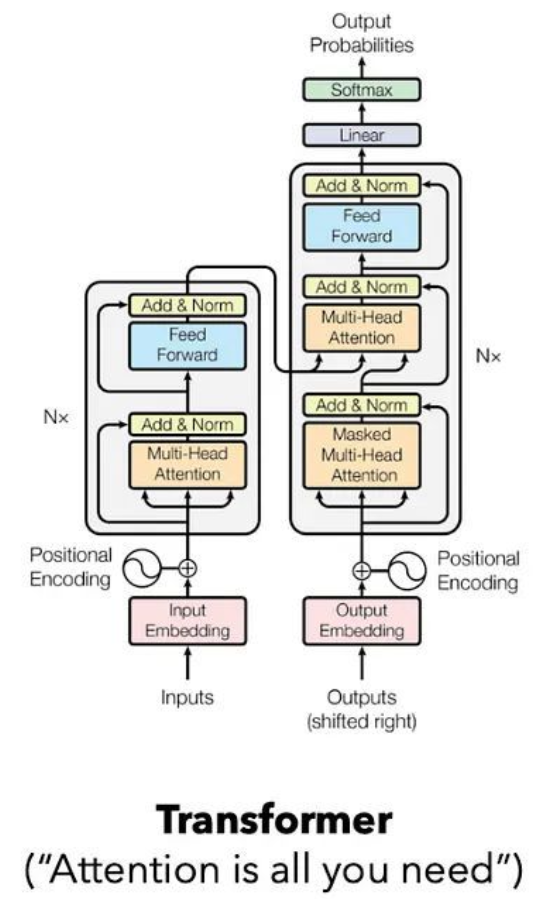
• Transformer의 Decoder 부분을 따서 LLaMA 모델을 만들었다.
• GPT2 같은 경우는 정말 디코더 부분을 똑 따와서 만들었는데, LLaMA3은 좀 더 개선되었다.
  
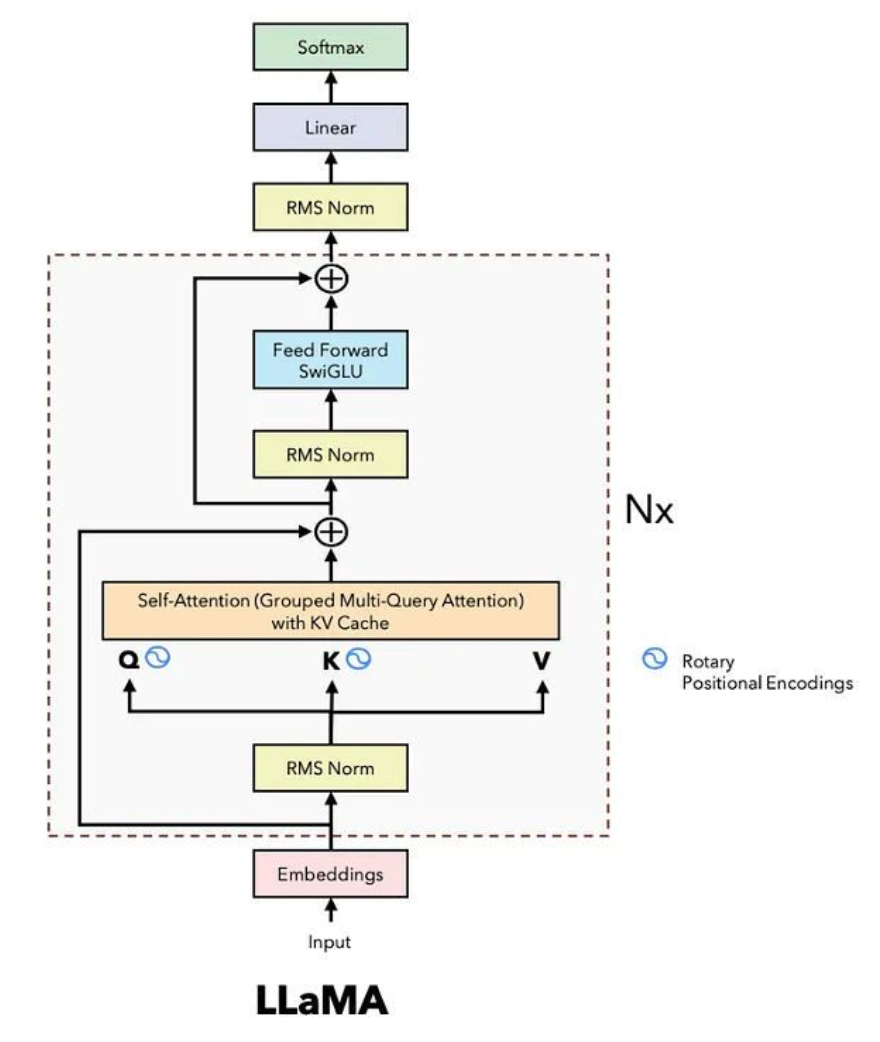
  Transformer의 디코더 부분은, attention을 계산할 때 각각의 토큰은 위치 정보를 가지고 있지 않다.

1. 따라서 LLaMA 구조에서는, Rotary Positional Encoding(RoPE)을 도입하여 위치 정보를 알려주었다. Attention 매커니즘 안에 query-key 부분에 위치 정보를 넣어준다. 따라서 attention layer이 한번 계산될 때마다, rotary embedding의 위치 정보를 함께 계산을 해줌으로써 상대적인 위치 정보와 절대적인 정보를 같이 이해하면서 attention에서 모든 layer에서 위치를 이해하면서 계산할 수 있게 되었다.
2. LLaMA은 RMSNorm이라는 더 간소화된 layer normalization 방식을 사용하여 더 빠르고 효율적으로 계산한다. 또한 RMSNormdms attention 이전에 적용되어 학습과 추론 속도를 높이고, 모델의 안정성과 성능 또한 극대화시켰다.
3. LLaMA은 feed-forward 단계에서 SwiGLU(스위글루)라는 활성화 함수를 사용하여 데이터를 더 효율적으로 처리했다. 스위글루는 Swish(스위시)라는 활성화 함수와 이전에 사용했던 GLU 방식을 결합하여 데이터를 더 효율적으로 처리하는 매커니즘이다.
4. Softmax와 Linear 부분에서는 NN.linear으로 불리는 레이어를 사용한다. 이 레이어는 hidden vector에서 출력된 값을 소프트맥스를 통해 다음에 나올 토큰을 예측하는 방식으로 동작한다.
5. 또한 LLaMA 모델부터는 GQA(Grouped Query Attention)이라는 기법도 함께 사용했다.

---

Code-level Analysis of LLaMA

Rotary Embedding의 구현 방식

Rotary embedding은 2023년 RoFormer 논문에서 처음 제안되었다. 로터리 임베딩의 핵심은 임베딩 계산 시 Rotary Trasnformer(회전 변환)을 사용해 위치 정보를 인코딩하는 것이었다.

이 행렬을 $x$좌표와 $y$좌표에 적용하면, 특정 각도 $\theta$만큼 회전된 새로운 좌표를 얻을 수 있다.

이를 쿼리, 키 벡터에 적용해보자. 예를 들어 16차원의 쿼리 벡터가 있다면, 이를 2차원 벡터 8개로 분할할 수 있다. 이 8개의 벡터는 $(x, y)$으로 표현할 수 있다.
각각의 2차원 벡터에 대해 회전 변환을 적용하면, 새로운 $(x', y')$값이 나온다. 여기서 각 벡터는 코사인과 사인 값을 기반으로 상대적인 위치 정보를 인코딩하게 된다.

위치 정보 인코딩 예시
첫번째 벡터의 경우, 각도 $\theta_1$으로 회전한 $(x_1', y_1')$이 생성된다. 만약 두번째 벡터가 있다면, 각도 $\theta_2$으로 회전한 $(x_2', y_2')$을 계산한다.
이렇게 모든 벡터가 상대적인 위치 정보를 포함한 형태로 변환되며, 원래의 16차원 벡터가 위치 정보가 포함된 형태로 복원된다.
상대적 위치 정보
이 방식의 중요한 특징은 두 벡터 간의 상대적 거리를 각도로 나타낼 수 있다는 점이다.
예를 들어, 벡터 1과 벡터 2의 차이는 $\theta_1 - \theta_2$만큼의 회전 각도 차이를 가진다.

이러한 상대적 각도 차이를 통해 모델은 토큰 간의 상대적 위치 관계를 학습하게 된다. 따라서 rotary embedding은 위치 정보를 제공하는 방식이 기존 방식보다 유연하며, 위치 변화에 더 강한 성능을 발휘한다.

절대적 위치 임베딩	로터리 임베딩
각 토큰의 고유한 위치 정보를 임베딩	토큰 간의 상대적 위치 정보를 인코딩
문장 길이에 따라 고정적	문장 길이에 따라 유연
모델이 긴 문장 처리 시 성능 저하 가능	긴 문장에서도 효율적 학습 가능
추가 파라미터 필요	수학적 변환으로 추가 파라미터 불필요

Code