| 문제에 앞서..
코딩테스트에서 "소수"를 구하는 문제는 일반적으로
"에라토스테네스의 체" 방법을 이용해 해결한다.
-
소수 구하기
=> 수학적인 코딩테스트 문제가 나왔을 때 빈번하게 출제되는 유형
=> 대표적인 판별법 : "에라토스테네스의 체" -
소수
: 1과 자기 자신 외에 약수가 존재하지 않는 수
에라토스테네스의 체
1) 구하고자 하는 소수의 범위만큼 1차원 배열을 생성
2) 2부터 시작하고 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지움.
//1은 소수가 아니므로 예외하고 2부터 탐색
이 때 처음으로 선택된 숫자는 지우지 않음
3) 배열의 끝까지 2)를 반복한 후 배열에서 남아있는 모든 수를 출력🪄탐색은 소수값을 구하려는 값의 제곱근까지만 탐색한다.
why?
예를들어 N의 소수들을 구할 때,
a*b는 모두 N의 제곱근보다 클 수 없다.
따라서 N의 제곱근까지만 확인해도 전체 범위의 소수를 판별할 수 있다.
ex) 16의 범위까지 소수를 구할 때,
16은 4*4로 이루어지면 16보다 작은 숫자는 항상 4보다 작은 약수를 갖게 된다는 뜻
'에라토스테네스의 체' 원리
ex) 1~30까지의 수 중 소수 구하기
1. 1~30까지 1차원 배열 생성
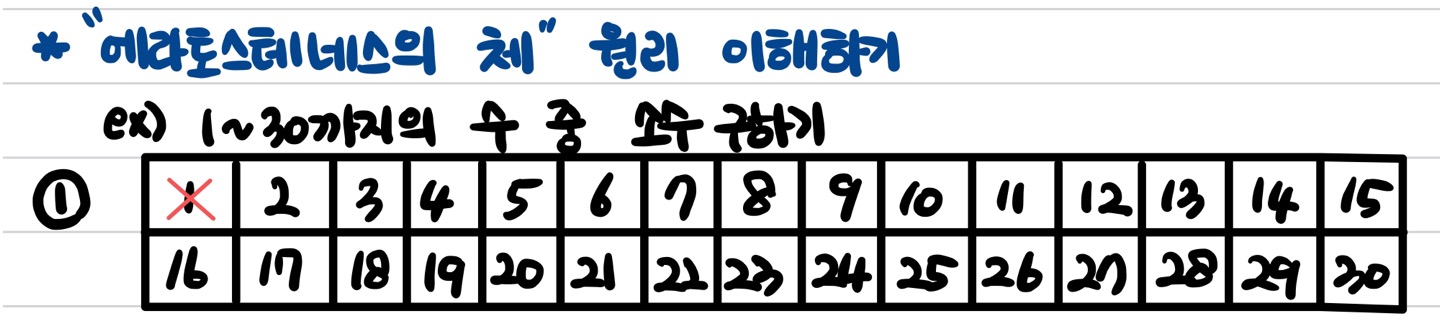
2. 1은 소수가 아니므로 2부터 시작하며 처음으로 선택된 2는 삭제하지 않고,
2의 배수들 모두 삭제

3. 다음 지워지지 않은 수 3, 3의 배수들 모두 삭제!
4. 앞의 작업들을 반복한다.
5. 삭제되지 않은 모든 수 출력
=>코드 작성할 때는 x 친 값의 자리에 0을 넣어 판별하고,
=> 출력시에 0이 아닌 값들만 출력하여 확인한다.
🤷♀️ '에라토스테네스의 체' 사용할 때 시간 복잡도는?
: 일반적으로 에라토스테네스의 체를 구현하려면 이중 for문을 이용하므로 시간 복잡도가 O(N^2) 정도라고 판단할 수 있다.
그러나, 실제 시간 복잡도는 최적화의 정도에 따라 다르겠지만, 일반적으로 O(Nlong(logN))이다.
그 이유는 배수를 삭제하는 연산으로 실제 구현에서 바깥쪽 for문을 생략하는 경우가 빈번하게 발생했기 때문이다.
이러한 이유 때문에 에라토스테네스의 체 기법은 현재에도 코딩테스트에서 소수를 구하는 일반적인 방법으로 통용되고 있다.
| 내가 푼 문제
백준 - 1929(링크 첨부 예정)
