동적 계획법(Dynamic Programming)
: 복잡한 문제를 여러개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법
: 코딩테스트에서 중요한 영역
동적 계획법의 핵심 이론
1) 큰 문제를 작은 문제로 나눌 수 있어야 한다.
2) 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들의 결괏값은 항상 같아야 한다.
3) 모든 작은 문제들은 한 번만 계산해 DP테이블에 저장하며, 추후 재사용할 때는 이 DP테이블을 이용한다.
이를 메모이제이션(memoization)이라고 한다.
4) 동적 계획법은 탑-다운(top-down)과 바텀-업(bottom-up) 방식으로 구현할 수 있다.
피보나치 수열
: 동적 계획법의 가장 대표적인 문제
: 피보나치 수열 공식 자체가 동적 계획법의 점화식이라고 생각하자!
// N번째 수열 = N-1번째 수열 + N-2번째 수열
- D[N] = D[N-1] + D[N-2]
ex) 1 1 2 3 5 // 5=3+2
1 1 2 3 5 ? // ? = 3+5 따라서 8
사용법
1) 동적 계획법으로 문제를 해결할 수 있는지 확인하기
ex)
6번째 ? 에 들어올 수열은 5번째 피보나치 수열과 4번째 피보나치 수열의 합
// 큰 문제 : 6번째 피보나치 수열
// 작은 문제로 쪼개기 : 5번째, 4번째 수열(각 수열의 값은 항상 같다.) -> 그러므로 DP로 풀 수 있겠다 판단한다.
1 1 2 3 5 ?
2) 점화식 세우기
: 논리적으로 전체 문제를 나누고, 전체 문제와 부분 문제간의 *인과 관계를 파악하는 훈련이 필요하다.
- 인과 관계를 파악하는 방법은 개인차가 있다.
내가 학습한 교재에서는 '10장 조합'이론에서 설명!
(포스팅 후 링크 첨부 예정)
ex)
6번째 수열을 구해야 할 때,
1~5번째 수열이 이미 구해져있다고 가정을하고,
1~5번째 수열로 어떻게 6번째 수열을 만들 수 있을지 고민을하며 인과 관계를 찾는다.
6번째 = 5번째 + 4번째
// 공식 & 점화식
일반화 => N번째 = N-1번째 + N-2번째
DP 테이블 => D[N] = D[N-1] + D[N-2]
3) 메모이제이션(memoization) 원리 이해하기
: 메모이제이션은 부분 문제를 풀었을 때 이 문제를 DP 테이블에 저장해놓고, 다음에 같은 문제가 나왔을 때 재계산하지 않고 DP테이블의 값을 이용하는 것
아래와 같이 재귀함수를 구현했을 때,
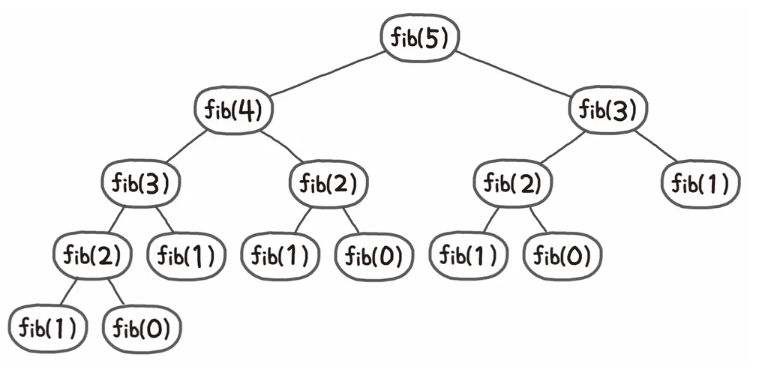
fib(2), fib(3)을 DP테이블에 저장해놓고, 같은 문제가 나왔을 때 재계산하지 않고 DP테이블의 값을 이용
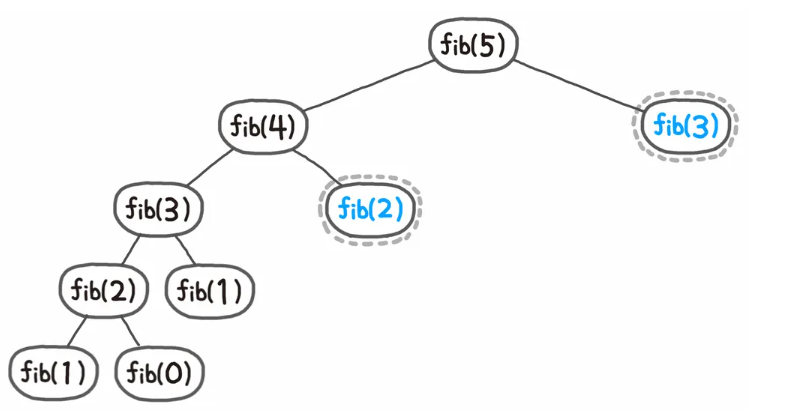
- 탑-다운(top-down) 구현 방식 이해하기
- 위에서부터 문제를 파악해 내려오는 방식
- 재귀 함수 형태로 코드를 구현
=> 가독성이 좋고 이해하기 쉽다.
- 바텀-업(bottom-up) 구현 방식 이해하기
- 가장 작은 부분 문제부터 문제를 해결하면서 점점 큰 문제로 확장하는 방식,
- 주로 반복문(while, for문) 형태로 구현
: 탑-다운 / 바텀- 업 방식 중 좀 더 안전한 방식은 바텀-업 방식이다.
탑- 다운 방식은 재귀 함수의 형태로 구현되어 있기 때문에 재귀의 깊이가 매우 깊어질 경우 런타임 에러가 발생할 수 있다.
- 탑-다운 방식으로 구현했는데 런타임 에러가 발생한 경우?
1) 바텀-업 방식으로만 구현해야 하는 것은 아닌지 확인
2) 탑-다운으로 구현한 점화식 (함수)가 최적화 되어있는가 확인
| 출처
Do it 알고리즘 with 자바편
나무위키(메모이제이션 사진)
| 내가 푼 문제
백준- 9095 , 9655 (포스팅 및 추가 문제 업로드 예정)
