
1. Probablity Theory
Sample space ( 또는 Ω ) :
ex : 주사위 -> 1~6까지의 수 ,
실수인 경우 조건제시, 정수인 경우 원소 나열법으로 표현되는 것이 일반적.
Ω의 부분집합 : Event (공집합, Ω의 전체집합 포함)
ex : 주사위에서 짝수만 나왔다. A = {2, 4, 6} ⊂ Ω
2. Boolean Algebra (Algebra of events)
확률을 집합으로 표현하여 연산한다.
연산 종류
- Union (합집합) - 'or'
- Intersection (교집합) - joint - 'and' / Mutally Exclusive (상호 배제 : 교집합이 공집합)
- Complements (여집합) - 'not'
- Partition - 모든 Ai 의 Union 이 Ω가 되어야 함.
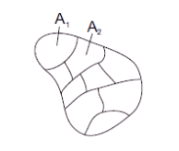
기본 연산 법칙
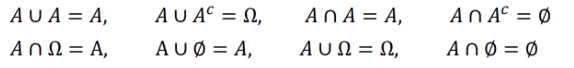
'곱하기의 항등원 : 1 -> 교집합의 항등원 : 전체집합' 처럼 +, x 등으로 치환하여 생각할 것
Ex)1. 𝐴 ∪ (𝐴 ∩ 𝐵) = 𝐴
Proof. 𝐴 + 𝐴𝐵 = 𝐴Ω + 𝐴𝐵 = 𝐴( Ω + 𝐵 )= 𝐴Ω = 𝐴
무한집합
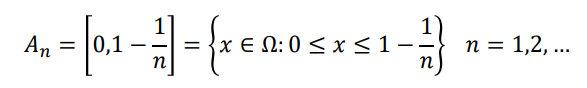
로 가정했을 때 n을 무한대로 보내면 합집합에서의 An 의 범위는 [0, 1) 즉, {𝑥 | 0 ≤ 𝑥 < 1}
반면 교집합에서 An은 0~0, 0~0.5 , .. 등과 겹치는 것은 0밖에 없으므로 {0} 이 됨
3. Probability Model
Allowable Event (Measurable Event) = Field 즉, 측정가능한 집합. (Element의 부분집합의 모임)
Sample space의 일부가 Field다? X
ex) 1~6까지의 정수가 있는 Sample space 의 부분집합 개수 2^6 개, 전체집합은 1개
즉 Ω 는 Field의 일부.
Probability Function
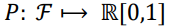
실수 0부터 1까지를 뜻함
Probability Space (확률 공간)
(Ω, ℱ, 𝑃) 가 쓰임. 확률 연산은 확률 공간에서 이뤄짐
Field 와 𝝈-field
연산을 2개에만 적용 -> Field
연산을 여러개에 적용 -> 𝝈-field
즉, 𝝈-field 는 Field의 superset이며 기본으로 공집합과 오메가를 포함함
𝝈-field 의 연산은 uncountable함. (cf : 정수는 countable infinity 실수는 uncountable infinity )
- 𝝈-field의 조건
R1) Field는 2^Ω 의 부분집합
R2) A1, A2 가 Field에 포함되면 An의 무한 합집합도 Field에 포함됨 (closed, countable, finite해야 함)
R3) 𝐴 ∈ ℱ 면 𝐴𝑐 ∈ ℱ. 즉, ℱ is closed under complementation.
(cf : 합집합의 표현 - At least one of the / 교집합 All of ~ / 여집합 Didn't ~ )
Generated 𝝈-field
가장 작은 시그마 field (즉, Minimal 시그마 field) 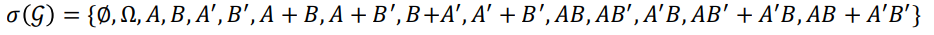
P(g) 는 Maximal 시그마 field
4. Probability axioms (3가지 조건)
- Nonnegativity (비 음수성) : For any event 𝐸, 0 ≤ 𝑃(𝐸) ≤ 1
- Additivity : Mutually Exclusive (비 동시성) 할 때 𝑃(𝐸1 ∪ 𝐸2) = 𝑃(𝐸1) + 𝑃(𝐸2).
- Normalization (일반화) : 모든 오메가의 확률은 1이다. P(Ω) = 1 <-> P(공집합) = 0
