Essential Probability Theory (2)

1. Properties of Probability measure

증명 예시 1 : 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)

A = (A∩Bc)∪(A∩B) 이고 두 항은 서로 disjoint 함 (B의 경우도 동일)
따라서 P(A) + P(B) - P(A∩B) = P(A-B) + P(B∩Ac) + P(A∩B) 이므로,
P(A U B)과 같음

증명 예시 2 : 𝑃 (𝐴𝑐) = 1 − 𝑃(𝐴)

A ∪ 𝐴𝑐 = Ω , 𝑃 (Ω) = 1 라는 규칙에 따라 (Theory (1) 참고) 성립함

2. Conditional Probability (조건부 확률)

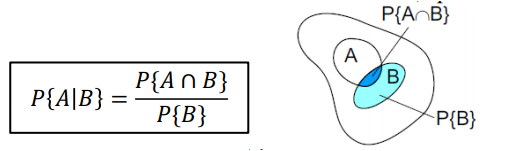
똑같은 axiom 을 만족함

• Nonegativity : Nonegative 한 A, B간의 비율이므로 음의 상태가 될 수 없음
• Normalization :
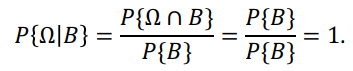
• Disjoint :

3. Two fundamental rules of probability (개념만 기억)

• Sum rule :
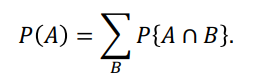
  B의 모든 경우 가짓수들을 합하면 B의 확률이 사라지고 A의 확률만 남게됨.
  (cf : P(AB) = P(A ∩ B) = P(A, B) 같은 표현)
  증명 예시 3
  
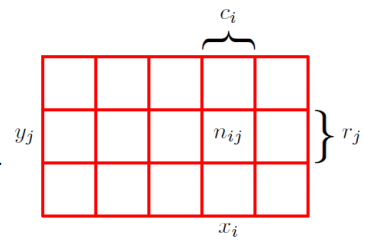
  x가 x i , y가 y j 의 값을 가질 때의 경우의 개수 = n i j
  즉, 해당 셀에 속한 점들의 개수와 같음
  이 때, P(A, B) = P(X = x i , Y = y i) 이고 N 을 모든 점의 개수로 가정하면 P(A, B) = n i j / N 가 성립 -> Y 값에 상관없이 X = x i 이므로 P(A) = c i / N
  여기서 i를 고정시키고 j 를 1 부터 변화시킨다고 생각하면
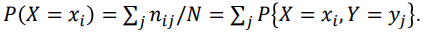  라는 식이 성립함. 이를 통해 Sum rule 이 증명된다.

• Multiplication rule
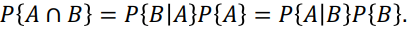  위 예시는 확률이 2개에 한할 때 성립함.
  3개일 때는 P(A, B, C) = P(B , C | A) P(A)
  P(A, B, C ,,,, ) 경우가 n개인 경우에 대한 일반식
  

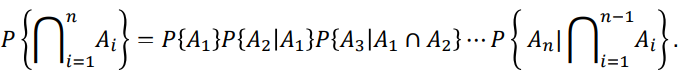
• 결론 -> Total probability rule
  위 두가지 경우를 합친 것
  

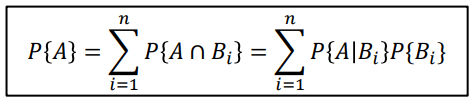
4. Bayes'rule

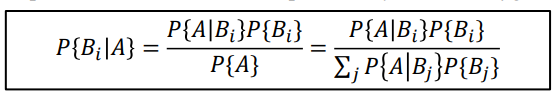P(A) 를 total rule 에 의해 바꿔서 수식으로 풀면 최종 식이 완성됨

예제 : 윗면 아랫면에 각각 색깔이 칠해진 3개의 카드가 주어져 있다. r과 b는 red, blue 를 뜻하며, 카드는 rr, bb, rb 로 구성되어 있다. 이 때 윗면이 r인 카드가 아랫면이 b일 확률을 구하라.

풀이 : P(rb | r) 을 구해야하는 상황이다. 위 수식에 대입해보기 전에 B j 의 역할을 정리해줘야하는데,
B 1 ~ B 3 를 rr, bb, rb로 가정할 수 있다. 따라서 식은 다음과 같이 정리 될 것이다.

P(r | rb)P(rb) / { P(r | rr)P(rr) + P(r |  bb)P(bb) + P(r | rb)P(rb) }

분자의 값은 rb중 r이 나올확률, 즉 1/2 과 rr, bb, rb 세 경우중 rb가 나올 확률 1/3의 곱이 된다.
분모는 1 x 1/3 + 0 x 1/3 + 1/2 x 1/3 이 되므로 답은 1/3 이다.