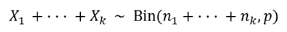10. Conditional variance and covariance
-
복습 (1) - 중요
-
복습 (2) : E(X|Y) = E(E(X|W, Y)|Y)
-
Conditional variance (조건부 분산)
-
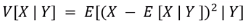
Conditional covariance
E(X) 대신 E(X|Z), E(Y) 대신 E(Y|Z) 를 치환한 식이다.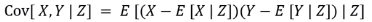
-
Conditioning rules - 이해 중요!!
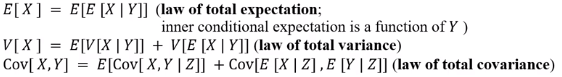
11. Proof of law of total expectation
증명보다는 11, 12, 13 법칙을 자유롭게 응용할 수 있느냐가 중요하다.
-
discrete 한 경우에 한한 증명임. (Coninuous 할 경우 Integral 을 사용해야 함)
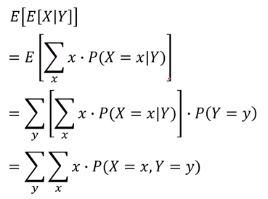기댓값 E를 sum으로 표현할 수 있음. 안에 있는 E는 X에 대한 , 바깥에 있는 E는 Y에 대한 것이다. -
finite 한 series의 경우
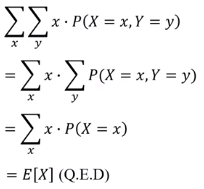
12. Proof of law of total variance
a. Variance의 정의
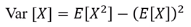
b. 첫 번째 두 번째 항을 total expectation을 이용하여 치환
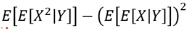
c. Variance의 정의를 이용
Var(X|Y) = E(X^2|Y) - (E(X|Y))^2 이므로
b의 첫 번째 항 내의 E(X^2|Y)에 위 식을 치환시킨다.
d. c와 유사하게 치환
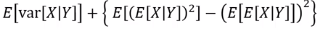
e. d와 유사하게 치환
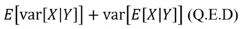
13. Proof of law of total covariance
12와 매우 유사한 방법으로 증명이 가능하다.
- cov(X,Y) = E(XY) - E(X)E(Y)
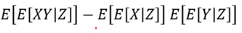치환을 이용하여 위 그림이 다음과 같음을 밝히면 된다.
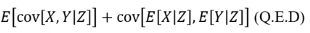
14. The distribution of max and min of independent r.v.'s (r.v = random variable)
-
Distribution of the maximum
독립인 X1 ~ Xn 들의 최댓값 : max(X1 ~ Xn)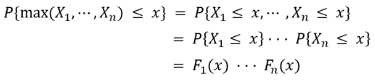
독립이므로 확률이 곱으로 표현되고 각각의 곱해진 항들은 cdf의 곱으로 나타나진다. -
Complementary distribution of the minimum
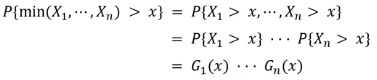마지막은 tale distribution 간 곱의 형태로 나타난다.
15. The distribution of sum of independent r.v.'s
-
가정
독립인 X, Y 이고 X + Y = Z
X의 pdf = f, Y의 pdf = g
이 때 z의 cdf = F.Z (z) 는 어떻게 구하는가?
(F.Z 는 F.X와 F.Y 의 convolution이라고 부른다) -
풀이 - 자주 쓰이는 식임
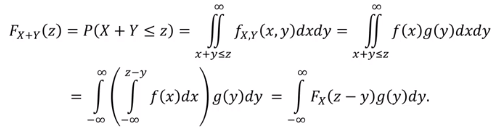중요 : 랜덤변수가 여러개가 이용될 때 (곱이든 합이든 뺄셈이든)는 joint pdf 를 사용해야 한다.
독립이므로 각각의 pdf의 곱 (f(x) * g(y)) 으로 표현되며, f(x)dx 에 대한 적분을
-무한 < x <= z-y 임을 이용하여 새로 나타낸다.
이를 계산하면 F.X 꼴의 cdf가 된다.
- pdf 구하기
위에 있는 cdf를 미분하면 pdf가 된다. (즉, F.Z (z) 를 미분한 f.Z (z) 의 값)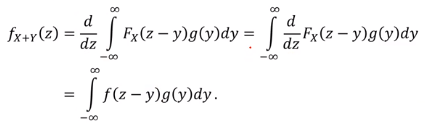
예제 : 독립 랜덤 변수 X , Y가 있는데, 두 변수는 ［0, 1］에서 uniform distribution이다.
즉 각각의 density function은 0과 1사이에서 높이가 1인 정사각형 꼴의 함수로 주어진다.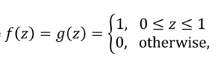
이 때 X+Y = Z 이고 pdf인 f.Z (z)를 구하라.
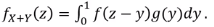
이 문제를 해결할 때는 그림을 그리는게 편하다.
i) 0 <= z <= 1 일 경우
f(z-y) * g(y) = z
ii) 1 <= z < 2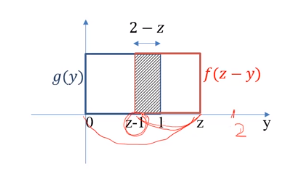
1 - (z-1) = 2-z
ii) z >= 2
f(z-y) 와 g(y)간에 겹치는 구간이 없다.
따라서 pdf는 다음과 같이 구해진다.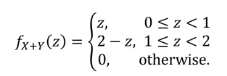 
16. Discrete Distributions
- G(z)의 정의 : Generating Function (또는 pgf : probability-genrating function)
G(z) = p.0 + p.1 z + P.2 z^2 +...
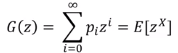기댓값의 정의에 따른 등식이다. P(X=i) 를 p.i로 표현했다.
이 때 z는 bookeeping variable이다.
{p.0,p.1, ...} 가 주어지면 G(z)를 얻을 수 있고 그 역도 성립한다.
17. Inverse transformation
G(z)가 주어졌을 때 p.i를 어떻게 구하는가?
3가지 방법이 있다.
1. G(z)를 i번 미분 * (1/i!)
이후 z=0을 대입하면 구할 수 있다.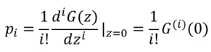 
2. partial fraction expansion 이용
= G(z)를 분해하여 부분분수로 풀 수 있다.
예제 1 : G(z) = 1/(1-z^2) = 1+z^2 + z+4 + ... 형태일 때의 p.i를 구하라.
a/(1-r) = a + a*r + a*r^2 + ... 과 같은
무한 급수의 형태이다.
따라서 i가 짝수일 때는 계수가 1이므로 1,
i가 홀수일 때는 계수가 0이므로 0이다.예제 2 :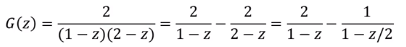 
(풀이가 포함되어 있음)
모든 항들을 무한급수 꼴로 만들기 위해 2-z는 1-z/2 로 바꿔야한다.
A(1-a*z) 는 A*a^i 꼴의 sequence로 나타나므로
p.i = 2*(1)^i - 1*(1/2)^i = 2-(1/2)^i3. path integral 이용 - 1, 2에 비해 중요하지 않음
18. Calculating the moments with aid of G(z)
- 복습 : E(X^n) = n차(order) moment
n차 moment는 G(z)를 미분하여 구할 수 있다.
G(1) 은 G(z)의 정의에 의하여 1이 되므로
G'(z) = E(X* z^(x-1))
G'(1) = E(x) 이 되며
미분을 여러번할 경우 다음과 같은 등식이 성립한다.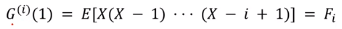
F.i 는 factorial moment라고 한다.
그러나 위와 같은 방식으로는 E(X(X-1)) 꼴의 경우를 구할 때 쓰이며, E(X^2) 와 같은 ordinary moment를 구하기 위해서는 19와 같은 변환 관계를 알아야한다.
19. The relation between factorial and ordinary moment
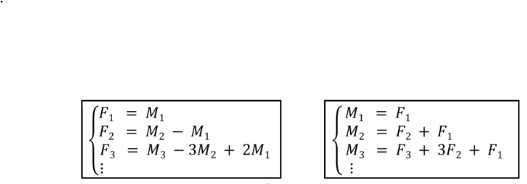
예시 : F.2 = G''(1) = E(X(X-1)) = E(X^2) - E(X)
-> M.2 = E(X^2) = F.2 + F.1 = G''(1) + G'(1)
-> V(X) = M.2 - (M.1)^2
20. Direct calculation of the moment
변환 관계를 거치지 않고 바로 구하는 방법 (|z=1 은 z에 1을 대입하라는 의미)
G'(z)|z=1 는 E(X* z^(X-1))|z=1 = E(X)
마찬가지로 2번 미분하는 경우는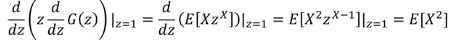
이를 일반화 하면 다음과 같다.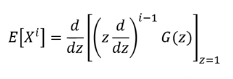
21. Generating function of the sum of independent r.v.'s
독립인 랜덤변수 X와 Y가 있고 X+Y에 관심이 있다. 이에 대한 pgf를 구하려면?
X+Y=Z라 가정하자.
G.Z (z) = E(z^(X+Y)) = E(z^X ＊ z^Y)
= E(z^X)＊ E(z^Y) = G.X (z)* G.Y (z)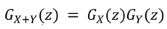
p.i = P(X=i ; X가 i가 될 확률) , q.j = P(Y=j)라 가정하자.
이 때 X+Y의 distribution 즉, P{X+Y =k} 는
다음과 같이 p와 q의 convolution으로 표현된다.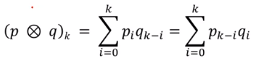 
연속적일 경우 convolution의 정의 처럼 Integeral 로 표현되지만 discrete하므로 위와 같이 합성곱의 형태로 나타난다.
pgf의 곱의 형태로 나타낸 뒤 역으로 뽑는 것이 낫다. -중요
22. Compound distribution and its generating function
랜덤 변수 X.i 들을 random sum 한 것을 Y라고 가정하자.
(Y = X.1 + X.2 + ... + X.N , 이 때 N은 랜덤 변수)
각각의 pgf 를 구하면,
G.X (z) , G.N (z) 이고
우리가 원하는 것은 G.Y (z) 이므로
4번째 줄의 E(z~ | N)에서 앞의 term은 상수화가 됨을 유의해야 한다. 또한 G.N(z) = E(z^n) 이므로 5번째와 같은 표현이 성립한다.
23. Bernoulli distribution (베르누이 분포)
X = 1 or 0 이라고 할 때 1이 될 확률은 p, 0이 될 확률은 q = 1-p 이다.
예제 : G(z) = P(X=0) * z^0 + P(X=1) z^1 = q + pz
이는 앞서 언급한 공식을 이용해
E(X) = G'(1) = p
V(X) = G''(1) + G'(1)(1-G'(1)) = p(1-p) = pq
로 표현할 수 있다.
24. Binomial distribution X ~ Bin(n, p)
동전의 앞(또는 뒷)면이 나온 횟수가 몇 번인가?
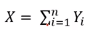
n=1 일 경우 pgf는 (q+pz) 이고 n번 동전을 던지면 (q + pz)^n 이다. (independent 하므로)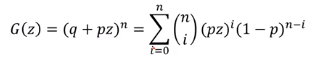
= 
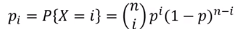
마찬가지로 이를 통해 E(X)와 V(X)를 구할 수 있다.
독립시행이므로 n배를 해주면
E(X) = nE(Y.i) = np
V(X) = nV(Y.i) = np(1 - p)
- 확장 : 보아송 분포 (Poisson random variable)
포이즌?
np 가 일정할 때 (즉 상수일 때) 시행을 무한 반복(n -> 무한) 하면 p->0 (무한소) 이 된다.
이를 표현하면 np = λ (poisson rate)복습 : e^x = lim(n->무한) (1+ x/n)^n = 무한시그마 (x^n)/n!
G(z) = (1 - p + pz)^n
이때 p = λ/n 이므로
(1 - (1-z) * λ/n )^n
위의 복습 부분에 있는 정의를 이용하면
(1-z) * λ 가 x에 해당되므로
exp(-(1-z) * λ) 가 된다.25. The sum of Bionomially ditributed random variables
동일한 확률값 p를 가질 때, 여러 binomial 분포를 합할 때는 횟수 n 들만 합해주면 된다.
