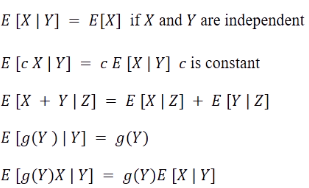Random Variables and Distributions (1)

준덕이·2020년 5월 3일

data statistics

기술 통계학 길라잡이

목록 보기

5/6

1. Random variables(확률 변수) and Distributions

확률 변수 = 일종의 함수임 : X(e)
셀 수 있는 경우의 값을 가질 때 : 이산 확률 변수
실수의 값을 가질 때 : 연속 확률 변수

Sample space의 임의의 부분집합 e 에 assign 된 값 = 함수값 : X(e)
함수 X는 Sample space 를 실수(R)로 Mapping 해준다.

예제 2 : 동전을 연속으로 3번 던져서 head 가 나올 경우의 수는?

X를 head의 개수로 가정하면
e = hhh 일 경우 X(e) = 3 
e = hht -> X(e) = 2
e = htt -> X(e) = 1
...

image = 함수 결과 값의 범위 (오메가 x)
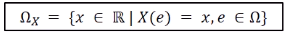
정의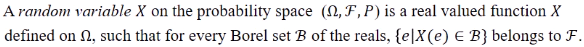(Borel set : 위상 수학(topology)에서 현재 우리가 사는 공간은 유클리드 공간이다. 3차원에서의 measure는 공간이다.) : 랜덤변수는 특정 event에 실수값을 assign 해서 얻은 값들이다.

note 1) 콜렉션 C.I 의 요소들 : (a,b] , (-무한, b], (a, 무한) 로 구성되는 interval type에 measure을 assign 한다고 가정하자.
-> 여기서 measure인 u(I) 는 b-a, 무한, 무한 으로 표현되는 길이가 있다. 소괄호가 포함되어 있으므로 open interval 에 해당하며, open interval 로 이뤄진 집합은 field가 될 수 없다. 즉 C.I는 field가 되지 못한다.

field 의 특징 : intersection 을 하든 union, complement를 하든 필드에 그대로 남아야한다.

note 2) C.F : C.I 의 요소를 답보하고 있지만 disjoint 한 경우 겹치지 않기 때문에 field가 될 수 있다.
-> disjoint 할 때는 measure들이 a~ x, 까지 길이 x~b 까지 길이를 합치는 union이 된다.

note 3) C.F도 한쪽 끝이 극한으로 갈 경우 연산이 닫히지 않는 경우가 생긴다.
-> C.F가 만들어내는 generated sigma field (가장 smallest 한 field) : σ(C.F)
또는 Borel set이라고 한다. (주로 B로 언급됨)

2. Conitnuous random variable (연속 확률 변수)

Distribution function (일명 cdf 라고 불리며, 단조 증가 함수이다.)
F(x) = P{ X <= x }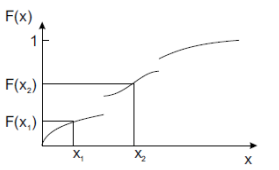 interval 값 : P{ x1 < X <= x2 } = F(x2) - F(x1)
Complementary distribution function (tail distribution)
G(x) = 1 - F(x) = P{ X > x }(x= 무한대 일 때 0으로 수렴한다)
Probability density function (pdf : cdf 를 미분한 것이다.) 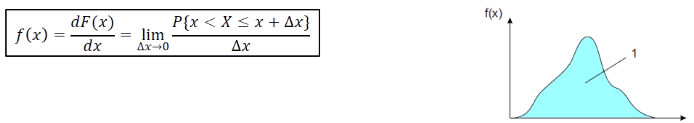적분 값은 1이다.

3. Discrete random variable (이산 확률 변수)

cdf
p.i = P{ X = x.i } = F(x.i) - F(x.i - : 왼쪽에서 수렴했을 때)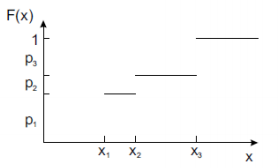 위 뺄셈의 값은 아래 그림에서의 확률 값이 된다.

Probability mass faunction (pmf)x.i 는 질량값 즉, 확률값을 의미한다. 여기서 막대기 3개의 합은 1이된다.

4. Joint random variables and their distributions

Joint distribution function
F.X.Y (x, y) = P{ X <= x, Y <= y }
(F.X.Y는 그냥 F로 표현되는 경우도 많음)
랜덤 변수 X, Y 가 각각 x, y 보다 작거나 같을 경우
Joint probability density function (joint pdf : 위에거 미분한 거)
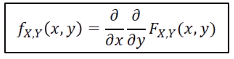
Independence : 독립일 경우 joint pdf 는 곱으로 표현된다.
F.X.Y (x, y) = F.X(x) * F.Y(y)

5. Function of a random variable

랜덤 변수의 cdf 나 pdf 를 구하는 것이 관건이다.
Y = g(X) 일 때, Y<=y 일 값을 구하라.

g(X) <= y <-> X <= g(y) 역함수
F.Y (y) = F.X (g(y) 역함수)

image [0, 1] 에서 g(*) = F.X (*) 라고 가정하면
F.Y (y) = F.X ( F.X (y) 역함수) = y 이고
양변에 미분을 취하면 f.Y(y) = d*F.Y (y) / dy = 1 이다.
그래프로는 변이 1인 정사각형으로 나타난다.

Y는 uniform distribution (일명 U) 분포를 가진다.
Y = F.X (X) ~ U : Y is distributed by uniform 
이 때 양변에 역함수를 취해주면
X ~ F.X(U) 역함수 이다.

X ~ F.X(U) 를 통해서 F of X (F.X)의 분포를 갖는 랜덤 변수를 생성할 수 있다.
C언어에서 rand() 함수의 역할을 수행한다고 볼 수 있다.

6. Generating a random variable using uniform r.v.

U라는 uniform 랜덤 변수가 있다고 가정하면, H라는 distribution 함수를 갖는 랜덤 변수 X 는 어떻게 생성하는 가?
-> X = H(U) 역함수
증명 : F.X(x) = H(x) 임을 보여야 한다.
F.X(x) = P(X<=x) = P(H(U) 역함수 <= x)
H가 monotone increasing (단조 증가) 일 때만 a<=b -> H(a)<=H(b) 가 성립한다.
따라서 F.X(x) = P{ H(H(U) 역함수) <= H(x)}
.= P{U<= H(x)} = H(x)

예제1 : 분포가 F.X(x) = x^n 이고 0 < x < 1 인 랜덤 변수 X를 생성하려면?

x = F.X(u) 역함수 라 가정하면,
u = F.X(x) = x^n 또는 x = u^(1/n) 이다.
따라서 X= U^(1/n) 으로 설정하여 X를 생성할 수 있다.

예제2 : F.X(x) = 1 - e^(-ax) 인 지수분포를 가질 경우

x = F.X(u) 역함수
u = F.X(x) = 1 - e^(-ax) 또는 x = -(1/a)ln(1-u)
X = F.X(U) 역함수 = -(1/a)ln(1-U)

이때 uniform 의 범위가 [0, 1] 이므로
ln(U) 여도 상관 없다.

7. The pdf of a conditional distribution

정의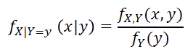P(A|B) = P(A, B)/P(B) 와 동일한 경우라고 할 수 있다.
Y의 marginal(joint 와 반대) distriution = f.Y(y) = 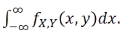위 경우에서 분모에 해당함
정의식의 양변에 dx 를 곱해서 면적화 한다. (pdf화)

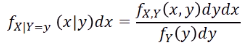
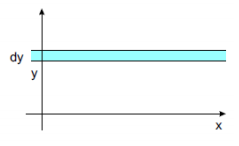띠의 면적이 분모의 값(Y=y 일 확률에 해당), 분자는 x~ dx 에 해당하는 띠의 면적이다.

8. Parameters of distributions

-기댓값(Expectation)-

Continuous distribution :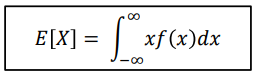P(X=x) 가 f(x)dx 에 해당한다.
Discrete distribution :
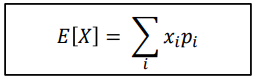
일반적으로 Conitnuous distribution 에서 dF(x) 는 dx (interval) 의 확률이다.

-Properties of expectation-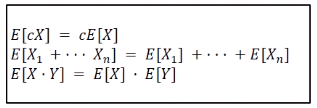랜덤변수 X에 E함수를 적용시키면 Constant (위 그림에서 c)가 된다. 첫번째 두번째 성질은 선형성(linear)을 의미한다. 즉 E는 linear operator이다. 그러나 세번째 성질은 X와 Y가 독립인 경우에만 성립한다. (즉 linearity 판별에는 무관)

-분산(Variance) 또는 에러?-
변하는 값의 중심값 : 평균값
평균값과 변하는 값 사이의 거리를 제곱한 것 = 분산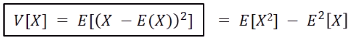제곱을 왜 하느냐? -> E(X - E(X) ) = E(x) - E(X) = 0
X가 상수면 당연히 0이다. E(X^2) = X^2 이기 때문.

-Covariance-
랜덤변수가 2개 이상일 때 부터 적용 가능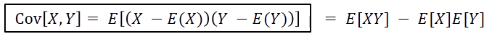Y가 X일 때 두 변수 사이의 Covariance는 Variance 값과 동일하다. 또한 Covariance 역시 Variance와 마찬가지로 order(승)가 2인 operator이다.

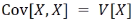
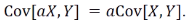여기서 a는 임의의 상수이다. 또한 X와 Y가 독립이면 Cov(X,Y) = 0이 성립한다.

-Properties of variance-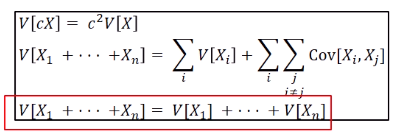첫번째를 보면 c는 Cov와 달리 제곱하여 나온다. 세번째는 Expectation의 특징과 유사하나, X_i 들이 모두 독립인 경우에만 성립하며 보통은 두번째 등식을 따른다.

-Properties of covariance-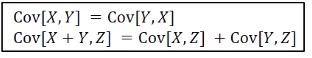교환법칙, 분배법칙과 유사하다.

9. Conditional expectation(조건부 기댓값) - <매우중요>

P와 마찬가지로 E역시 E(X|Y) 꼴로 조건식을 넣을 수 있다. (Y=y로 고정되어있다는 조건 하에)일반적인 E(X)의 정의에서 dF(x) 대신 conditional pdf 를 곱한 것 외에는 차이가 없다.

E(X|Y=y) 는 Y가 상수, 즉 랜덤변수가 1개인 상황이다.
E(X|Y) 는 2개이나 아무 말이 없을 때는 E가 X(앞에 있는 변수)에 관한 기댓값임을 의미한다.
반면 E(E(X|Y)) 에서 바깥에 있는 E는 Y의 기댓값을 의미한다. 왜냐하면 E 연산자는 대상의 랜덤변수 성질을 죽여버리는(즉, 상수화 시키는) 역할을 수행하기 때문이다. 따라서 내부의 E에 의해 괄호 안에는 Y의 랜덤변수 성질만 남는다.

Total expectation rule (Total probability rule과 마찬가지로 X의 기댓값을 바로 구하기 힘들경우 쓰인다.)
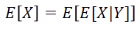
이와 동일한 식은 아래와 같다. (조건부 기댓값의 정의를 대입한 것)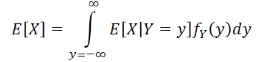
이와 같은 방식으로 E(X|Y=y) 도 유도할 수 있다.
2번째 식에서 y를 w로 치환하면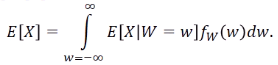이고
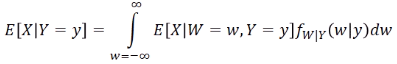가 된다. - 자주쓰임