SL Foundation
- Supervised Learning (지도학습)
Given a set of labeled examples (x, y), learn a mapping function g: X→Y
- learning from data
- Learning model procedures
: Feature selection → Model selection → Optimization
- Classification & Regression
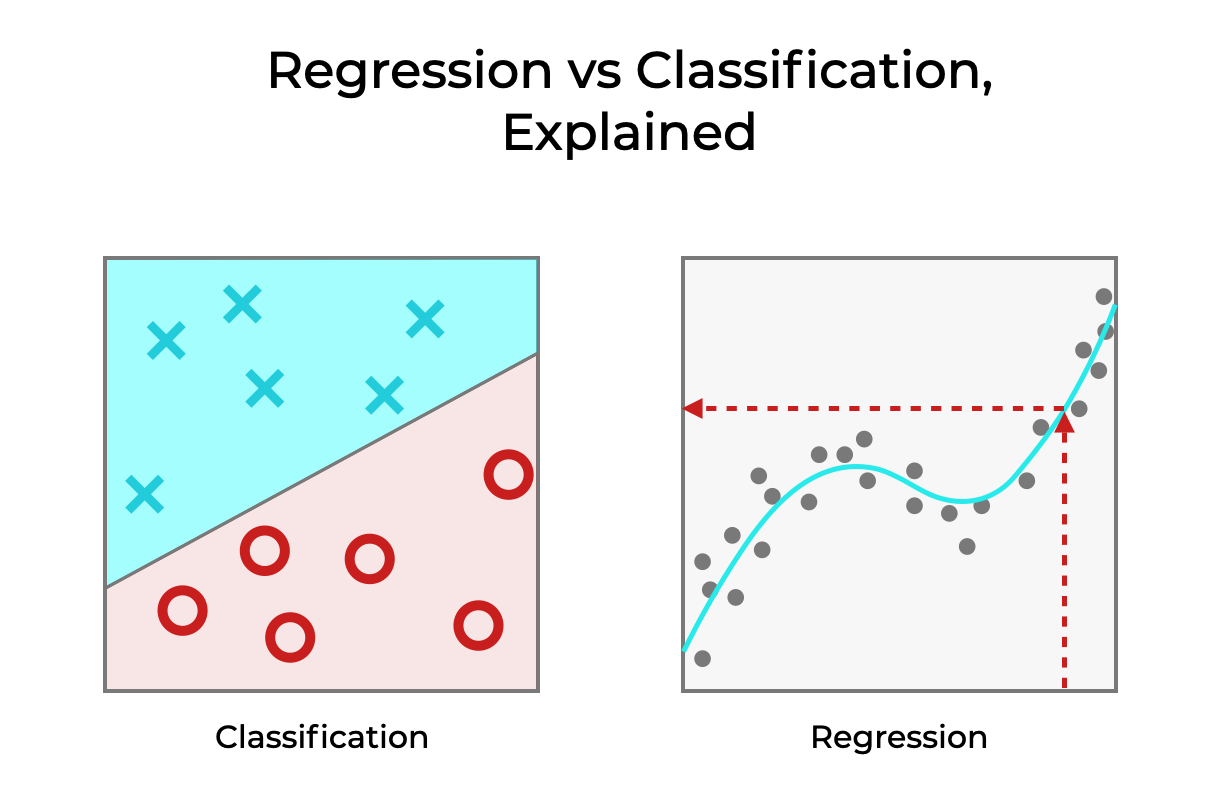
-
Model "generalization" is a goal (to perform well on the unseen data)
- to minimize the Generalization error (E gen)
- Learning from data → Learning from error
-
Training error (E train)
-
Testing error (E test) can be a proxy for E gen
-
Curse of dimension: as the input data or feature dimension increases, the number of sample data should exponentially increases, which is impossible in real.
-
to avoid Overfitting, we can use:
- Data augmentation
- Regularization
- Ensemble
-
Cross validation (CV)
- K-fold cross validation
: one fold is used as "validation" dataset (to avoid overfitting)
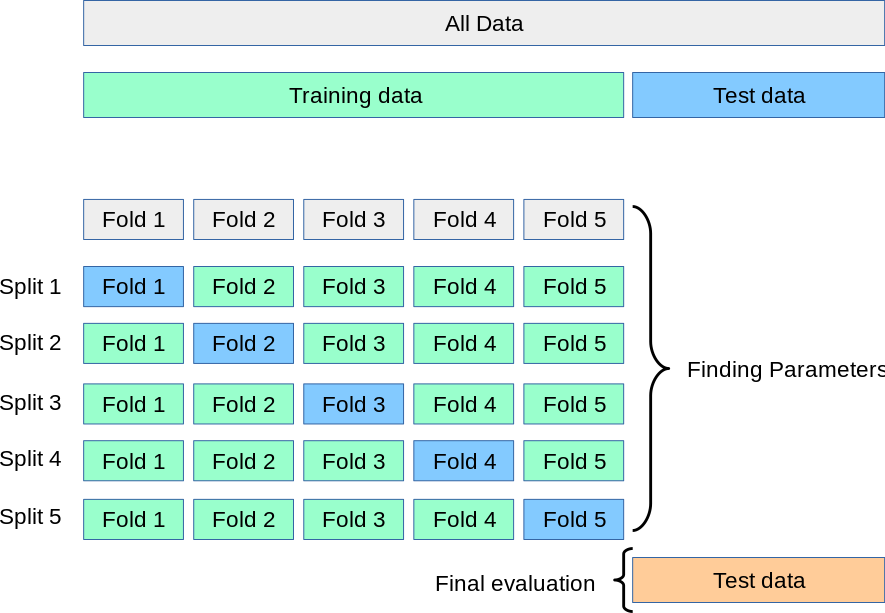
- K-fold cross validation
Linear Regression
-
Linear models
- Θ: model parameters
- x: features
- good for a first try
-
Univariate problem when the output is determined by a single feature, Multivariate problem when the output is determined by multiple features
-
Linear regression framework
- Choose Hypothesis class
- Loss function: to minimize MSE
- Determine Optimization algorithm
-
Iterative optimization by Gradient descent
-
Gradient: the derivative of vector functions, direction of greatest increase/decrease of a function
-
which direction? steepest gradient descent with a greedy method
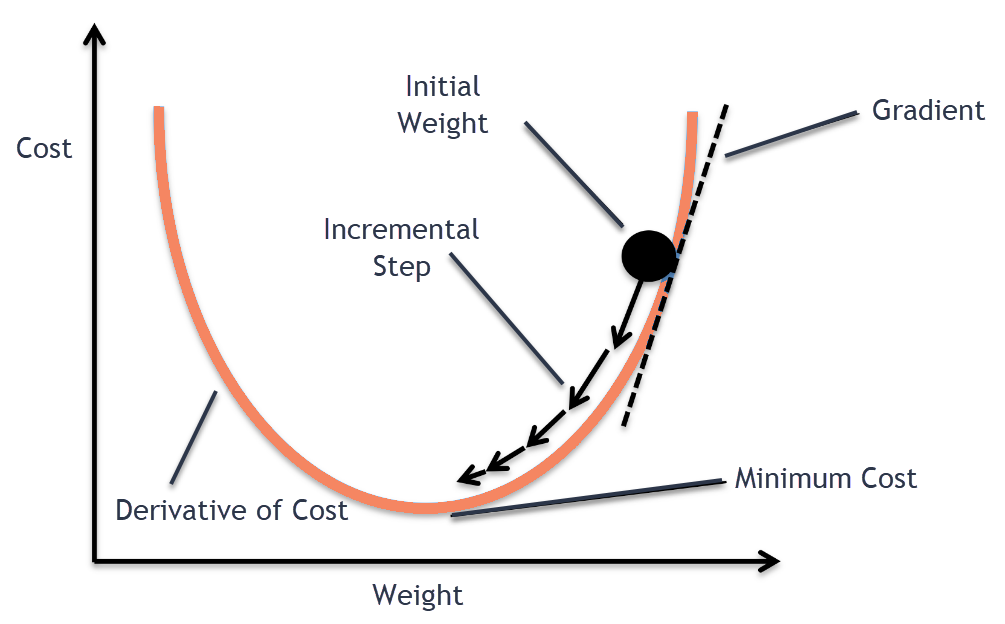
c.f. Error surface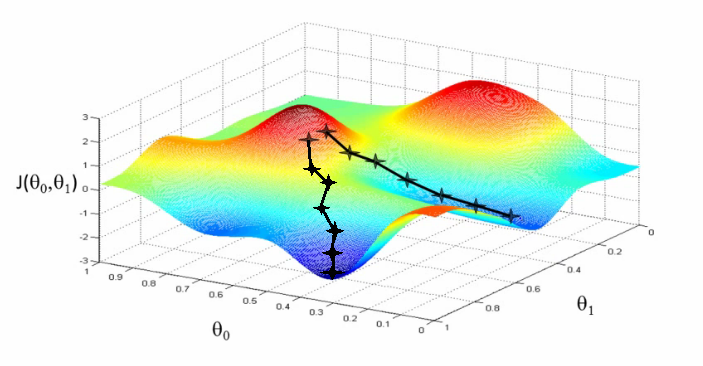
-
works well even when the number of samples is large
-
Gradient Descent
-
Stochastic Gradient Descent (SGD)
- Unlike Batch Gradient Descent which needs to iterate m times for one step, SGD is a mini-batch type
- Limitation: reach local optimum, not global optimum
-
To avoid local optimum:
- Method of Momentum
- 과거에 gradient가 update되던 방향 및 속도를 반영하여 현재 포인트에서 gradient가 0이라도 계속 학습이 진행될 수 있다.
- Nesterov Momentum
- difference: gradient is evaluated (lookahead gradient step)
- AdaGrad
- adapts an individual learning rate of each direction
- limitation: gradient is accumulated and this leads to learning rate's decrease, which means the algorithm is no longer able to learn
- RMSProp
- attempts to fix AdaGrad
- Adam
- Adaptive Moment Estimation
- RMSProp + momentum
- Method of Momentum
-
Learning rate scheduling
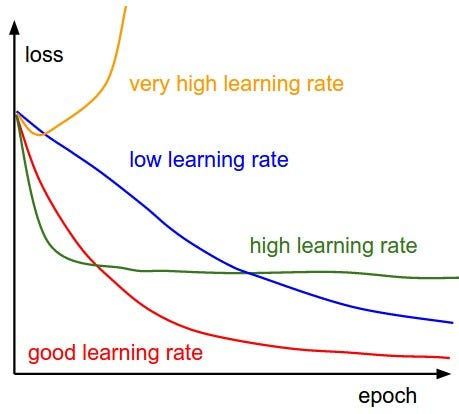
-
to avoid overfitting, "Regularization"
- keep the features but reduce magnitude/valudes of parameters
Linear Classification
-
Linear classification Hypothesis H
- w: model parameter
- x: feature
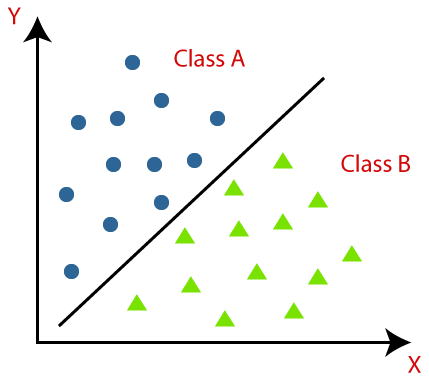
- Hyperplane (Decision Boundary)
- Binary decision(output): yes/no
-
Linear Classification Framework
- Choose Hypothesis class
- Loss function: Zero-one loss, HInge loss, Cross-entropy loss
- Optimization algorithm: Gradient Descent algorithm
-
Score and Margin
-
Sigmoid function: score and probability mapping
-
Multiclass classification
- One-VS-All: use multiple binary classifications to perform multiclass classification
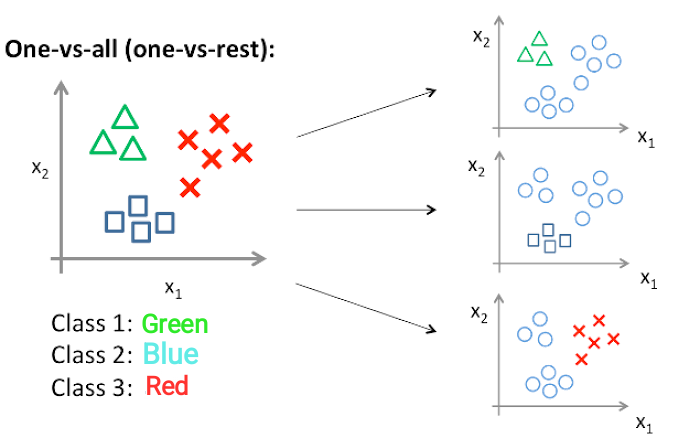
- one hot encoding된 label값과 sigmoid model이 출력하는 확률값을 비교해서 loss function을 통해 error 계산하고 학습
- One-VS-All: use multiple binary classifications to perform multiclass classification
Advanced Classification
-
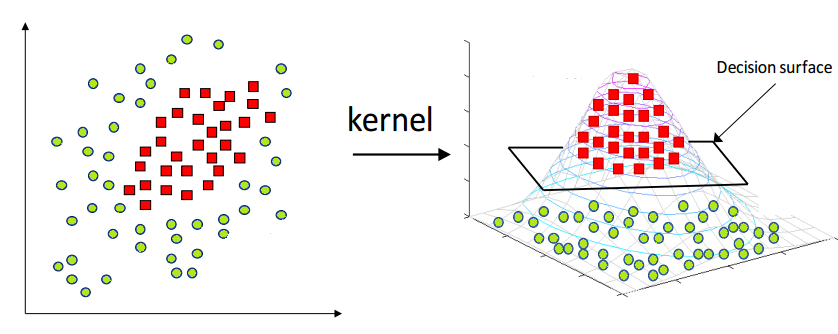
Support Vector Machine (SVM)
- chosse the hyperplane with th largest margin on either side
- when data samples are not linearly separable, we can use Kernel Trick
-
Artificial Neural Network (ANN)
- non-linear classification model
- basis of Deep Neural Network
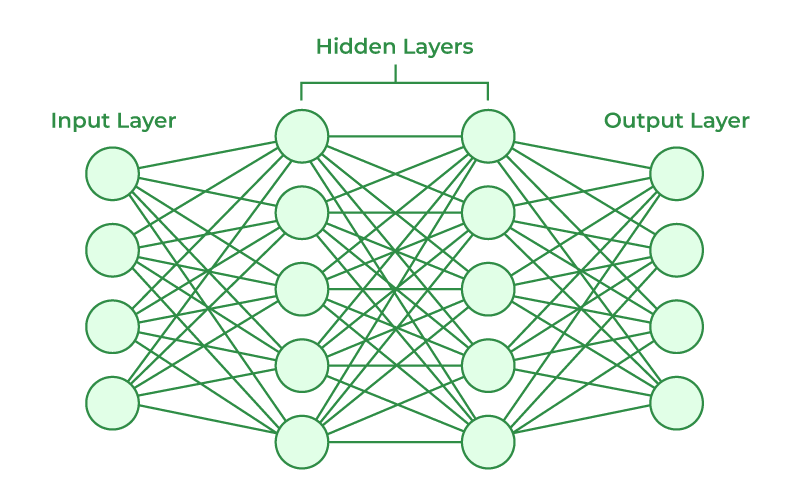
- Multilayer perceptron: can solve XOR problem
- Gradient Vanishing problem: low accuracy even when the # of layers is high
- Backpropagation
- barely changes lower-layer parameters
-
Convolutional Neural Network
: classification model for high-demensional data
Ensemble
머신러닝 알고리즘의 종류에 상관없이 서로 다르거나 같은 매커니즘으로 동작하는 다양한 ML 모델들을 묶어 함께 사용하는 방식
-
(+) can improve predictive performance, and do not need too much parameter tuning
-
Bagging and Boosting
- Bagging
- Bootstraping + Aggregating
= Generate multiple random datasets from original dataset & Train each model in parallel & Aggregate
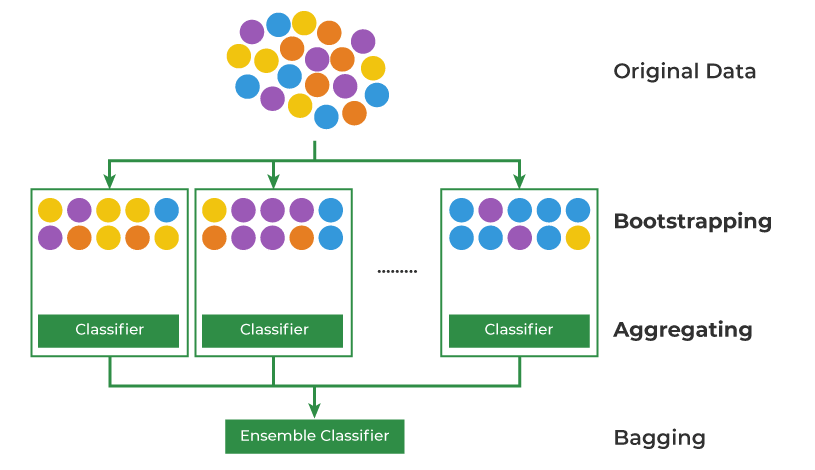
- Bootstraping + Aggregating
- Boosting
- cascading of weak classifiers (that have high bias, which means a single classifier cannot work alone)
- e.g. AdaBoost: trained on weighted form of the training set
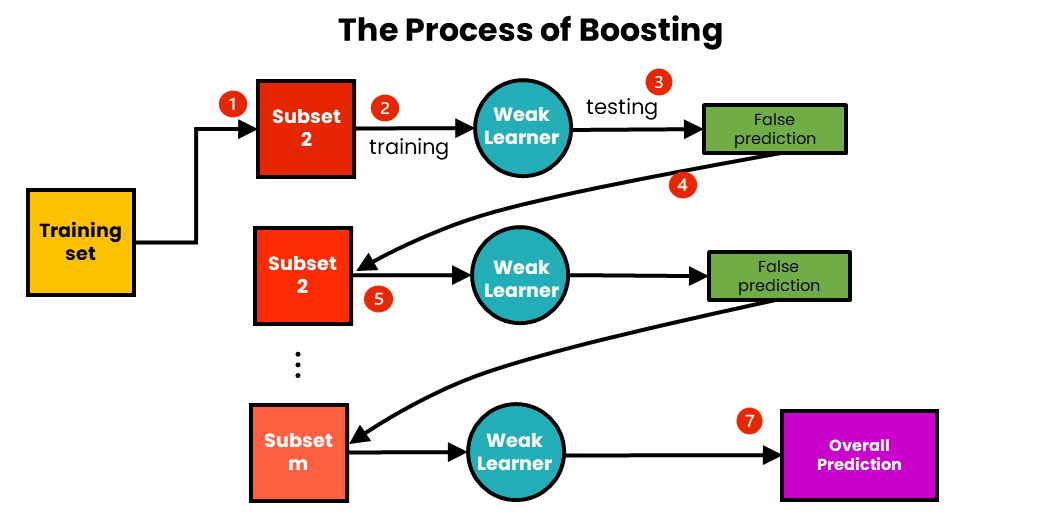
- Bagging
-
Performace Evaluation in SL
- Accuracy
- Confusion matrix
- False positive/negative error
- Precision
- Recall
- ROC curve: 서로 다른 classifiers의 성능 측정 시 사용