트리(Tree)
서로 연결된 Node의 계층형 자료구조로써, root와 부모-자식 관계의 subtree로 구성되어 있다.
root에서 시작하여 여러 개의 tree가 중첩되는 형태로 만들어진다. 하나의 tree안에 여러 개의 subtree가 존재한다.
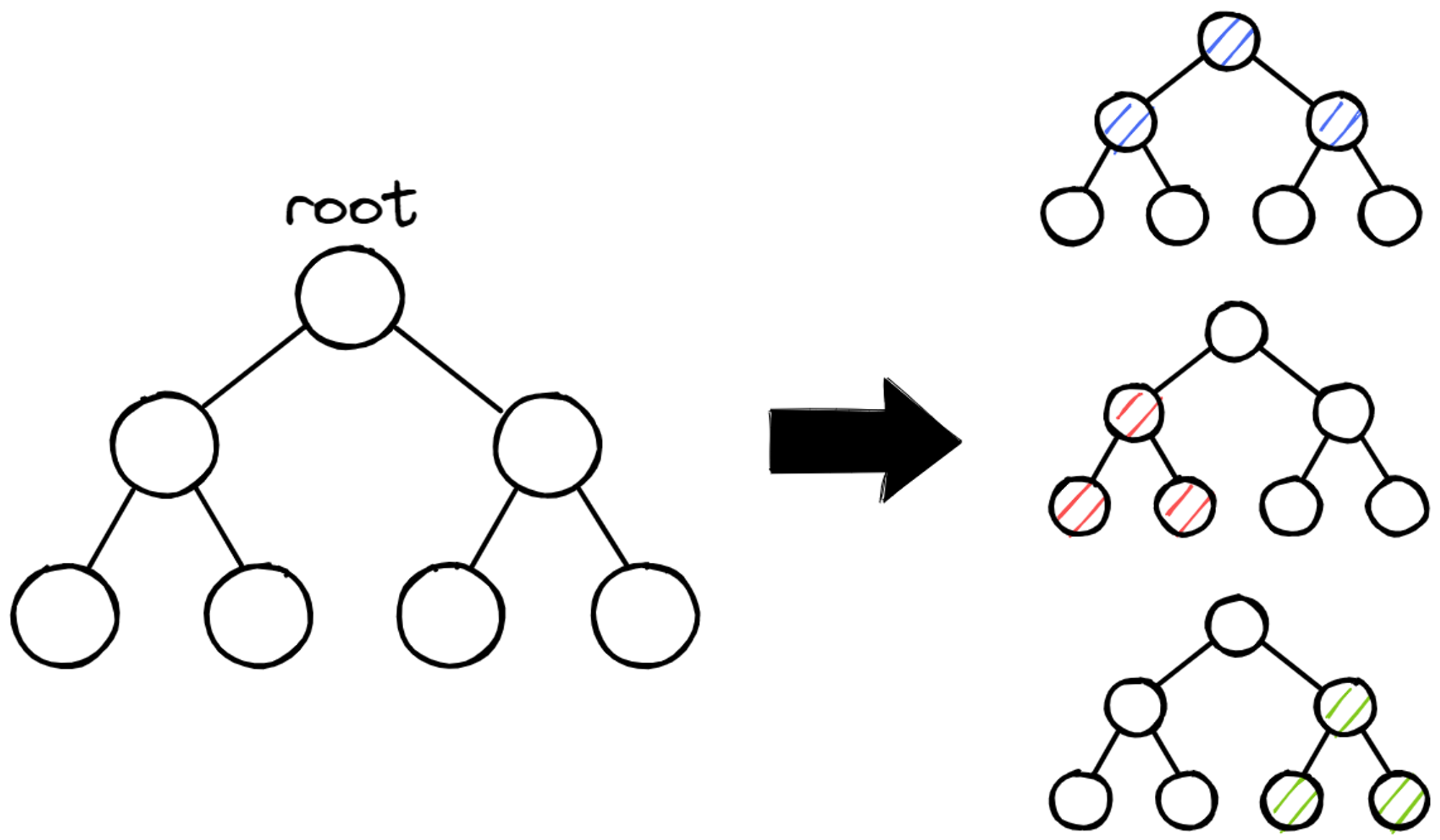
Tree 관련 개념
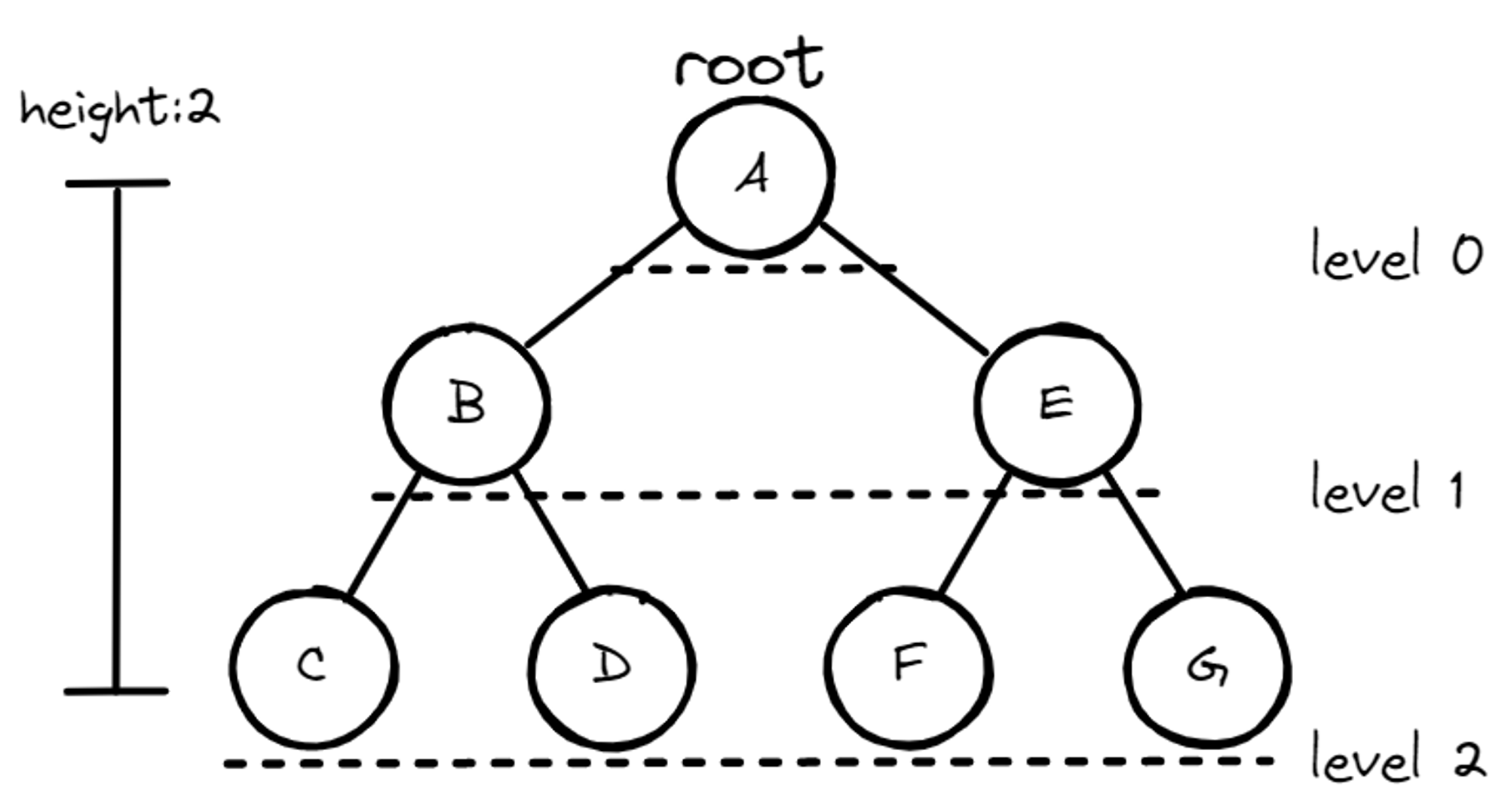
- 정점(Vertex): A, B, C와 같은 값을 갖고 나타내며, 노드로 표현한다.
- 간선(Edge): 정점 간에 연결된 선이다.
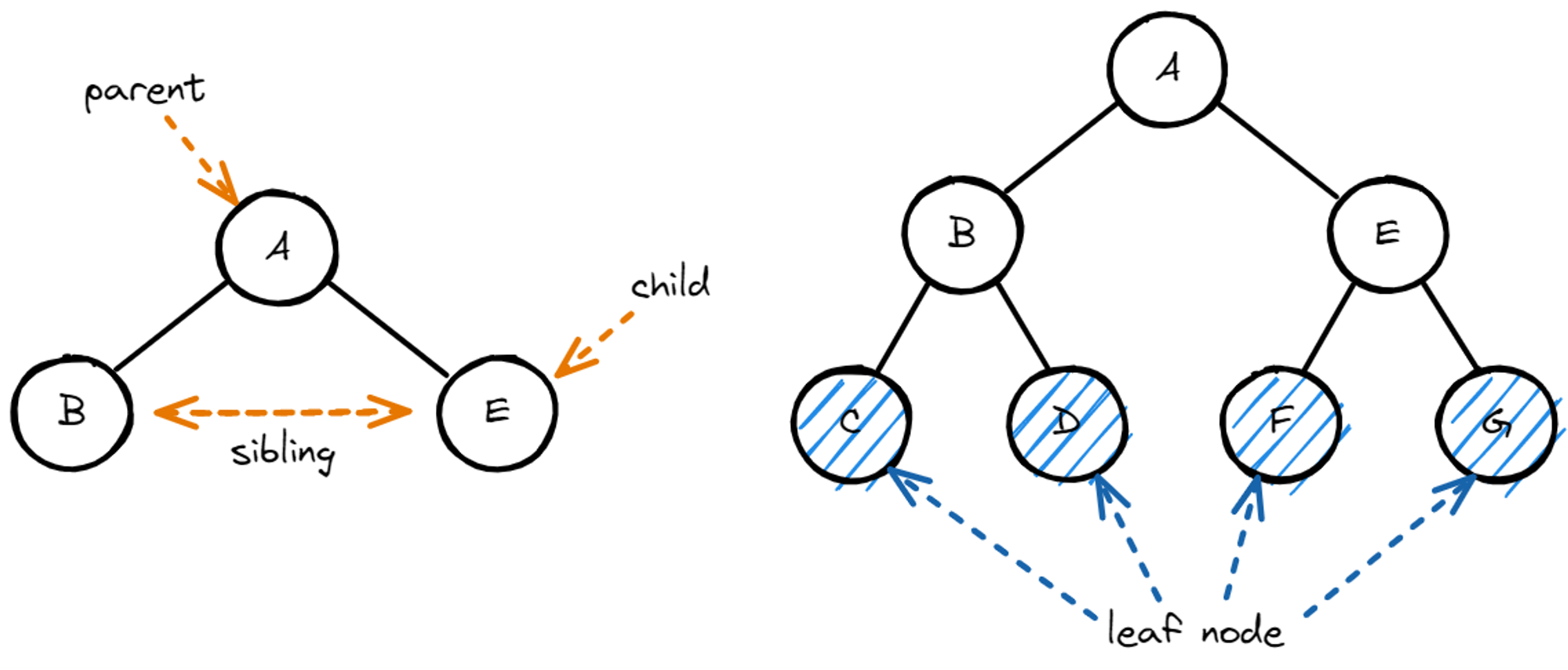
- 자식 노드(Child), 부모 노드(Parent)
- 형제 노드(Sibling): 같은 부모를 가진 노드를 말한다.
- 리프 노드(Leaf): 더 이상 뻗어날갈 수 없는 마지막 노드를 말한다.
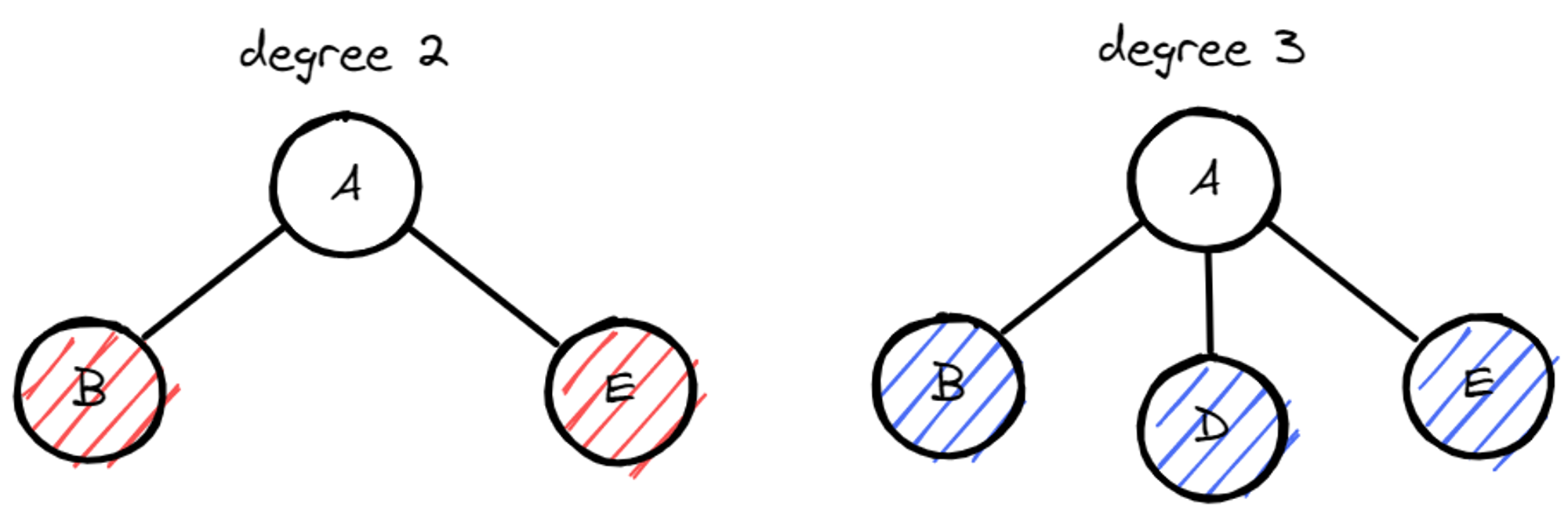
- 차수(Degree): 각 노드가 갖는 자식의 수, 모든 노드의 차수가 n개 이하인 트리를 n진 트리라고 한다.
- 조상(Ancestor): 위쪽으로 간선을 따라가면 만나는 노드를 말한다.
- 자손(Descendant): 아래쪽으로 간선을 따라가면 만나는 노드를 말한다.
- 루트 노드(Root): 트리의 시작점이다.
- 높이(Height): 루트 노드에서 가장 멀리있는 리프 노드까지의 거리이다.
- 레벨(Level): 루트 노드에서 떨어진 거리이다.
트리 순회
선형 자료구조인 배열과 리스트의 경우, 순회하는 법이 인덱스 0, 1, 2부터 n-1까지로 방법이 정해져있다.
하지만 트리는 비선형 자료구조이기에 순회하는 방법이 여러가지 존재한다. 아래가 대표적인 방법들이다.
- Level Order Traversal
- Preorder Traversal
- Inorder Traversal
- Postorder Traversal
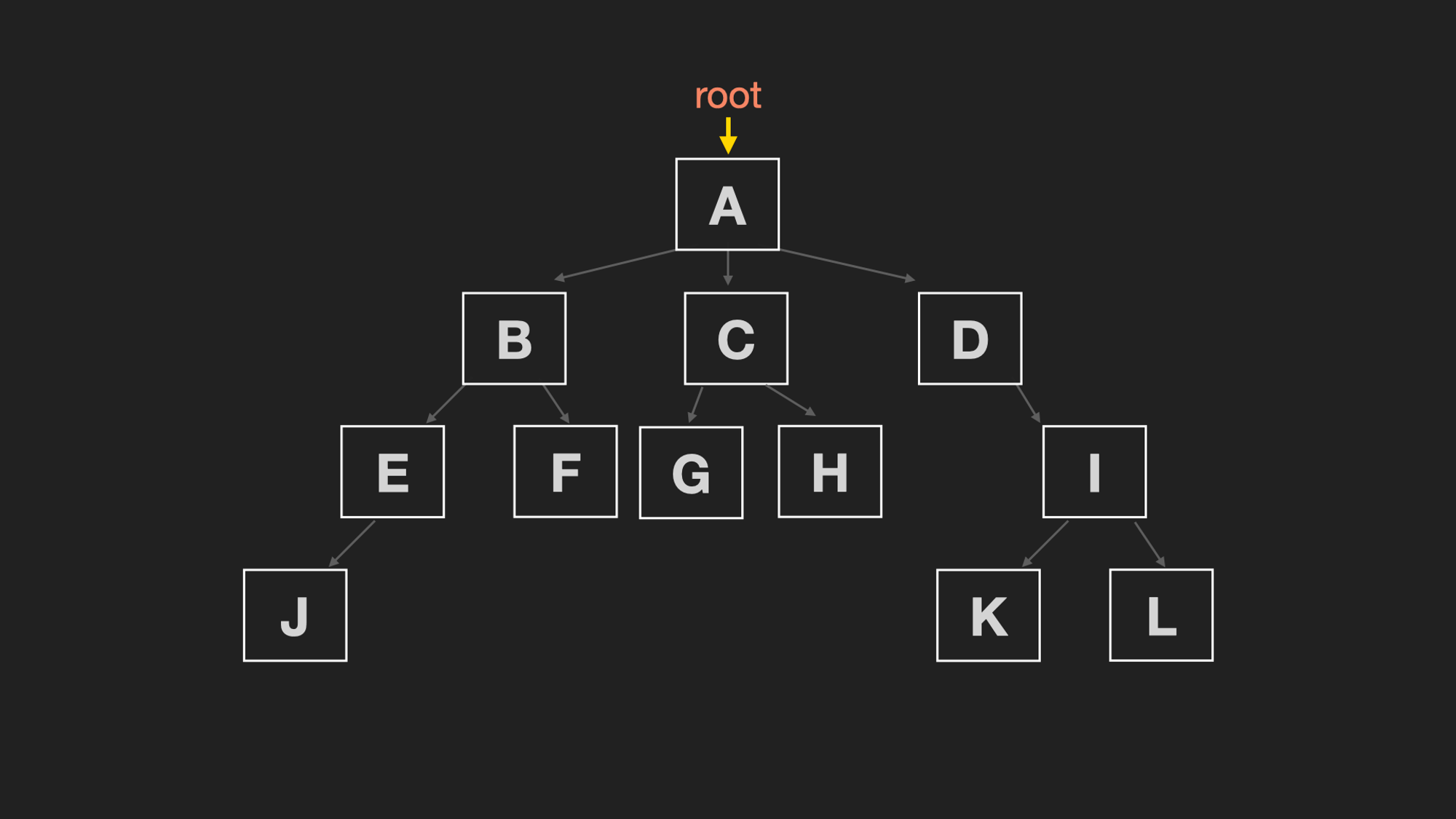
Level Order Traversal
Level Order Traversal는 말 그대로 level 별로 순회하는 것을 말한다.
(A) ⇒ (B, C, D) ⇒ (E, F, G, H, I) ⇒ (J, K, L)
- level0: A
- level1: B, C, D
- level2: E, F, G, H, I
- level3: J, K, L
Level Order Traversal의 시간 복잡도
모든 정점의 개수가 n에 대해,
shift()하고push()하는 과정이 n번 일어남으로 O(n)의 시간복잡도를 갖는다.
전위순회(Preorder), 중위순회(Inorder), 후위순회(Postorder)
트리에서의 순회는 트리를 돌아다니는 것이고, 방문은 노드의 값을 접근하는 것(출력, 저장 등의 행위)이다.
-
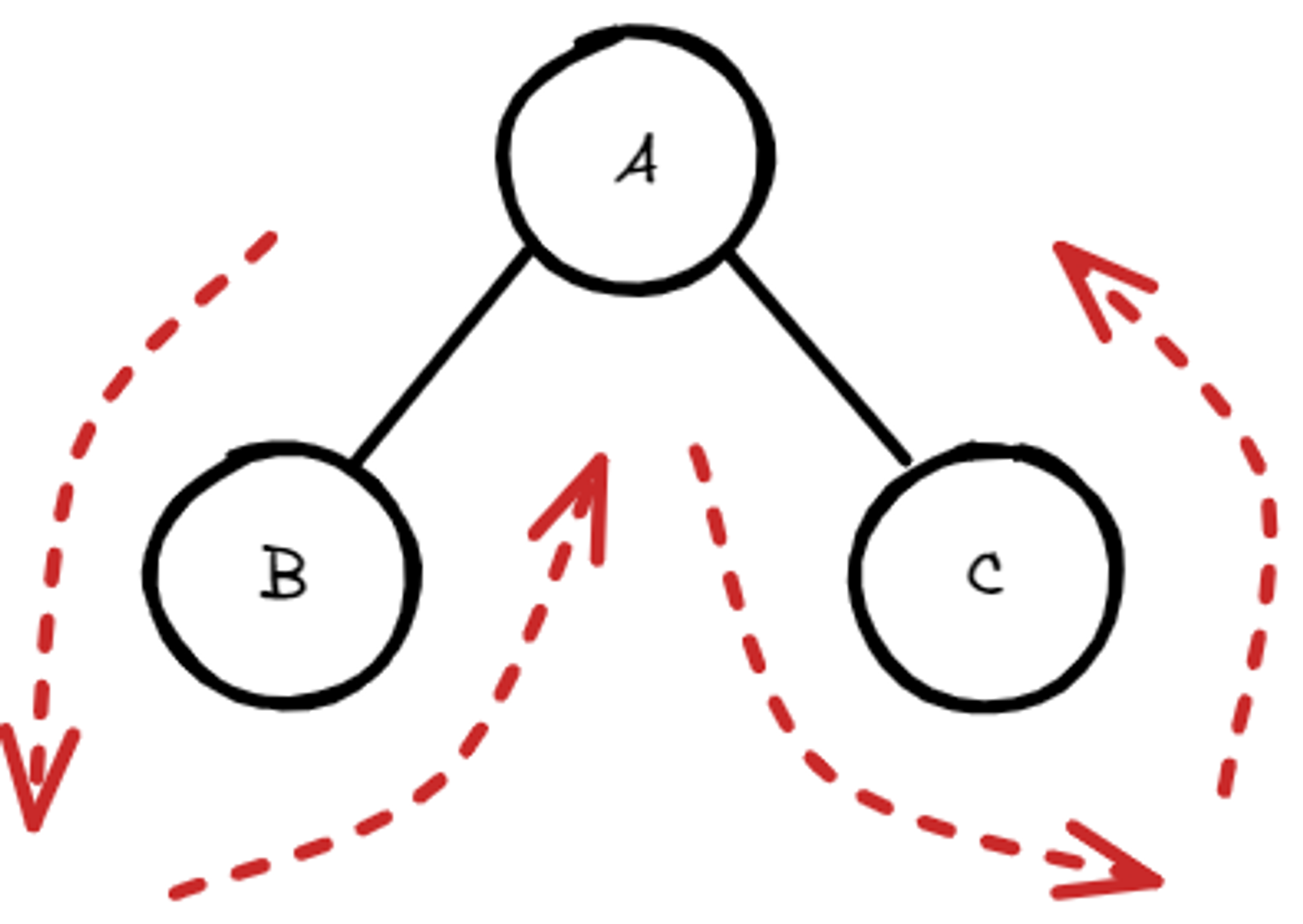
전위 순회: A를 가장 먼저 방문하는 것
- 출력 순서: A(root), B(left), C(right)
- 나(A)를 먼저 방문하고 자식 노드들을 방문한다.
-
중위 순회: A를 중간에 방문하는 것
- 출력 순서: B(left), A(root), C(right)
- 왼쪽 노드를 먼저 방문하고, 나(A)를 방문한 후, 오른쪽 노드를 방문한다.
-
후위 순회: A를 가장 마지막에 방문하는 것
- 출력 순서: B(left), C(right), A(root)
- 자식노드들을 다 방문한 후, 나(A)를 방문한다.
예제
아래와 같은 트리가 있을 때, 각각의 순회에서 어떤 식으로 방문하는 알 수 있어야 한다!
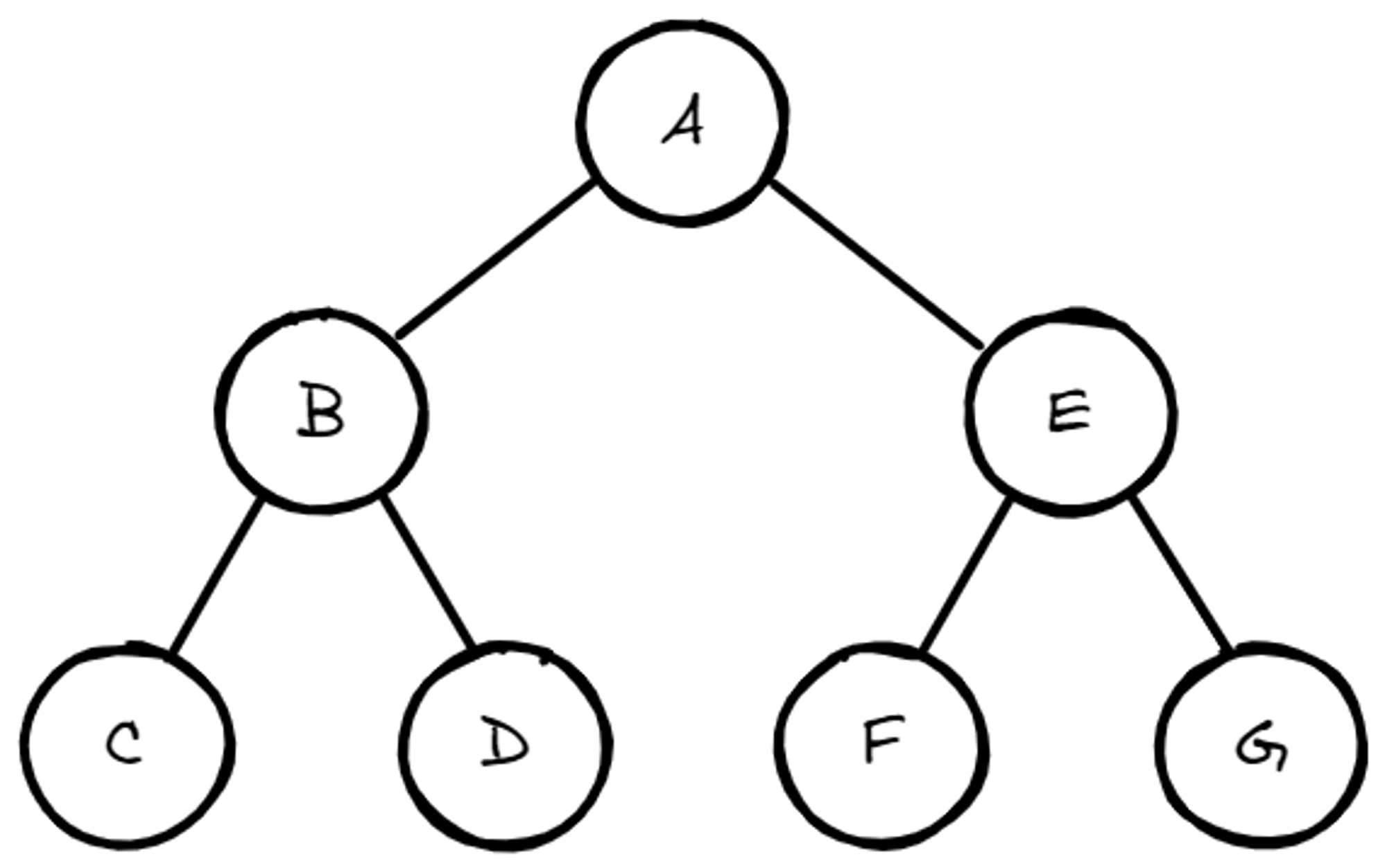
전위 순회: A ⇒ B ⇒ C ⇒ D ⇒ E ⇒ F ⇒ G
중위 순회: C ⇒ B ⇒ D ⇒ A ⇒ F ⇒ E ⇒ G
후위 순회: C ⇒ D ⇒ B ⇒ F ⇒ G ⇒ E ⇒ A
전위, 중위, 후위 순회 시간 복잡도
- 재귀 함수 호출 수: n
- 재귀 함수 하나당 시간 복잡도: O(1)
⇒ 전위, 중위, 후위 순회의 시간 복잡도는 O(n)이다.
리스트(List)와 트리(Tree)의 차이점
리스트는 순서를 매겨 데이터를 나열하는 선형 자료구조였다면, 트리는 비선형적인 자료구조이다.
- 선형 자료구조: 하나의 자료 뒤에 하나의 자료가 존재하는 것
- 비선형 자료구조: 하나의 자료 뒤에 여러개의 자료가 존재하는 것