그래프(Graph)
그래프(G)는 정점(vertex)들의 집합 V와 이들을 연결하는 간선(edge)들의 집합 E로 구성된 자료 구조이다.
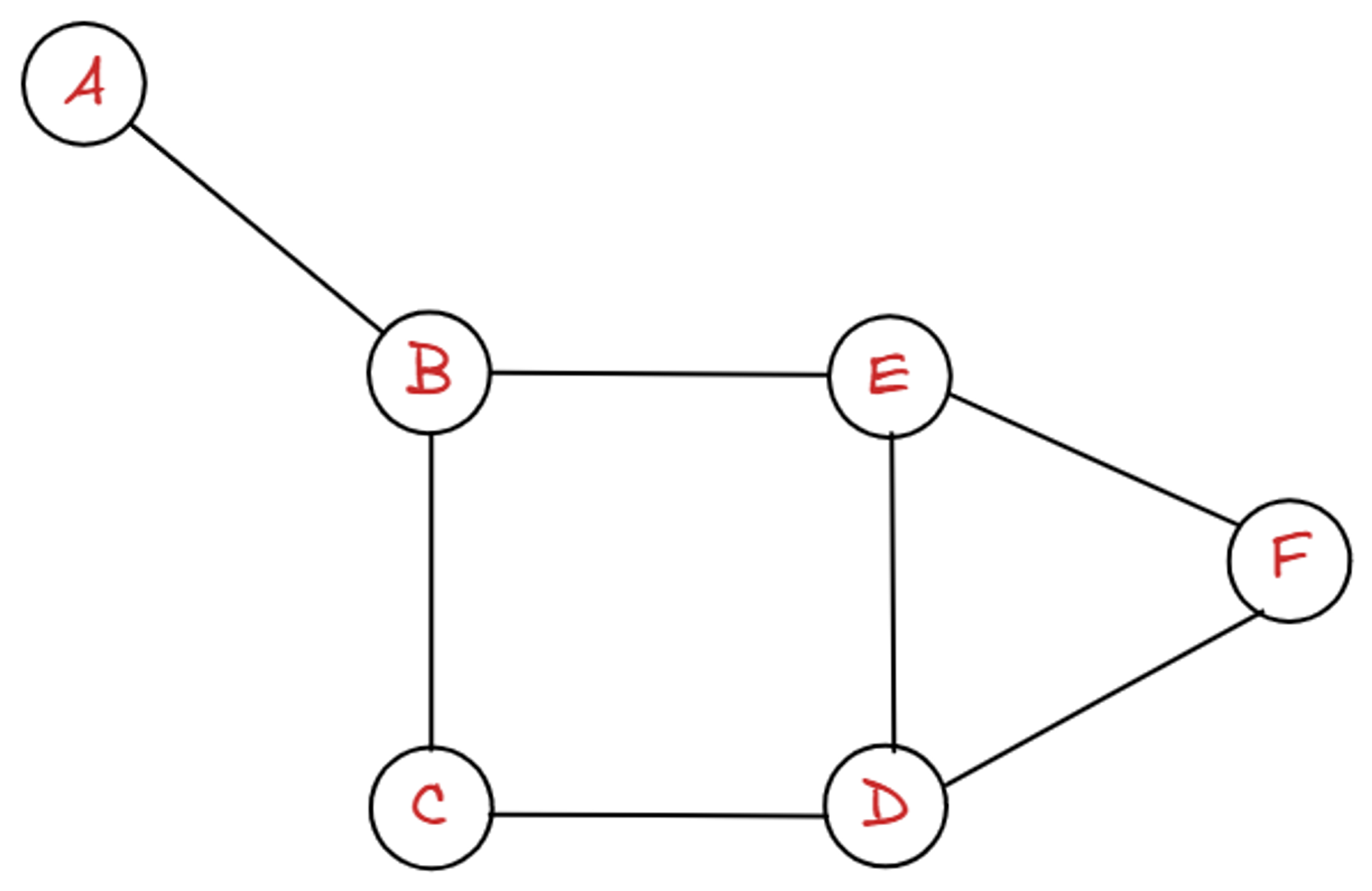
정점들의 집합 V = {A,B,C,D,E,F}, 서로 연결해주는 간선들의 집합 E = {(A,B),(B,C),(B,E),(C,D),(E,D),(E,F),(E,D)}으로 이루어져 있다.
그래프의 활용
그래프는 연결 관계를 표현하기에 현실 세계의 사물이나 추상적인 개념들을 잘 표현 할 수 있다.
- 도시들을 연결하는 도로망: 도시(vertex), 도로망(edge)
- 컴퓨터 네트워크: 각 컴퓨터와 라우터(vertex), 라우터간의 연결 관계(edge)
- 소셜 네트워크 분석: 페이스북의 계정(vertex), follow 관계(edge)
그래프의 종류
1. 무향 그래프 vs 방향 그래프
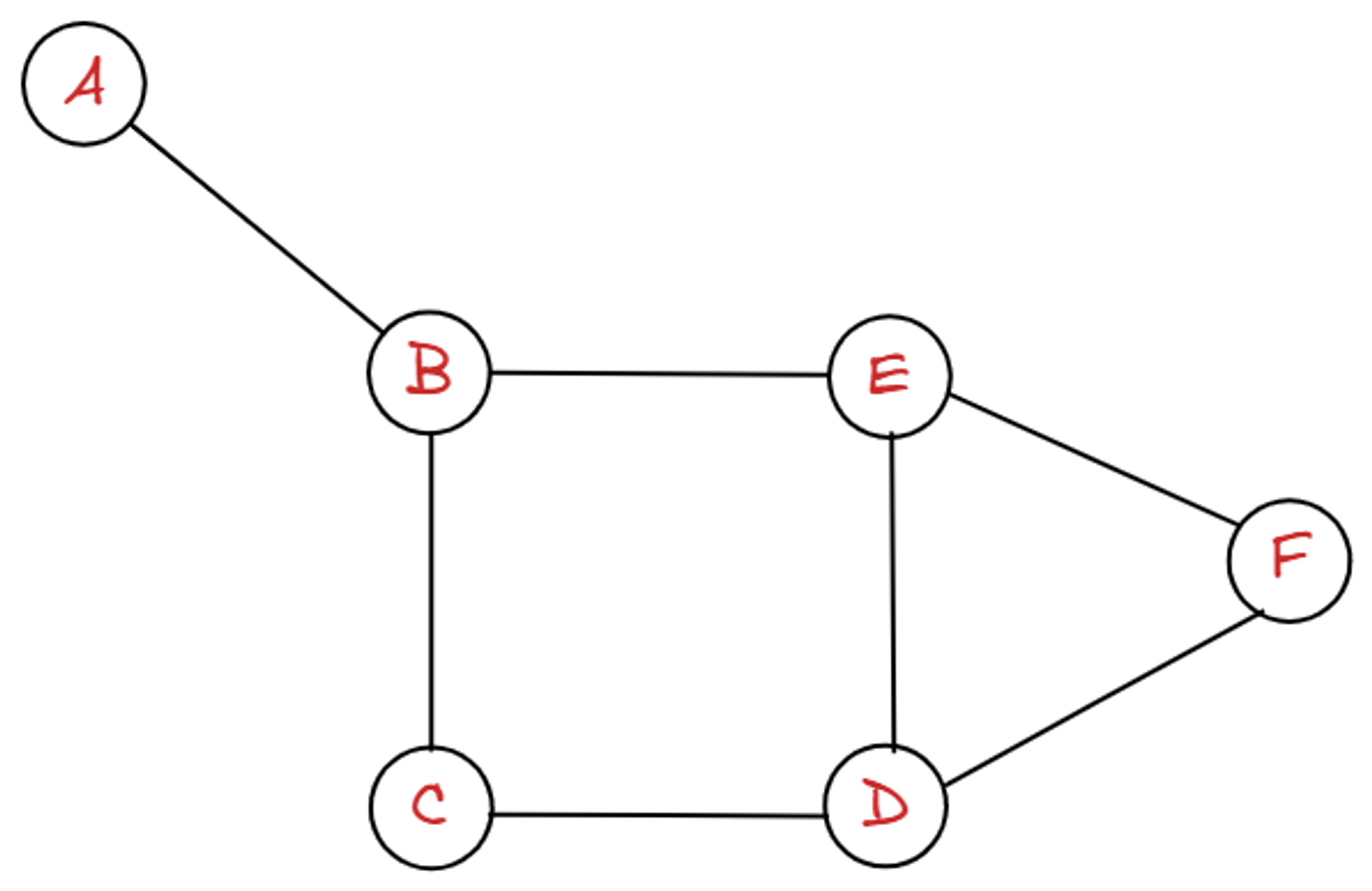
위 그래프는 A ➔ B로 갈 수 있으며, B ➔ A로도 갈 수 있기에 방향이 안 정해져 있는 무향 그래프라고 한다.
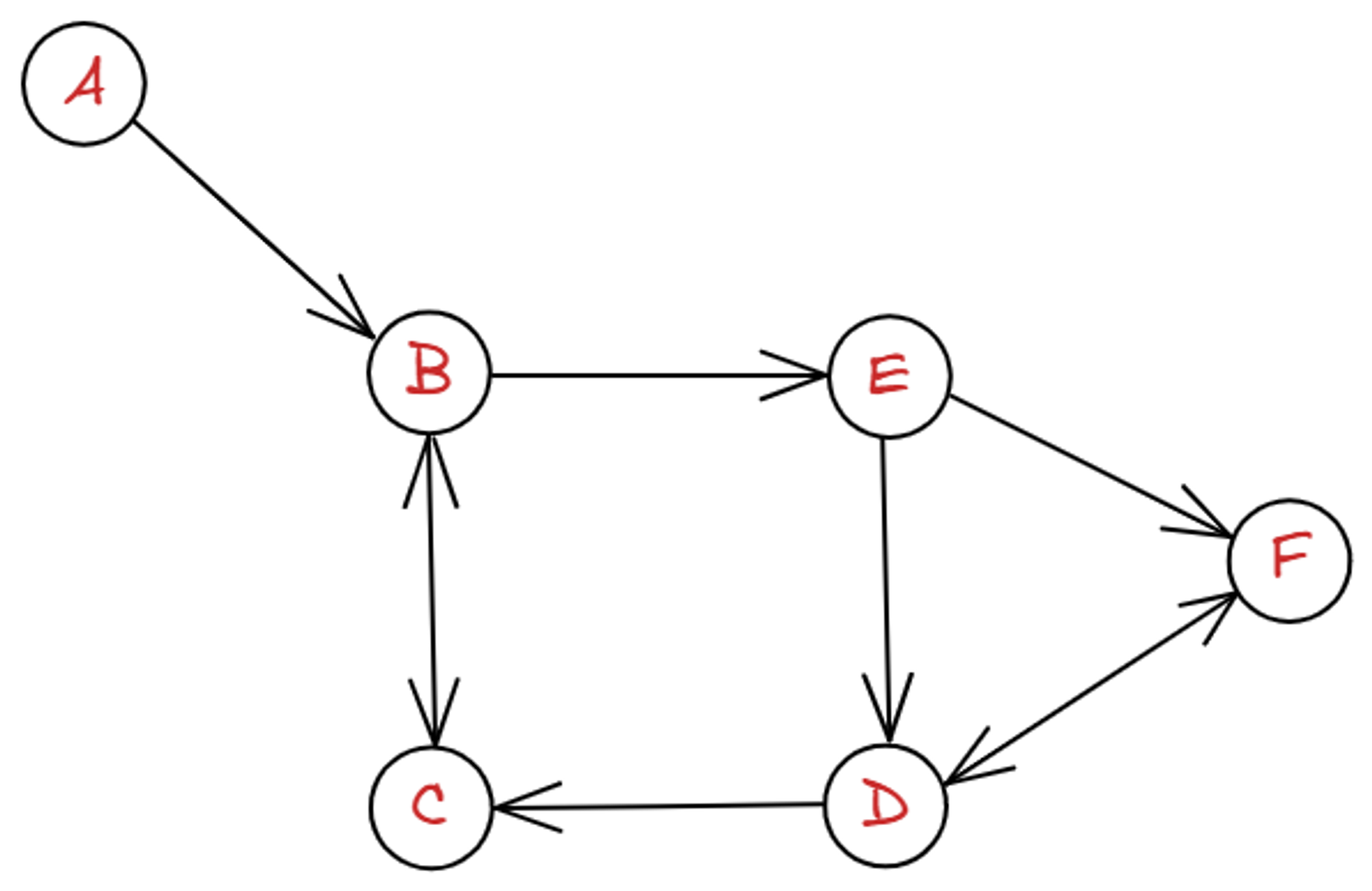
들어오는 간선을 indegree라 하며, 나가는 간선을 outdegree라고 한다. 정점 B를 살펴보면 A와 C로 부터 들어오는 indegree 2개, E로 나가는 outdegree 1개가 있다. 이처럼 방향이 정해져 있는 방향 그래프라고 한다.
💡 코딩테스트에서는 주로 무향 그래프를 다룬다!
2. 다중 그래프 vs 단순 그래프
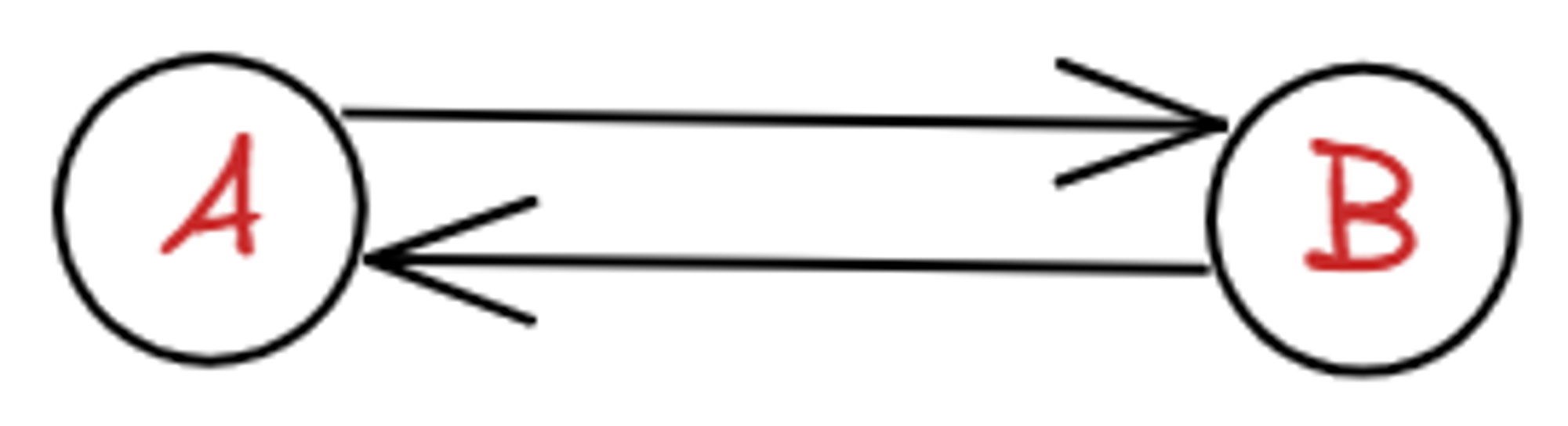
이 두 정점 사이에 indegree가 1개, outdegree가 1개인 그래프를 단순 그래프라고 한다.
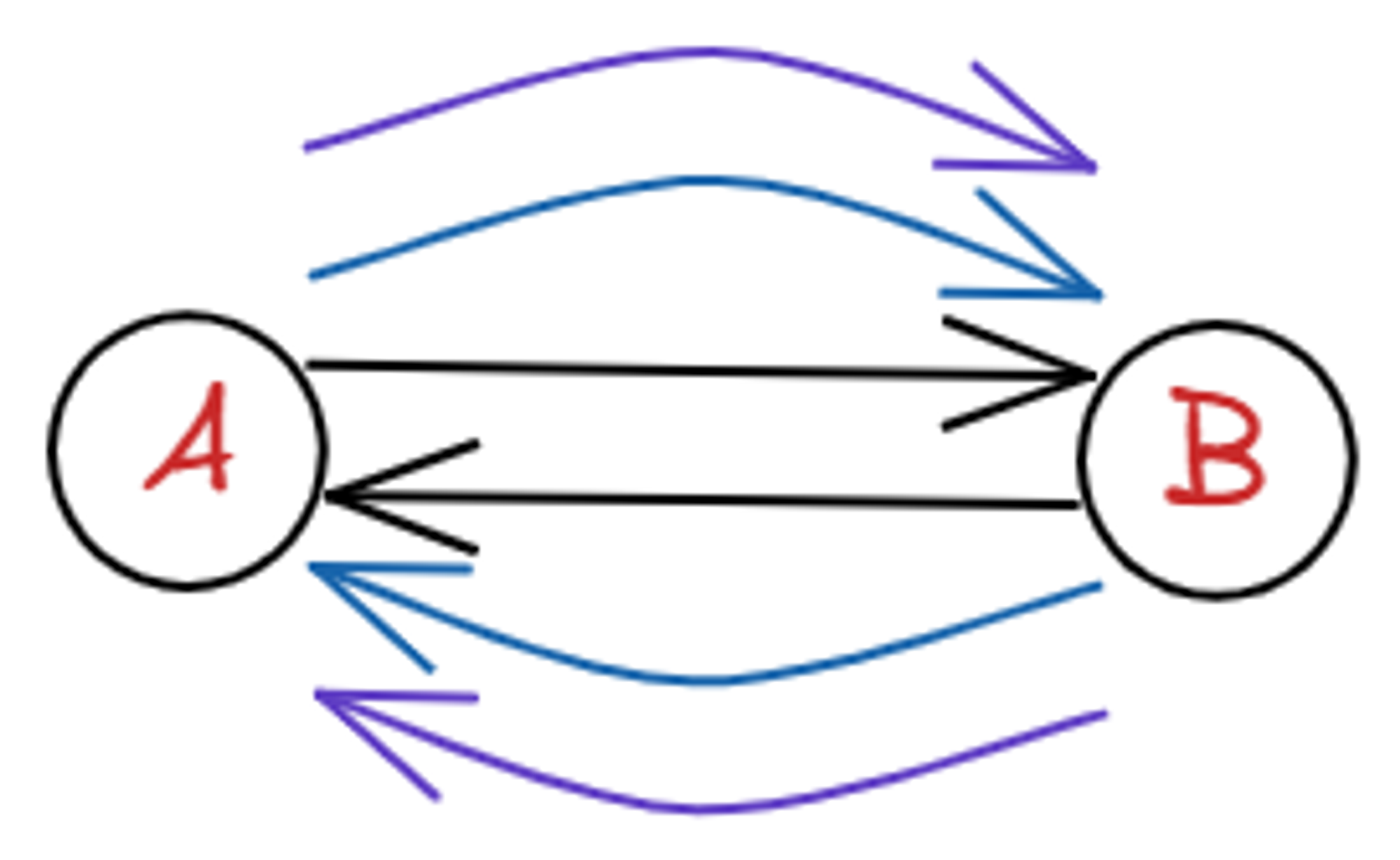
인접해 있는 두 정점 A, B의 관계에서 outdegree와 indegree가 2개 이상인 그래프를 다중 그래프라고 한다.
💡 코딩테스트에서는 주로 단순 그래프를 다룬다!
3. 가중치 그래프
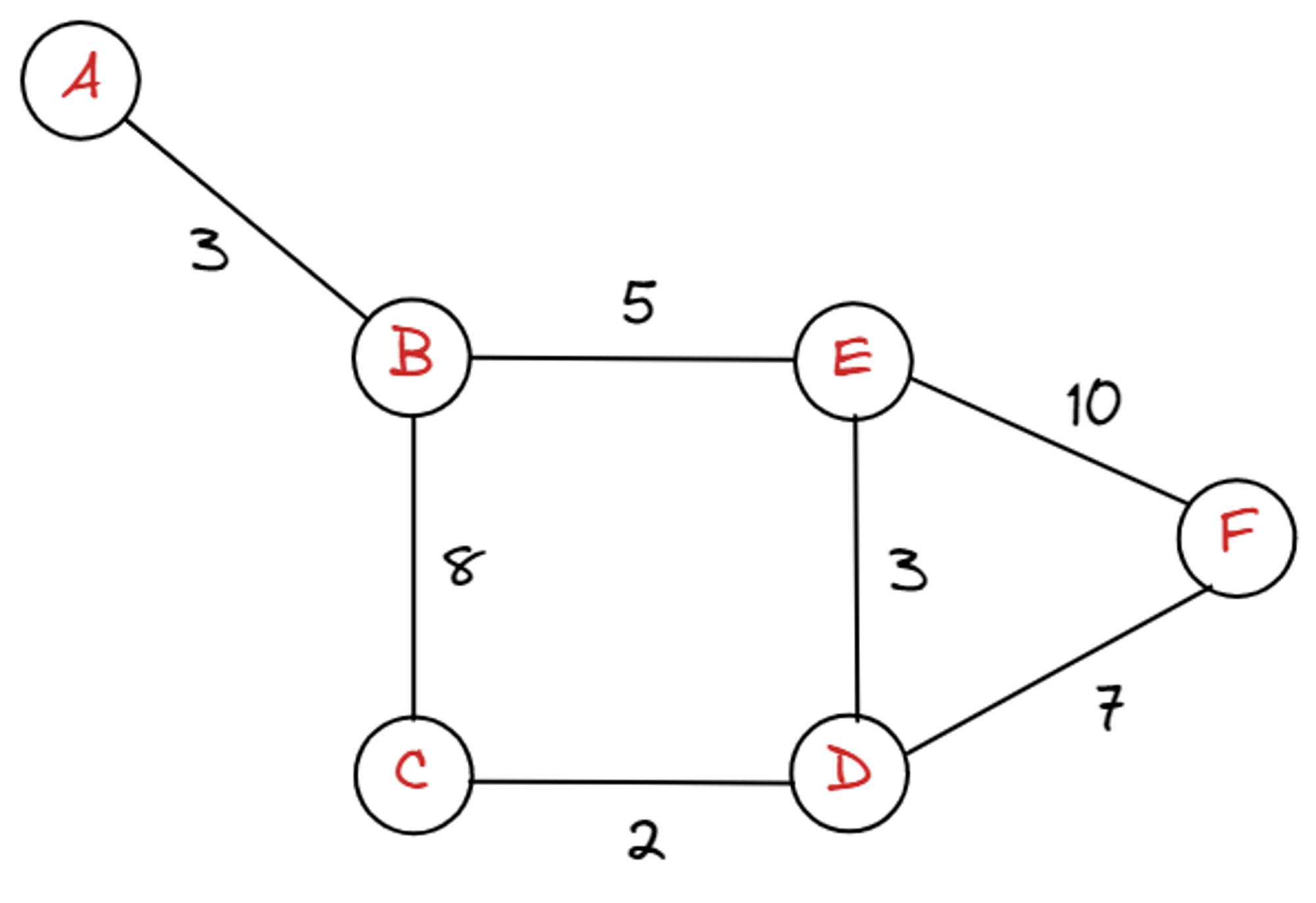
위 사진과 같이 경로마다 가중치(모든 경로의 비용, 시간)가 다른 그래프를 가중치 그래프라고 한다.
💡 가중치 그래프는 추후 다익스트라 알고리즘에서 쓰인다!
그래프의 구현
그래프를 구현 하는 방법 3가지가 있다.
- 인접 행렬
- 인접 리스트
- 암시적 그래프
1. 인접 행렬
행렬은 행(row)와 열(column)에 따라, 정보들을 직사각형 모양으로 배열한 것입니다.
정점끼리 연결 되어 있으면 1, 연결 되어 있지 않으면 0을 대입 한다.
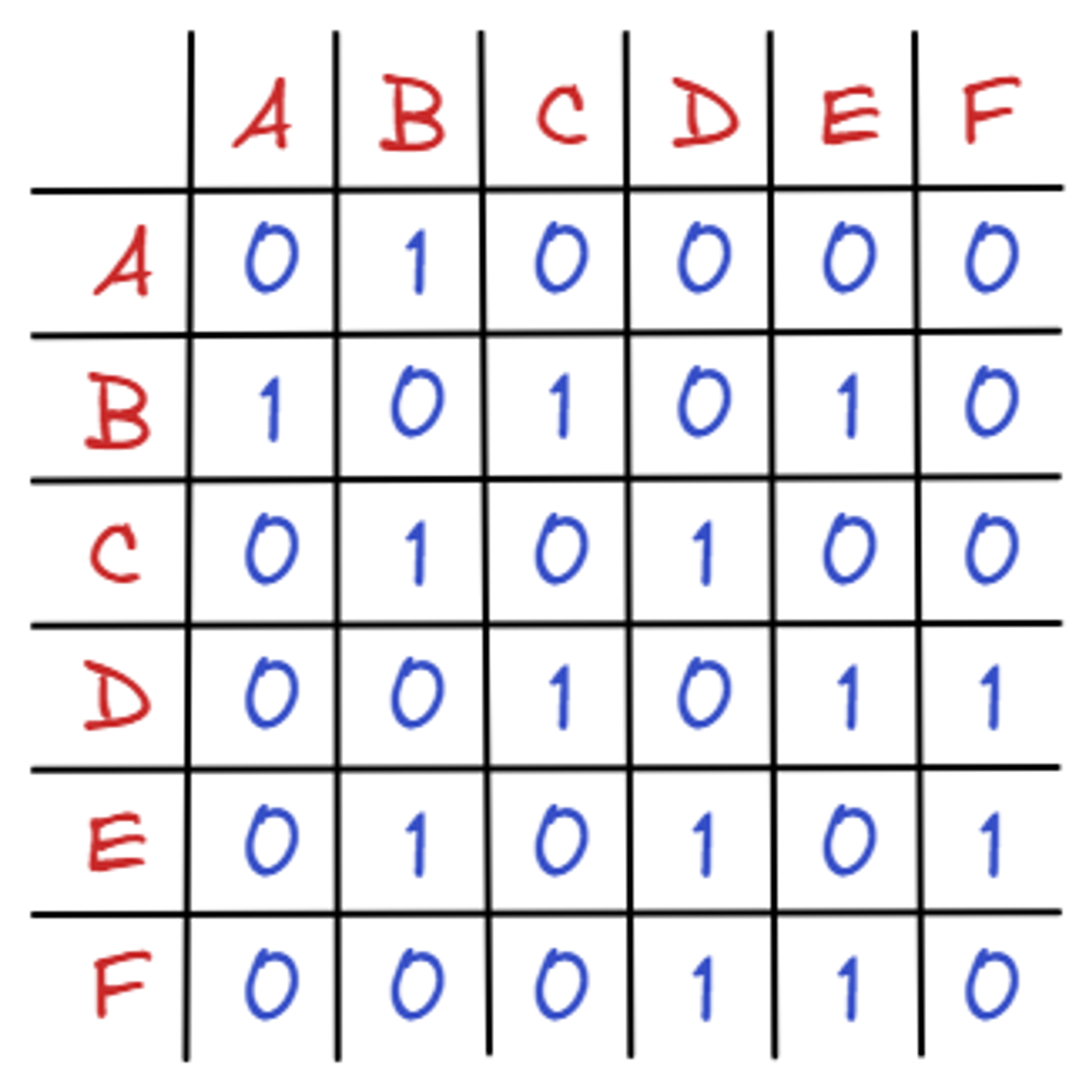
matrix = [
[0, 1, 0, 0, 0, 0],
[1, 0, 1, 0, 1, 0],
[0, 1, 0, 1, 0, 0],
[0, 0, 1, 0, 1, 1],
[0, 1, 0, 1, 0, 1],
[0, 0, 0, 1, 1, 0],
]위 그래프의 특징은 자기 자신(A-A, B-B)을 연결하는 간선이 없기 때문에, 대각선의 값이 모두 0이라는 점과 무향 그래프이기 때문에 대각선을 기준으로 대칭이다.
인정 행렬은 정점은 엄청 많은데, 간선의 개수가 적을 때는 비효율적이다.
2. 인접 리스트
인접 리스트는 딕셔너리 {}의 형태로 정의된다. key에는 정점들이 들어가며, value에는 list형태로 연결 관계를 표시해준다.
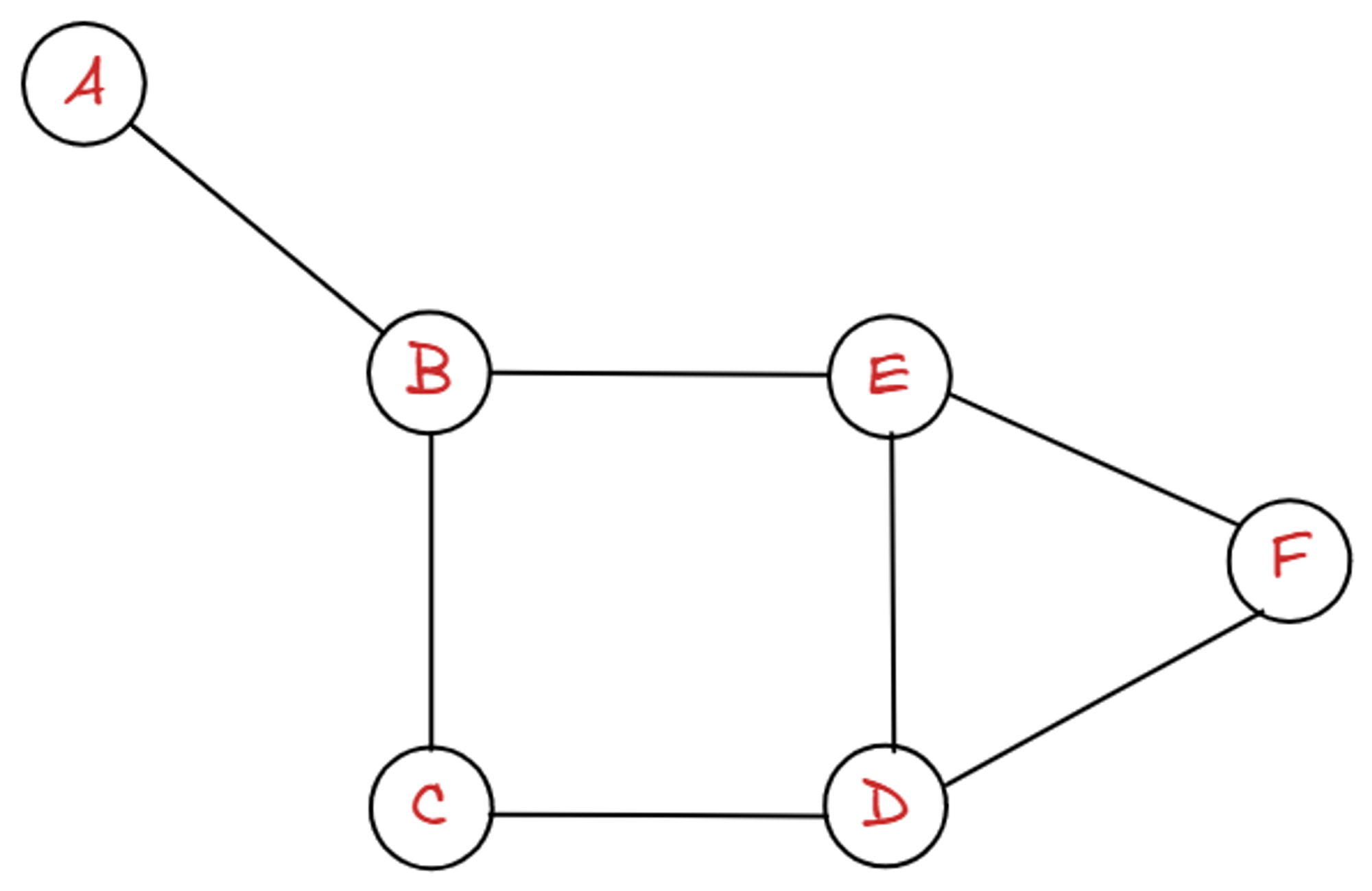
graph = {
"A": ["B"],
"B": ["A", "C", "E"],
"C": ["B", "D"],
"D": ["C", "E", "F"],
"E": ["B", "D", "F"],
"F": ["D", "E"],
}💡 코딩 테스트에서는 주로 인접 행렬보다는 인접 리스트를 사용한다!
3. 암시적 그래프
벽에는 1의 값을, 길에는 0의 값을 넣어주고 각 영역을 좌표의 개념을 도입하여 표현 할 수 있다.

graph = [
[1, 1, 1, 1, 1],
[0, 0, 0, 1, 1],
[1, 1, 0, 1, 1],
[1, 0, 0, 0, 0],
[1, 1, 1, 1, 1],
]⭐️ 그래프의 순회 ⭐️
그래프의 순회는 트리의 순회와 마찬가지로, 모든 정점을 지나야한다. 대표적인 방법으로는 2가지가 있다.
- BFS
- DFS
BFS(Breadth First Search)
트리의 순회인 level order traversal과 매우 유사하다. 그래프를 순회 할 때, 시작점이 주어지는데 이를 루트 노드라 생각하여 level별로 탐색을 하는 것이 BFS이다.
const graph = {
"A": ["B"],
"B": ["A", "C", "E"],
"C": ["B", "D"],
"D": ["C", "E", "F"],
"E": ["B", "D", "F"],
"F": ["D", "E"],
}
let queue = [];
let visited = [];
function bfs(graph, start_v){
visited = [start_v]
queue.unshift(start_v);
while(queue.length){
let cur_v = queue.shift();
for(let v of graph[cur_v]){
if(!visited.includes(v)){
visited.push(v);
queue.push(v);
}
}
}
return visited;
}🔥 BFS 코드는 아주 기본적인 템플릿 코드로써, 머리 속에서 바로 구현이 될 수 있어야 한다!
DFS(Depth First Search)
출발점에서 시작해서, 막 다른 지점에 도착할 때까지 깊게 이동한다. 만약 가다가 막히면 다시 그 전 노드로 돌아가고, 또 길이 있으면 깊게 이동하는 식을 과정을 통해 그래프를 순회한다.
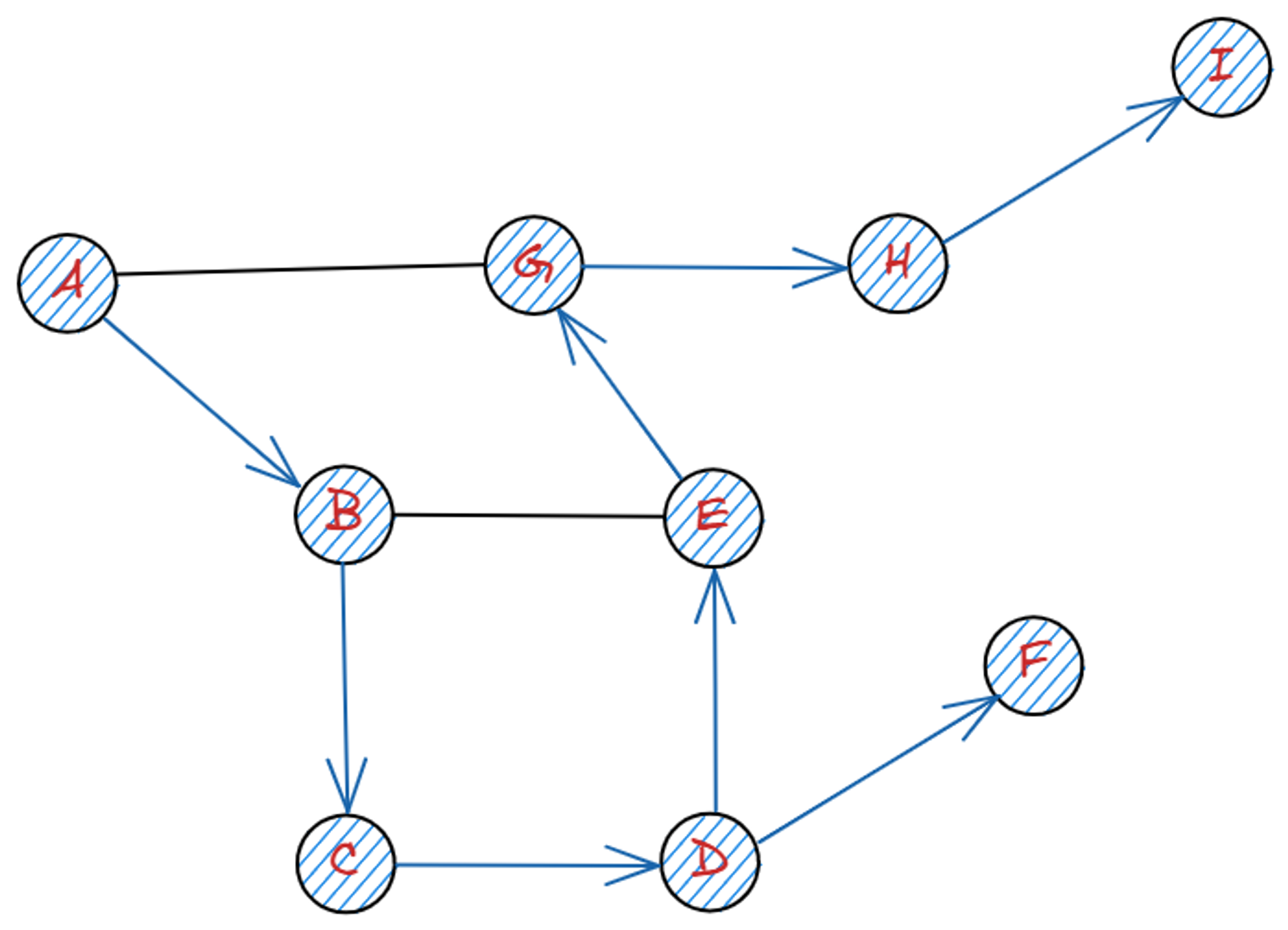
1. A ➔ B ➔ D ➔ E(알파벳 순) ➔ G ➔ H ➔ I
2. I ➔ H ➔ G ➔ E ➔ D(되돌아가기)
3. D ➔ F
4. F ➔ D ➔ C ➔ B ➔ A(되돌아가기)
DFS는 스택과 재귀로 구현할 수 있다!
const graph = {
"A": ["B", "D", "E"],
"B": ["A", "C", "D"],
"C": ["B"],
"D": ["A", "B"],
"E": ["A"]
}
let visited = [];
function dfs(cur_v){
visited.push(cur_v);
for(let v of graph[cur_v]){
if(!visited.includes(v)){
dfs(v);
}
}
}BFS와 DFS 시간 복잡도
각각의 순회는 모든 정점(V)들을 탐색해야 하고 그러기 위해서는 정점에 연결된 edge(E)들을 모두 확인해봐야 한다. 따라서 시간 복잡도는 O(V + E)입니다.
