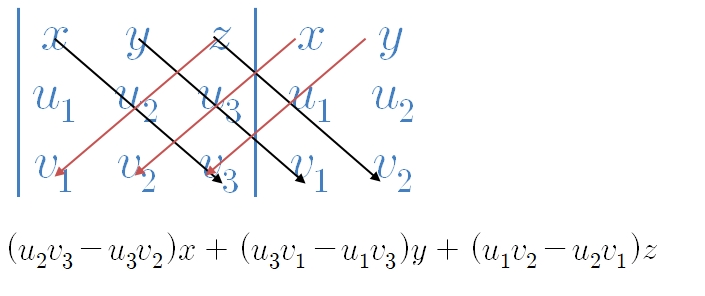외적 (Cross Product)

📄 외적 (Cross Product)

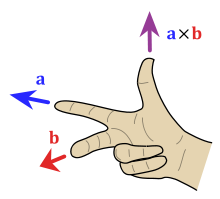
• 두 벡터에 대하여 모두 수직인 벡터를 반환하므로, 3차원 벡터에서만 성립
• 교환법칙이 성립하지 않음
  

✏️ 구현하기

• A×B = [(AyBz - AzBy), (AzBx - AxBz), (AxBy - AyBx)]
  

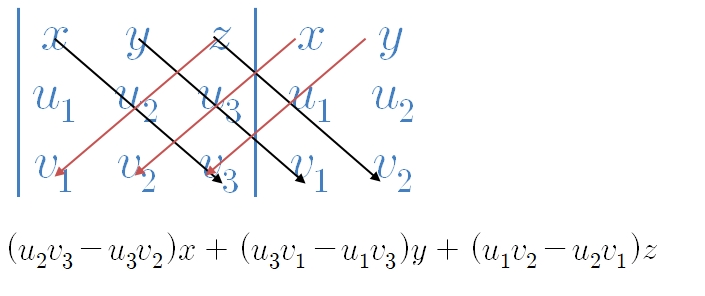
Vector3 vector_cross(Vector3 a, Vector3 b)  
{  
    return new Vector3(  
        a.y * b.z - a.z * b.y,  
        a.z * b.x - a.x * b.z,  
        a.x * b.y - a.y * b.x);  
}

✏️ 평행사변형의 넓이

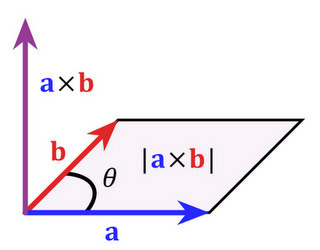
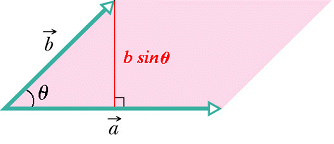
• 외적의 크기는 두 벡터로 이루어진 평행사변형의 넓이다.
• |A×B| = |A||B|sinθ
  

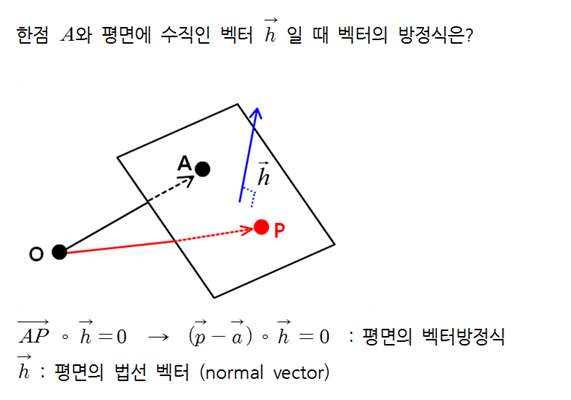
✏️ 평면의 법선 벡터

• 세 개의 정점으로 구성되는 삼각형의 두 변을 이루는 벡터의 외적을 구하여 정규화(Normalize)해주면 삼각형이 존재하는 평면의 법선 벡터가 나온다.
  

✏️ 좌우 판별

• 자신의 Forward vector와 타겟을 바라보는 Direction vector의 외적을 구한다.
• 외적 결과를 Up vector와 내적한다.
• 결과가 양수면 오른쪽, 음수면 왼쪽, 0이면 평행.

Vector3 targetDir = this.target.position - this.transform.position; // 타겟 방향으로 향하는 벡터
Vector3 crossVec = Vector3.Cross(this.transform.forward, targetDir); // 포워드와 외적
float dot = Vector3.Dot(crossVec, Vector3.up);

if (dot > 0) // 양수면 오른쪽
{
     desc = "오른쪽";
}
else if (dot < 0) // 음수면 왼쪽
{
     desc = "왼쪽";
}
else // 0이면 평행
{
     desc = "평행";
}

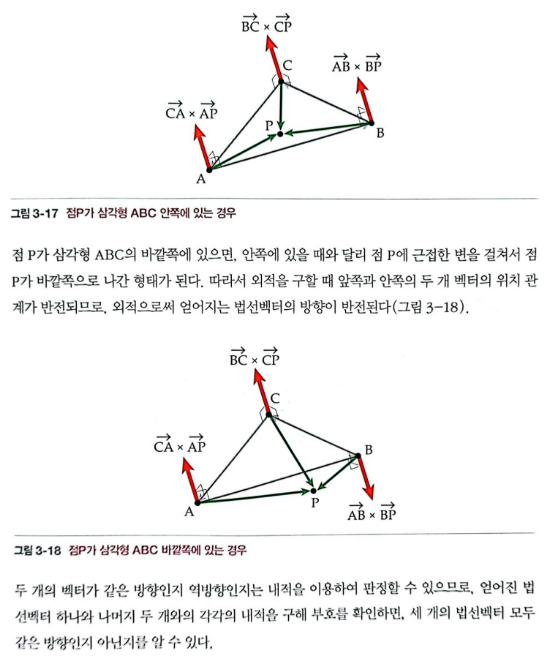
✏️ 교차 판별

• 모든 외적의 방향을 비교하여 교차(Intersect), 충돌(Collision) 여부를 판정할 수 있다.
  

---

자료 출처

• https://lee-seokhyun.gitbook.io/game-programming/client/easy-mathematics/3d/