경사 하강법(Gradient Descent, GD)

경사 하강법은 손실 함수의 경사(Gradient)가 작아지는 방향으로 업데이트 하는 방법이다. 매 Iteration마다 해당 가중치에서 비용 함수의 도함수(=비용 함수를 미분한 함수)를 계산해 경사가 작아질 수 있도록 가중치를 변경해준다.

기울기의 반대로 이동하는 이유는 기울기가 양수일 때 기울기를 줄이려면 음수 방향으로 움직여야 하고, 기울기가 음수일 때는 기울기를 줄이려면 양수 방향으로 움직여야 하기 때문에 기울기의 반대로 이동하는 것이다.

옵티마이저 (Optimizer)

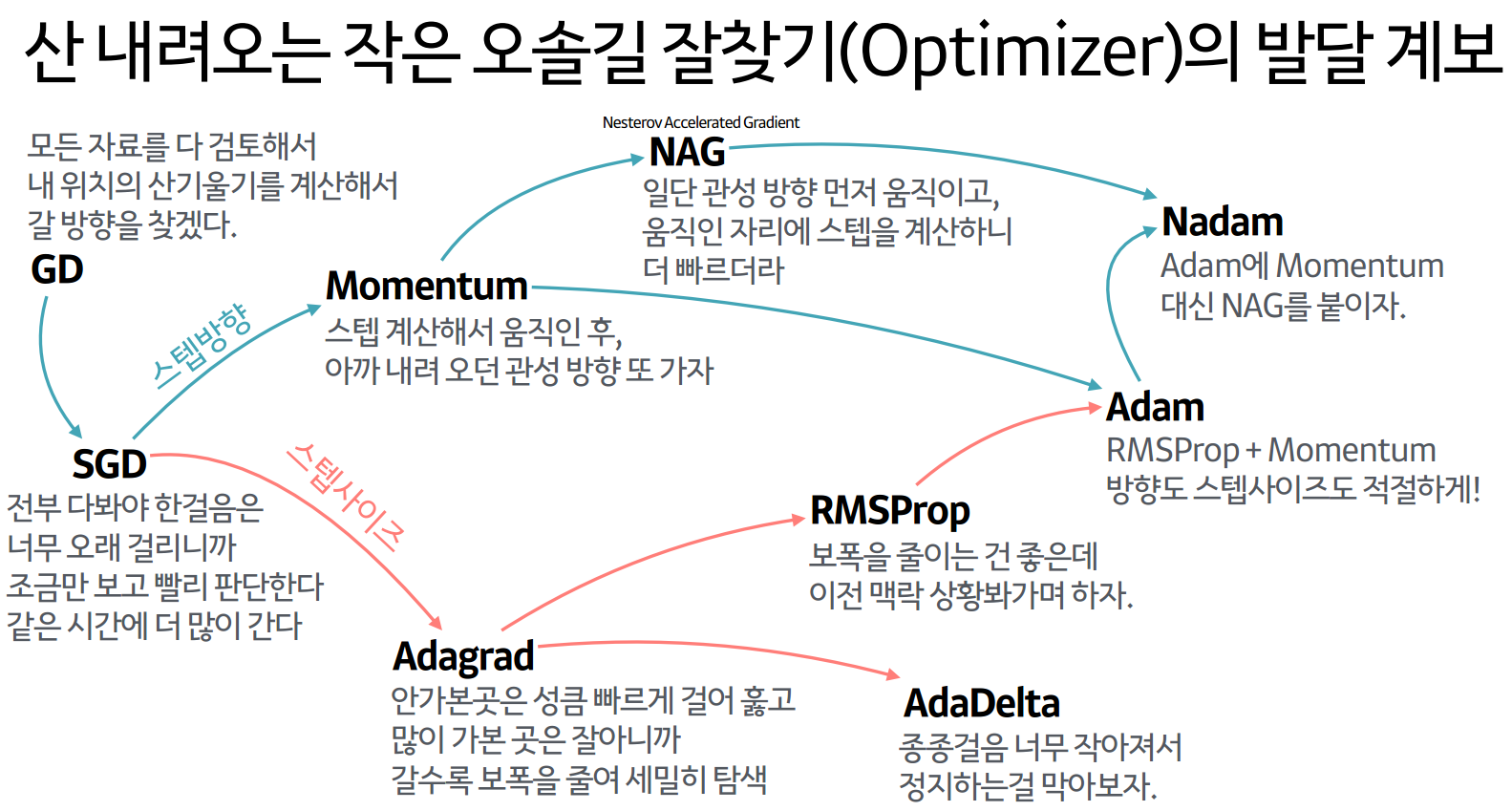
옵티마이저는 손실을 최소화 시키면서 경사를 내려가는 방법을 결정하는 알고리즘이다. 최적의 Gradient Descent를 적용하며 최소의 loss로 빠르고 안정적인 방법을 찾는 것이다.
옵티마이저에 대해서 쉽게 말하자면 산의 정상에 오르고 나서 하산하려고 할 때, 어떻게 산을 내려갈지를 결정하는 것이 바로 옵티마이저라고 할 수 있다.

SGD (Stochastic Gradient Descent)

SGD는 한 번에 전체 학습 데이터에서 하나씩 랜덤으로 값을 뽑아서 학습을 시킨 뒤 계산된 손실 정보를 역전파해 신경망의 가중치를 업데이트 한다.

SGD는 한번의 Iteration마다 1개의 데이터를 사용하기 때문에 가중치를 빠르게 업데이트 할 수 있다는 장점을 갖고 있다. 하지만 1개의 데이터를 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다는 단점도 가지고 있다.

Mini-batch

Mini-batch 경사 하강법은 SGD와 GD가 적절히 융화된 경사 하강법이다. SGD와 다르게 N개(=배치 사이즈)의 데이터로 미니 배치를 구성해 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치를 업데이트 해준다.

일반적으로 배치 사이즈는 2의 배수로 설정한다.

#of Data = Batch_size X Iteration

또한 데이터셋을 이루는 데이터의 수(#of Data), 배치 사이즈, Iteration이 위와 같은 식을 만족한다.

Momentum

Momentum은 기존의 SGD에서 velocity term이 추가된 버전인데, velocity term은 속도를 조절하는 역할을 맡아 관성 효과를 낸다.
관성의 특성을 갖고 있기 때문에 기울기 변화가 심한 방향으로는 값을 더 많이 개선하고, 기울기 변화가 완만한 방향으로는 값을 덜 계산하는 특징이 있다.

AdaGrad (Adaptive Gradient)

Adagrad는 파라미터마다 다른 학습률을 적용시키도록 고안됐다. 자주 등장하는 파라미터는 낮은 학습률을, 가끔 등장하는 파라미터에는 높은 학습률을 적용해준다.
이렇게 다른 학습률을 적용시킴으로써 변동을 줄이는 효과가 있다.

Adagrad는 알아서 적절한 학습률을 적용시켜준다는 장점이 있지만, 많은 반복 학습 후에는 파라미터가 거의 갱신되지 않는다는 단점이 있다.

RMSProp

RMSProp는 Adagrad 와 크게 다르지 않다. Adagrad의 문제점을 개선하기 위해서 계산식에 지수이동평균을 적용한 것이 바로 RMSProp이다.
RMSProp의 핵심은 보폭을 갈수록 줄이되, 이전 기울기 변화의 맥락을 살피자는 것이다.

Adam

Adam은 가장 흔하게 이용되는 옵티마이저로 Momentum에 적용된 그래디언트 조정법과 Adagrad에 적용된 학습률 조정법의 장점을 융합한 옵티마이저이다.