[TIL] Recall과 Precision, ROC curve

hyewon·2021년 10월 27일

TIL

목록 보기

22/59

3줄 요약

Recall : 실제 Positive 중 올바르게 Positive라고 예측된 비율
Precision: Positive라고 예측된 것 중 실제 Positive를 맞춘 비율
Roc curve: 다양한 임계점에 대한 TPR과 FPR의 성능을 표시해주는것

Recall과 Precision

Confusion Matrix

Recall과 Precision에 대해서 정의하기 전에 먼저 알고 있으면 Recall과 Precision를 이해하기가 좀 더 쉬울수 있도록 도와주는 것이 바로 Confusion Matrix라고 생각한다.

Confusion Matirx는 다음과 같이 생긴 Matrix를 Confusion Matrix라고 부른다.

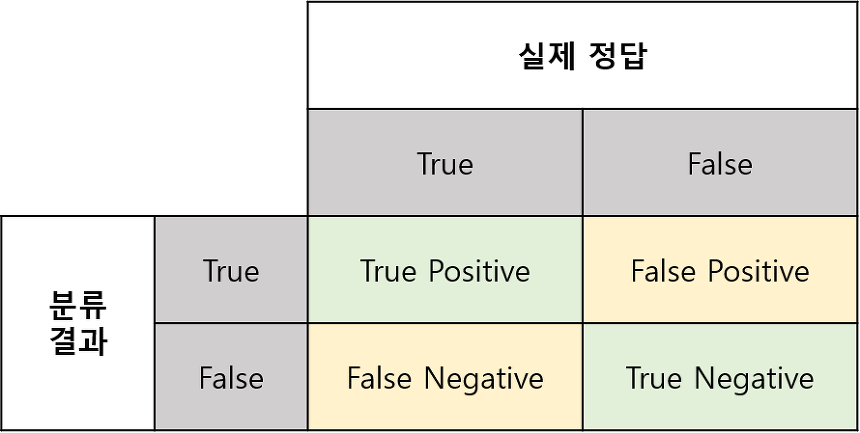
Confusion Matrix를 봤을때 굉장히 익숙했었는데 바로 예전에 공부했었던 Type of Error의 표와 똑같았다.

위의 표를 풀어서 설명하자면 이렇다.

True Positive(**TP**): 실제 Positive 값을 Positive로 잘 예측했다.
False Positive(**FP**): 실제 False 값을 Positive로 잘못 예측했다.
False Negative(**FN**): 실제 Positive 값을 Negative로 잘못 예측했다.
True Negative(**TN**): 실제 Negative 값을 Negative로 잘 예측했다.

실제로는 주로 괄호 안의 약자들이 많이 쓰이기 때문에 괄호 안의 약자에 익숙해지는 것이 좋다.

Recall (재현율)

Recall은 실제 Positive 값 중에서 모델이 Positive라고 예측한 값의 비율이다.

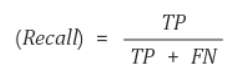
Precision (정밀도)

Precision은 모델이 Positive라고 예측한 값 중에서 실제 Positive한 값의 비율이다.

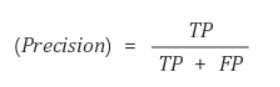
Recall - Precision trade off

trade-off는 두마리의 토끼를 모두 다 잡을 수 없다고 생각하면 이해하기가 쉽다. Recall과 Precision 사이에 trade off 관계 있다는 것은 Recall이 높아지게 되면 Precision의 값은 낮아질 수밖에 없고 반대로 Precision이 높아지게 되면 Recall이 낮아질 수밖에 없다는 것이다. 이러한 관계에는 Bias와 Bariance를 떠올리게 한다.

예를 들기 위해서 구글에서 사진을 한 장 갖고 왔습니다.

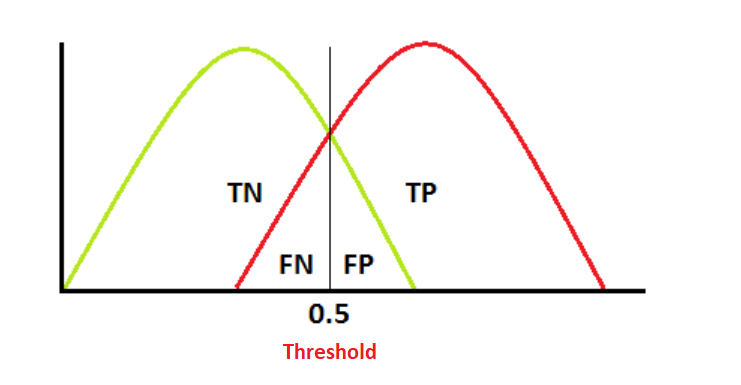
Threshold(default value = 0.5)를 기준으로 보면 편하다. Threshold가 왼쪽으로 움직이면 (threshold < 0.5), 모델이 Positive라고 예측하게 되는 값이 많아지므로 FN의 값이 낮아지게 된다.
반대로 Threshold가 오른쪽으로 움직이게 되면(threshold > 0.5), 모델이 Negative라고 예측하게 되는 값이 많아지므로 FP의 값이 낮아지게 된다.

이게 Recall과 Precision의 trade off에 무슨 상관이냐고 하면 Recall과 Precision의 공식을 보면 각각 분모에 FN과 FP가 들어가기때문이라고 설명할 수 있다.

따라서 Threshold를 낮추면 Recall은 커지지만 Precision은 낮아지게 되고, Threshold를 높이면 Recall은 낮아지지만 Precision은 높아지게 된다.

Recall과 Precision의 구체적인 예

Recall과 Precision을 실생활에서 일어날법한 일들로 예를 들어보고자 한다. QnA 시간에 이걸 진행했는데 나는 말이 너무 헷갈려서 이게 Recall이라고? 이게 왜 Recall인가요 하면서 설명을 부탁했었다 ... 때문에 제 설명에 틀린 부분이 있다면 지적 부탁드립니다 아직도 조금 헷갈리거든요😉