사실 Ridge Regression은 오늘 배운 건 아니고..수요일에 배웠는데 그 날 정리하는걸 까먹어서 시간이 남는 오늘에서야 작성합니다..😅😅

Ridge Regression (릿지 회귀)

Ridge Regression(릿지 회귀)은 다중 회귀 모델에서 람다로 가중치를 줌으로써 편향 에러를 조금 더 더하는 대신 모델의 분산 에러를 줄이는 방법으로 일반화를 유도하는 모델이다.

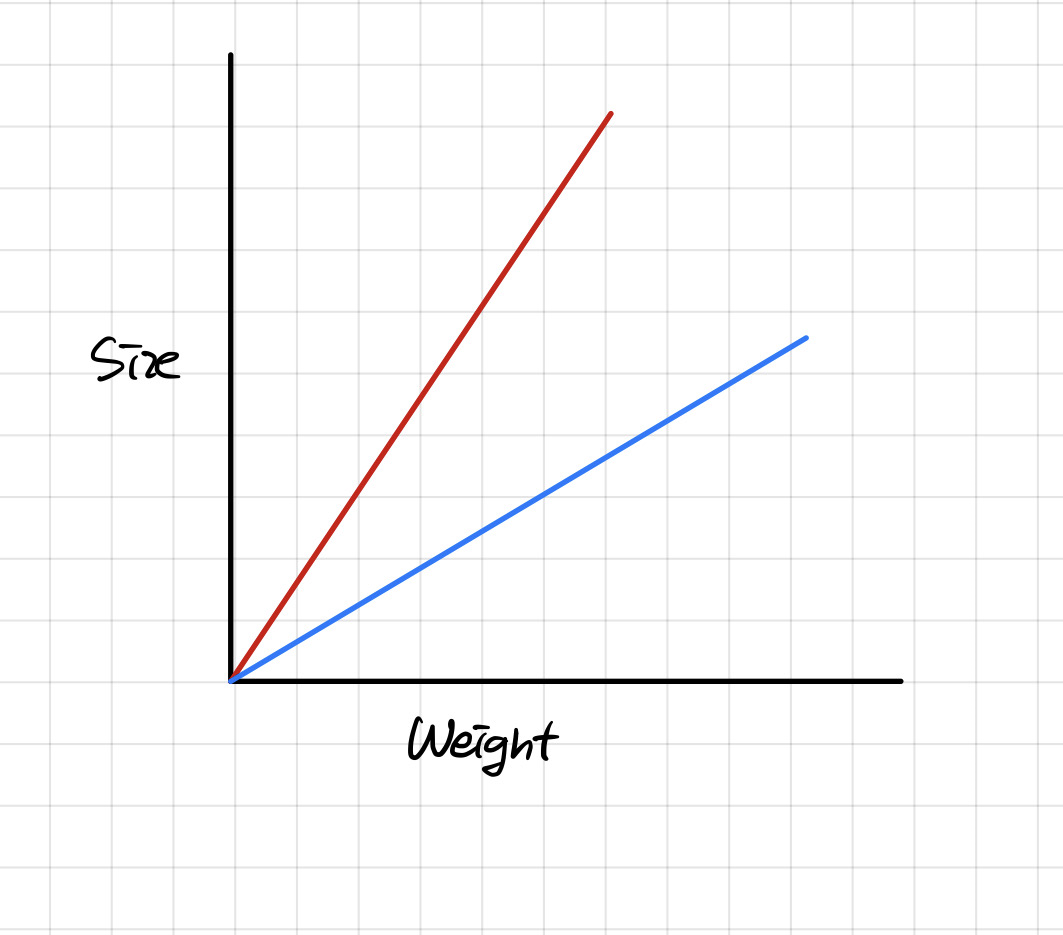
위의 그림에서 빨간선이 다중 회귀 모델이라면 릿지 회귀는 빨간선에 가중치를 줌으로써 빨간선에서 파란선으로 바뀌게끔 만들어준다.

One-Hot Encoding

sklearn은 아쉽게도 범주형 변수를 입력값으로 처리해주지 않는다. 때문에 범주형 변수를 One-Hot Encoding을 통해서 바꿔줘야 한다.

원-핫 인코딩은 범주형 변수를 True(1)와 False(0)로 바꿔주는 기법이다. 원-핫 인코딩을 수행하면 각 카테고리에 해당하는 변수들이 모두 차원에 더해지게 되므로 카테고리의 변수가 많은 경우는 사용하기에 부적합하다. 그리고 카테고리의 범주를 1, 2, 3 .. 이러게 순서형 인코딩을 하게 되면 범주형 값들이 대소관계를 지니게 되므로 주의해야한다.

from category_encoders import OneHotEncoder

df = pd.DataFrame({'City': ['부산', '서울', '대구', '인천', '대구', '부산', '서울']})

encoder = OneHotEncoder(use_cat_names = True)
encoder_df = encoder.fit_transform(df)

# pd.get_dummies를 사용할 경우

dummies_df = pd.get_dummies(df, prefix = ['City'])

# sklearn.preprocessing.OneHotEncoder도 있지만 
# 이 모듈보다 category_encoders의 OneHotEncoder 모듈이 
# 사용하기 더 편리해서 category_encoders의 모듈을 사용하면 된다.

위의 코드를 실행시키면 다음과 같은 결과를 얻을 수 있다.

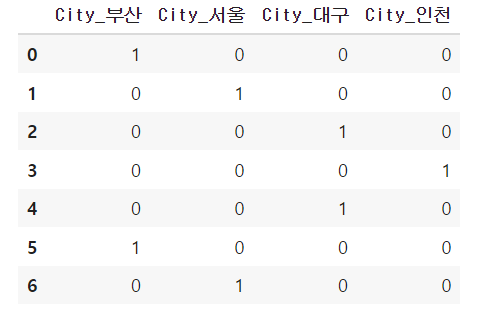
또한 지금의 예제에서는 첫 행을 삭제하지 않고 모든 행을 그냥 출력시켰지만, 원래는 첫 행을 다중공산성 문제때문에 삭제해주고 사용을 하므로 참고해야한다.

+) 다중 공산성이란? 독립 변수들간의 강한 상관 관계가 나타나서 독립 변수들이 독립적이지 않게 되는 문제가 발생하게 되는 현상

+) 코랩에서 from category_encoders import OneHotEncoder를 사용해서 원-핫 인코딩을 할 경우 해당 모듈을 찾을 수 없다는 에러가 뜨는데

pip install --upgrade category_encoders

위의 코드를 실행시켜서 category_encoders를 업그레이드 해주면 에러 없이 작동된다.

특성 선택(Feature Selection)

특성 선택은 특성 공학(Feature Engineering)으로 과제에 적합한 특성을 만들어 내는 과정이다. 그러니까 데이터의 종류가 많은 경우에 중요하다고 생각되는 특징 데이터만 선택해서 특징 데이터의 종류를 줄여주는 방법이다.

좋은 특성을 뽑기 위해서는 특성끼리는 상관성이 적으면서도 타켓 특성과는 상관성이 큰 특성을 뽑아야한다.

이러한 특성 선택을 위해서 사이킷런에서 제공하는 SelectKBest를 사용해서 중요한 특성을 선택할 수 있다.

from sklearn.feature_selection import chi2, SelectKBest

X, y = load_iris(return_X_y=True)
X.shape # (150, 4)

# target 데이터와 가장 관계된 특성 2개를 고른 뒤 학습 데이터에 fit_transform을 시켜줌
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
X_new.shape # (150, 2)

릿지 회귀(Ridge Regression) 모델 만들기

릿지 회귀는 위에서 설명했다시피 선형회귀모델에 가중치를 이용해 다중회귀선을 훈련 데이터에 덜 적합되도록 만든 모델이다. 릿지 회귀는 L2 Regression이라고도 불린다.

아래는 Ridge Regression의 식이다. 참고로 $\lambda$는 alpha, lambda, regularization parameter, penalty term 모두 같은 뜻으로 사용하며 코드에서는 주로 alpha란 단어로 사용하고 있는 것 같다. 추가적으로 $\lambda$의 값이 커질 수록 직선의 기울기가 0에 가까워진다.

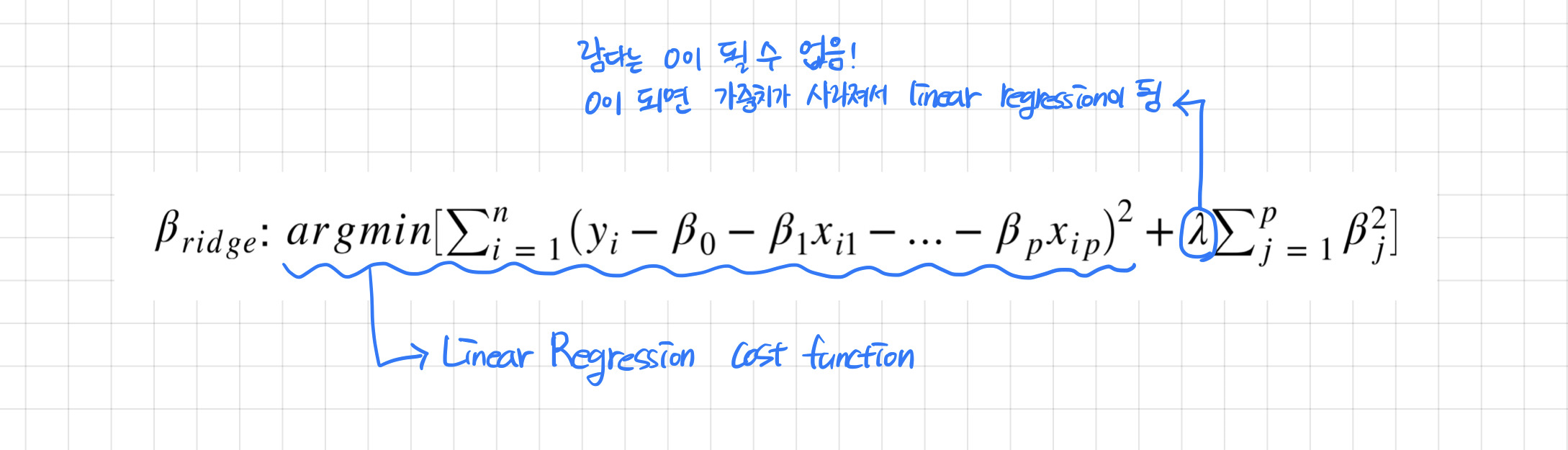
sklearn에서는 내장된 교차검증 알고리즘을 적용하는 RidgeCV 모듈을 제공한다. 물론 RidgeCV가 아닌 Ridge 모듈도 제공해주고 있다.

from sklearn.linear_model import RidgeCV

alphas = [0.001, 0.01, 0.1, 0, 1]

# alphas = 시도할 $\lambda$의 값의 배열. 넣은 값 중 최적의 값을 찾아서 해당 값으로 모델을 학습시킴. 
# cv (cross validation) = 교차 검증 분할 전략 결정
ridge = RidgeCV(alphas = alphas, cv = 3).fit(X_train_data, y_train_data)