Logistic Regression
Logistic regression은 이름은 회귀이지만 분류 문제를 푸는 지도 학습 알고리즘 모델이다. 샘플이 특정한 범주에 속할 확률을 추정하는데 사용한다.
회귀 vs 분류
우선 회귀 문제는 예측하고자 하는 변수와의 관계를 볼 때 많이 사용한다. 회귀 문제가 예측 하고자 하는 것은 continuous variable이다. (ex. 가격, 키, 몸무게 등) 하지만 continuous variable을 예측하고자 하는 것은 힘들기 때문에 분류를 많이 사용한다.
분류 문제는 예측하고자 할 때 분류를 많이 사용하고 이산적(카테고리) 데이터를 예측한다. 이때 데이터는 주로 binary(이진)로 많이 사용한다. 회귀와 분류의 차이는 "예측하고자 하는 것"이 다르다는 점이다.
예를 들어서 영화 리뷰에 대해서 생각해보면, 영화 리뷰는 별점을 총 5개까지 줄 수 있다. 분류 문제 입장에서 생각해보면 분류 문제는 보통 이진으로 많이 사용하기 때문에 정확도가 50%인데 별점을 총 5개까지 줄 수 있는 영화 리뷰를 분류로 예측하고자하면 정확도가 20%까지 떨어지게 된다. 때문에 이러한 경우에는 분류 문제로 할 이유가 없으므로 회귀로 문제를 해결하면 된다.
검증 데이터셋(Validate Dataset)
Logistic Regression에서는 검증 데이터 세트를 사용한다. 훈련 데이터는 모델을 Fit하게 만드는데 사용되고, 검증 데이터는 예측 모델을 선택하기 위해 예측의 오류를 측정할 때 사용되는 데이터 셋이다. 또한 hyper parameter로 튜닝한 효과를 확인하기 위해서 검증 데이터셋이 필요하다.
검증 데이터는 훈련 데이터만으로는 모델을 완전히 학습시키기 어렵기 때문에 검증 데이터셋으로 모델이 잘 학습되었는지 검증하고 모델을 선택하는 과정이 필요하다.
검증 데이터는 훈련 데이터의 일부분을 사용하며 훈련 데이터와 테스트 데이터를 나누는것과 동일하게 나눠준다.
from sklearn.model import train_test_split
# 훈련 / 테스트 데이터 7:3으로 나누기
train, test = train_test_split(df, train_size = 0.7, test_size = 0.3, random_state = 2)
# 훈련 / 검증 데이터 7:3으로 나누기
train, val = train_test_split(train, train_size = 0.7, test_size = 0.3, random_state = 2)기준 모델
분류 문제에서는 보통 타겟 변수에서 가장 빈번하게 나타나는 범주를 기준 모델로 설정한다. 타겟 변수가 편중된 범주 비율을 가지는 경우가 많으므로 항상 타겟 변수가 어떤 비율을 갖고 있는지 확인해봐야한다.
만약 타겟 변수가 클래스 1과 0의 비율이 2:8이라면 해당 모델은 0만 찍어도 정확도가 80%이므로 기준 모델은 정확도가 80%인 모델로 설정한 뒤 더 좋은 성능을 가지는 모델을 만들어야한다.
from sklearn.metrics from accuracy_score
# 타켓 데이터 범주 비율 확인
y_train = train[target]
y_train.value_counts(normalize = True)
# mode() : ~설명 추가 예정~
major = y_train.mode()[0]
# 타겟 샘플 수 만큼 0이 담긴 리스트를 만듬.
# 예제 기준으로 0이 더 많으므로 기준 모델의 범주(majority class)는 0이 된다.
y_pred = [major] * len(y_train)
print('training accuracy :', accuracy_score(y_train, y_pred))Odds (오즈)
Odds는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율로 성공 확률이 실패 확률에 비해 얼마나 더 높은지를 나타낸다.
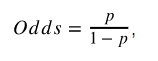
여기서 p는 성공 확률, 1-p는 실패 확률을 뜻한다. p가 1일때 odds는 양의 무한대가 되고, p가 0일 경우엔 odds도 0이 된다.
Logit Odds
Odds에 로그를 취해 변환하는 것을 로짓변환(Logit Transformation)이라고 한다. 로짓변환을 통해서 비선형형태인 Logist을 선형형태로 만들어서 회귀 계수의 의미를 편하게 해석하게 해준다. 기존의 Logstic 형태의 y값은 0~1의 범위를 가졌지만, 로짓은 음의 무한대에서 양의 무한대까지의 범위를 가지게 된다.
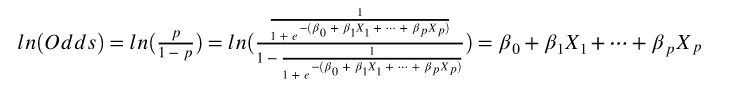
위의 식은 Logit Odds의 식으로 결과가 선형회귀의 식이 나오는 것을 확인할 수 있다.
Logistic Regression 모델 만들기
Logistic Regression은 앞서 배운 다른 회귀 모델들과 동일하게 sklearn에서 모듈을 가져와서 쉽게 모델을 만들 수 있다.
from sklearn.linear_model import LogisticRegression
logistic = LogisticRegression()
logistic.fit(X_train_data, y_train_data)
logistic.score(X_val_data, y_val_data)정확도를 높이기 위한 방법 ?
정확도를 높이기 위한 여러가지 방법들 중 내가 배운 것은 SimpleImputer와 StandardScaler이다.
SimpleImputer
SimpleImputer는 결측치를 처리하기 위한 것이다.
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy = 'mean')
X_train_imputer = imputer.fit_transform(X_train_data)
X_val_imputer = imputer.transform(X_val_data)StandardScaler
StanardScaelr는 특성들의 척도를 맞춰주기 위해서 표준정규분포로 표준화하는 것이다.
from sklearn.preprocessing import StanardScaler
scaler = StandardScaler()
X_train_scaler = scaler.fit_transform(X_train_imputer)
X_val_scaler = scaelr.transform(X_val_imputer)

