고유벡터와 고유값
선형 변환(Linear Transformation)
고유벡터를 설명하기 전에, 먼저 알아야 할 개념이 있는데 바로 선형 변환(Linear transformation)이다. 선형 변환은 임의의 두 벡터를 더하거나 혹은 스칼라 값을 곱하는 것을 말한다.
변환이 선형적이라는 것은 두가지 속성을 의미한다.
- 모든 선들은 변환 후에도 직선이어야 한다
- 원점은 변환 후에도 원점을 유지해야한다
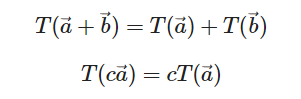
T가 위의 두가지 조건을 만족하면 T는 선형 변환에 해당한다.
↓↓ 강의를 들으면서 정리한 내용 ↓↓

고유 벡터(eigen vector)
행렬은 선형 변환 연산으로 벡터에 행렬을 곱하면 벡터의 크기도, 방향도 바뀐다. 이때 특정 벡터는 크기만 바뀌고 방향은 바뀌지 않는다. 이러한 벡터를 바로 고유 벡터(eigen vector)라고 한다.
쉽게 말해서 변환에 영향을 받지 않는 회전축을 공간의 고유벡터라고 부른다.
고유값(eigen value)
고유 벡터는 크기만 바뀌고 방향은 바뀌지 않는 벡터라고 위에서 언급했습니다. 이때 변화하는 크기는 결국 스칼라 값이 되는데 이 특정 스칼라 값을 고유값(eigen value)라고 한다.
↓↓ 강의를 들으면서 정리한 내용 ↓↓

이러한 고유값과 고유벡터는 numpy 라이브러리를 이용하면 굉장히 쉽고 빠르게 구할 수 있다 (라이브러리 만세🤘)
import numpy as np
x = [[1, 2], [3, 4]]
e_vector, e_value = np.linalg.eig(x)Principal Component Analysis(PCA)
주성분 분석은 고차원 데이터를 효과적으로 분석하기 위해서 낮은 차원으로 축소하는 기법이다.
PCA에 대해서 아직 아리송한 상태라서 구글링을 해보던 도중에 설명을 굉장히 깔끔하게 해놓은 블로그가 있어서 참고 링크로 가셔서 글을 한번 읽어보시는 것을 추천드립니다.
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
x = StandardScaler().fit_transform(x)
pca = PCA(n_components = 2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(
data = principalComponents,
columns = ['pc1', 'pc2']
)
# StandardScaler() : 평균을 제거하고 단위 분산에 맞게 조정해 기능을 표준화함
# fit_transform(x) : 데이터에 맞춘 다음 변환
# PCA(n_components = 2) : PCA를 해주는 메소드로 n_components는 주 성분을 몇개로 할 것인지 결정코드에서 pca를 진행하기 전에 데이터를 스케일링하는데 이는 데이터의 스케일에 따라서 주성분의 설명 가능한 분산량이 달라질 수 있기 때문이다.
위의 코드는 다음의 예제 코드 링크에서 일부분 가져온 것으로 위의 코드를 실행하기 전에 데이터를 불러오는 작업이 필요하다.

