기저벡터
벡터 공간의 기저는 공간 전체를 생성하는 선형독립인 벡터의 집합이다.
오른쪽을 가리키는 길이 1의 벡터를 x-단위벡터(크기(길이)로 1을 가지는 벡터를 단위벡터라고 부름), 위쪽을 가리키는 길이 1의 벡터를 y-단위벡터라고 한다. 두개를 통틀어서 좌표계의 기저(basis)라고 부른다.
선형 결합(Linear combination)
선형결합은 두 벡터를 스케일 하고 더해서 새 벡터를 얻는 모든 연산이다.
(선형 = 벡터끼리 스칼라배나 +로만 이뤄져 있는 것)
벡터 V가 벡터 V₁,V₂,...,Vn의 선형 결합이라는 것은 v = C₁V₁+ C₂V₂+...+CnVn을 만족하는 실수 C₁,C₂,...,Cn이 존재한다는 것이다.
이러한 벡터들의 선형 결합으로 만들 수 있는 모든 벡터들을 다 모아놓은 집합을 바로 span(생성)이라고 한다.
선형 독립(Linear independent)과 선형 종속(Linear dependent)
선형 독립은 V₁,V₂,V₃ 세개의 벡터가 모든 경우의 수에 있어서 선형 결합으로 표현되지 않는 것을 뜻한다.
풀어서 얘기하자면 V₁은 V₂의 선형 결합으로 표현되지 않고 V₂와V₃ 두개의 선형 결합으로도 표현되지 않는다. 이는 V₂와V₃도 마찬가지이므로 V₁,V₂,V₃은 선형독립적인 관계이다.
즉, 집합 S = { V₁,V₂,V₃, ..., Vn}의 벡터들은 C₁V₁,C₂V₂,C₃V₃, ...,CnVn = 0 (영벡터)을 만족하는 계수들이 C₁= 0, C₂= 0, C₃= 0, ... , Cn = 0 이외에 존재하지 않을 때 "선형적으로 독립이다" 라고 한다.
공분산
공분산은 2개의 확률변수의 선형관계를 나타내는 값이다. 1개의 변수 값이 변화할 때 다른 하나의 변수가 어떠한 연관성을 나타내며 변하는지를 측정한다.
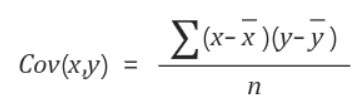
공분산은 x의 편차와 y의 편차를 곱한 것의 평균값이다.
공분산이 0보다 크면 x가 증가할 때 y도 증가하게 된다.
공분산이 0이면 두 변수간 아무 상관 관계가 없다. 즉, 독립적이다.
0보다 작을 경우에는 x가 증가하면 y는 감소하게 된다.
공분산은 확률변수의 단위 크기에 영향을 많이 받기 때문에 이를 보완할 수 있는게 바로 상관계수이다.
공분산은 numpy.cov 메소드를 통해서 쉽고 빠르게 얻을 수 있다.
numpy.cov(array_like)
상관계수
상관계수는 두 변수 사이의 통계적 관계를 표현하기 위해서 특정한 상관 관계의 정도를 수치적으로 나타낸 계수이다.
상관계수는 -1에서 1까지로 정해진 범위 안의 값만 가지며 선형 연관성이 없으면 0에 근접하게 된다.
상관계수는 numpy.corrcoef 메소드를 통해서 쉽고 빠르게 얻을 수 있다.
numpy.corrcoef(array_like, y = None, rowvar = True, dtype = None)번외) 오늘 사용한 함수들
맨날 사용한 함수를 어떻게 사용하는지를 까먹어서 한줄로 간단하게 함수들을 정리하려고 한다! 오늘은 공분산, 상관계수를 구하는 함수를 포함해서 총 6개 정도의 함수를 사용했다. 위에서 서술한 corrcoef와 cov 함수는 제외한 나머지 함수들을 정리해봤다.
numpy.var
numpy.var(array_like, axis = None, dtype = None)
# array_like => 배열과 유사한 자료형 예를 들면 리스트, 튜플, np.array 등이 있다.
# 분산을 계산해 주는 함수numpy.std
numpy.std(array_like, axis = None, dtype = None)numpy.multiply
numpy.multiply(x, y)
# x, y는 각각 array_like가 들어간다
# x와 y의 인수들을 곱해주는 메소드
x = [1, 2, 3]
y = [4, 5, 6]
res = numpy.multiply(x, y)
# res = [4, 10, 18]
# res = [1·4, 2·5, 3·6]numpy.linalg.matrix_rank
numpy.linalg.matrix_rank(array_like)
# 행렬의 rank를 계산해주는 메소드
# rank란? 행렬의 열들로 생성될 수 있는 벡터의 공간 차원을 말함. 간단하게 행렬의 계수라고 볼 수 있음
