분할 정복 (Divide and Conquer)

분할 정복은 복잡하거나 큰 문제를 작은 문제들로 나눠서 문제를 해결하는 방법으로 병렬적으로 문제를 해결할 수 있다는 특징을 갖고 있다.

분할 정복의 진행 방식은 분할, 정복, 병합 세단계로 나눌 수 있다.

• (1) 분할: 큰 문제를 작은 문제들로 분할
• (2) 정복: 재귀적으로 작은 문제들을 해결
• (3) 병합: 해결된 결과를 사용해 큰 문제를 해결

# 분할정복 의사코드
def F(x):
  if F(x)의 문제가 간단 then:
    return F(x)을 직접 계산한 값 # Conquer ==> result
  else:
    x를 y1, y2로 분할
    F(y1)과 F(y2)를 호출
    return F(y1), F(y2)로부터 F(x)를 구한 값 # combine => conquer & merge

퀵 정렬 (Quick Sort)

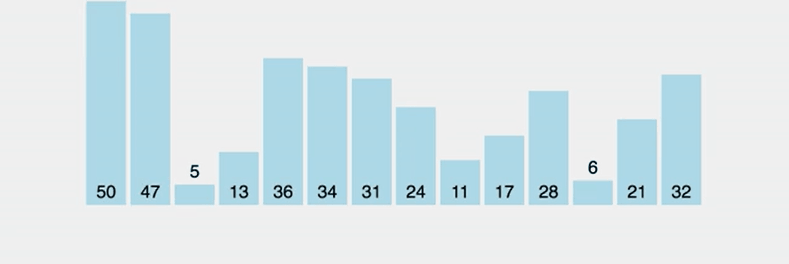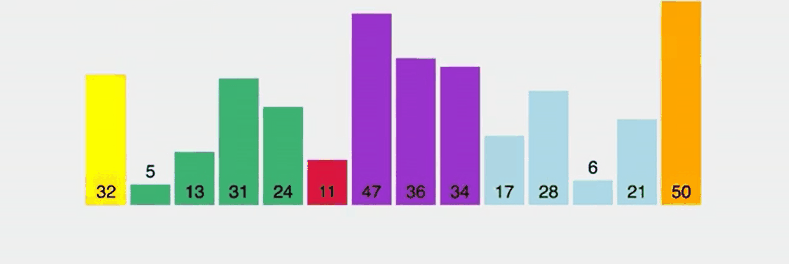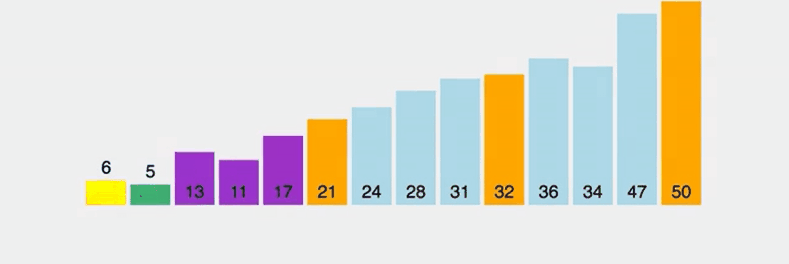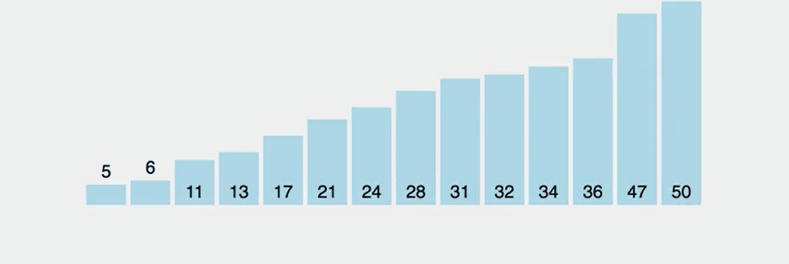
퀵 정렬은 빠른 속도로 정렬할 수 있는 알고리즘으로 분할 정복 방법을 사용한다. 퀵 정렬은 배열 중에서 pivot이라는 노드를 하나 고른 뒤 pivot 앞에는 pivot보다 작은 값이, 뒤에는 큰 값을 가진 노드가 오도록 나눠준다. 그리고 분할된 두 배열 (작은값 / 큰값) 에 대해서 재귀적으로 위의 과정을 반복해준다.

quick sort.gif

위의 gif에서 노란색 노드는 pivot 노드, 초록색 노드는 pivot 노드보다 작은 노드, 보라색 노드는 pivot 노드보다 작은 노드, 주황색 노드는 정렬이 완료된 노드로 생각하고 보면 이해하기 쉽다.

퀵 정렬을 최선의 경우에는 O(nlogn)의 시간 복잡도를 가지지만 최악의 경우에는 O(n²)의 시간 복잡도를 가지게 된다. 평균적으로는 O(nlogn)의 시간 복잡도를 가진다.

def quick_sort(li):
    li_length = len(li)
    
    if li_length <= 1:
        return li
    else:
        pivot = li[0]
        greater = [x for x in li[1:] if x > pivot]
        lesser = [x for x in li[1:] if x <= pivot]
        return quick_sort(lesser) + [pivot] + quick_sort(greater)

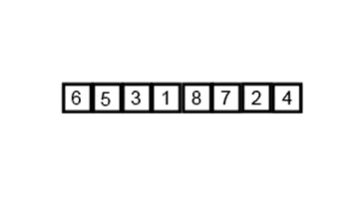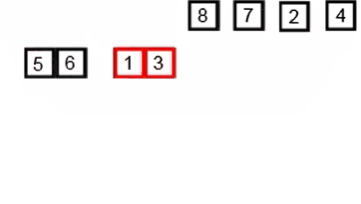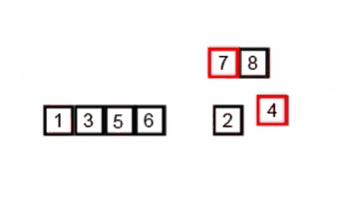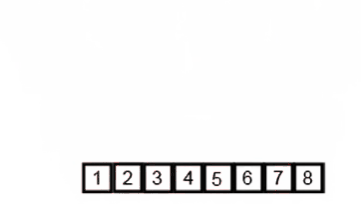
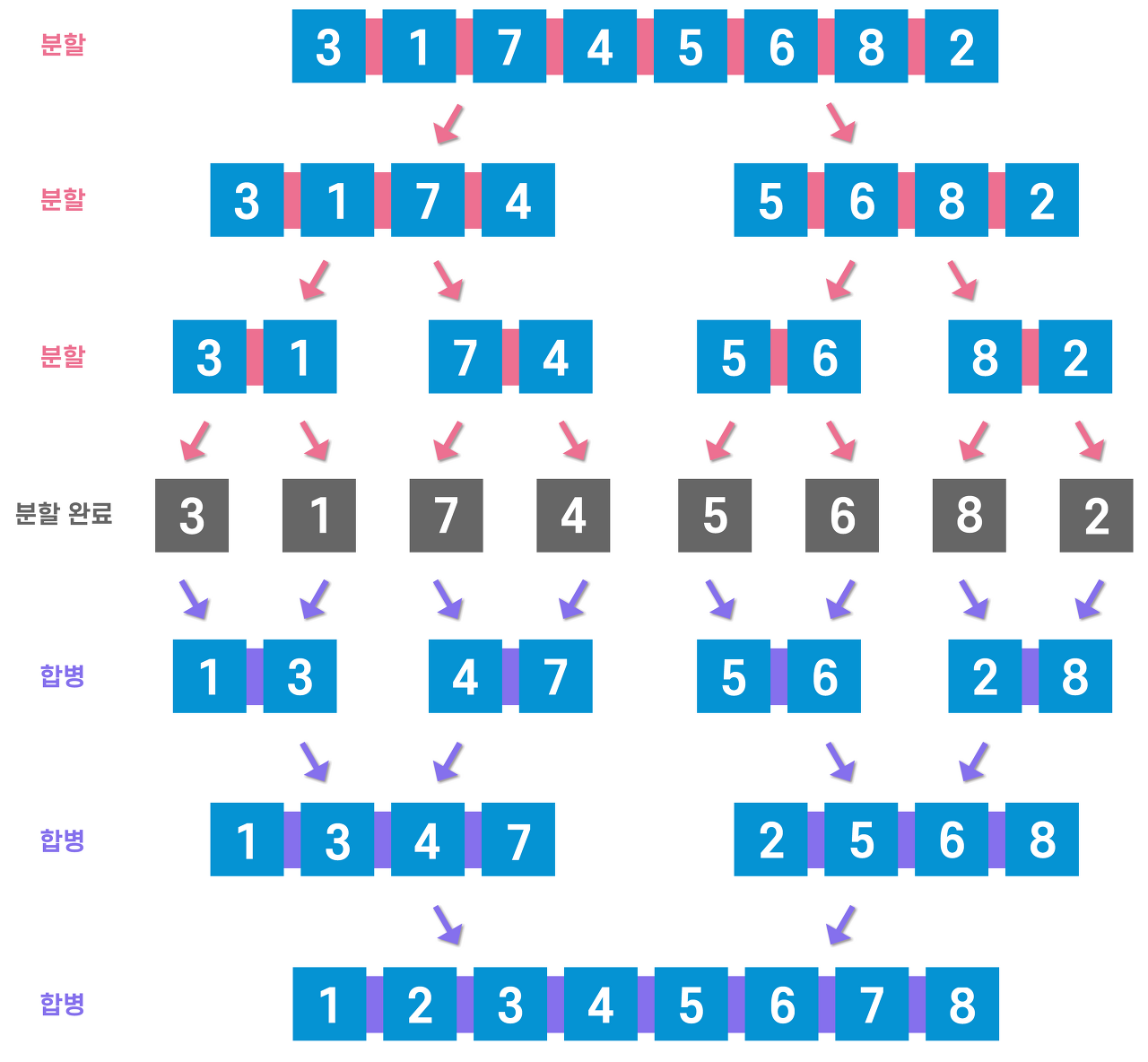
병합 정렬 (Merge Sort)

병합 정렬 또한 분할 정복 방법을 사용한 알고리즘이다. 우선 배열을 더이상 분할할 수 없을 때까지 나눠준다. 그 뒤 작게 나뉜 요소들의 대소를 비교해 합쳐주는 과정을 반복한다. 병합 정렬의 경우 O(nlogn)의 시간 복잡도를 가진다.

merge sort.gif

merge sort

# 리스트를 합쳐주는 함수 
def merge(left, right):
    res = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    
    res.extend(left[i:])
    res.extend(right[j:])
    
    return res

# 병합 정렬 함수
def merge_sort(li):
    length = len(li)
    
    if length == 1:
        return li
    
    mid = length // 2
    
    left = merge_sort(li[:mid])
    right = merge_sort(li[mid:])
    
    return merge(left, right)