다중 선형 회귀(Multiple Linear Regression)
다중 선형 회귀는 어제 배운 선형 회귀 모델과 크게 다르지 않다. 다른점은 딱 한가지 있는데 그건 바로 선형회귀모델은 feature를 하나만 쓴다는 점이고, 다중선형회귀는 feature를 여러개 쓸 수 있다는 점이다. 때문에 선형회귀보다 좋은 성능을 갖고 있다.
선형회귀의 식은 y = b₀ + b₁x 으로 표현할 수 있고, 다중선형회귀의 식은 y = b₀ + b₁x₁ + ... + bₙxₙ 으로 표현된다. 다중선형회귀의 식은 추가되는 feature의 수만큼 bₙxₙ의 수가 늘어나게 된다.
다중선형회귀 모델 만들기
from sklearn.linear_model import LinearRegression
model = LinearRegression()
target = ['타켓']
features = ['특성1', '특성2']
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = test[target]
# 모델 fit 후 test data에 적용
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 다중선형회귀 회귀식
b0 = model.intercept_
b1, b2 = model.coef_
print(f'y = {b0:.0f} + {b1:.0f}x + {b2:.0f}x')위의 코드를 실제로 적용했을 때, 아래와 같은 결과가 나오게 된다.
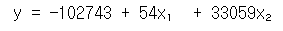
회귀모델을 평가하는 평가지표(evalation metrics)
MSE(Mean Squared Error)
MSE를 구하는 식은 다음과 같다.
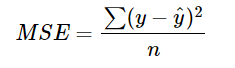
MSE는 sklearn.metrics로 간단하게 사용할 수 있다.
from sklearn.metrics import mean_squared_error
mse = mean_squared_errir(y_test, y_pred)RMSE(Root Mean Squared Error)
RMSE는 MSE에 루트를 씌워서 사용하며, 오류 지표를 실제 값과 유사한 단위로 다시 변환해 해석을 쉽게 한다. 일반적으로 rmse 수치가 낮을 수록 정확도가 높다고 판단한다.
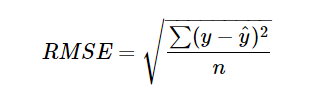
rmse = mse ** 0.5
MAE(Mean Absolute Error)
MAE는 다음과 같이 정의되며, 모델의 예측값과 실제값의 차이를 모두 더하는 방식을 취하고 있다.
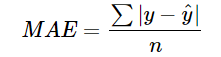
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_test, y_pred)R-squared (R²)
R-squared는 적합도를 측정하는 방법이다. 실제 값과 실제 값의 평균 거리까지의 거리를 취한 뒤 이를 추정값과 비교하는 과정이다.
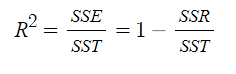
SSE(Sum of Squares Error)
추정값에서 관측값의 평균 혹은 추정치의 평균을 뺀 결과의 총합을 뜻한다.
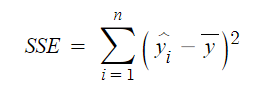
SSR(Sum of Squares due to Regression)
관측값에서 추정값을 뺀 값으로 잔차의 총합이라고 부른다.
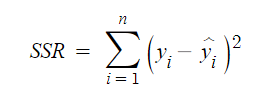
SST(Sum of Squares Total)
관측값에서 관측값의 평균 혹은 추정치의 평균을 뺀 결과의 총합을 뜻한다.
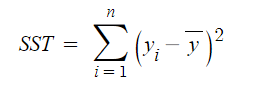
위의 내용들을 쉽게 정리해서 예를 들자면 다음과 같다. 예를 간단하게 들기 위해서 어제 구했던 선형회귀식의 값을 재활용하기로 했다.
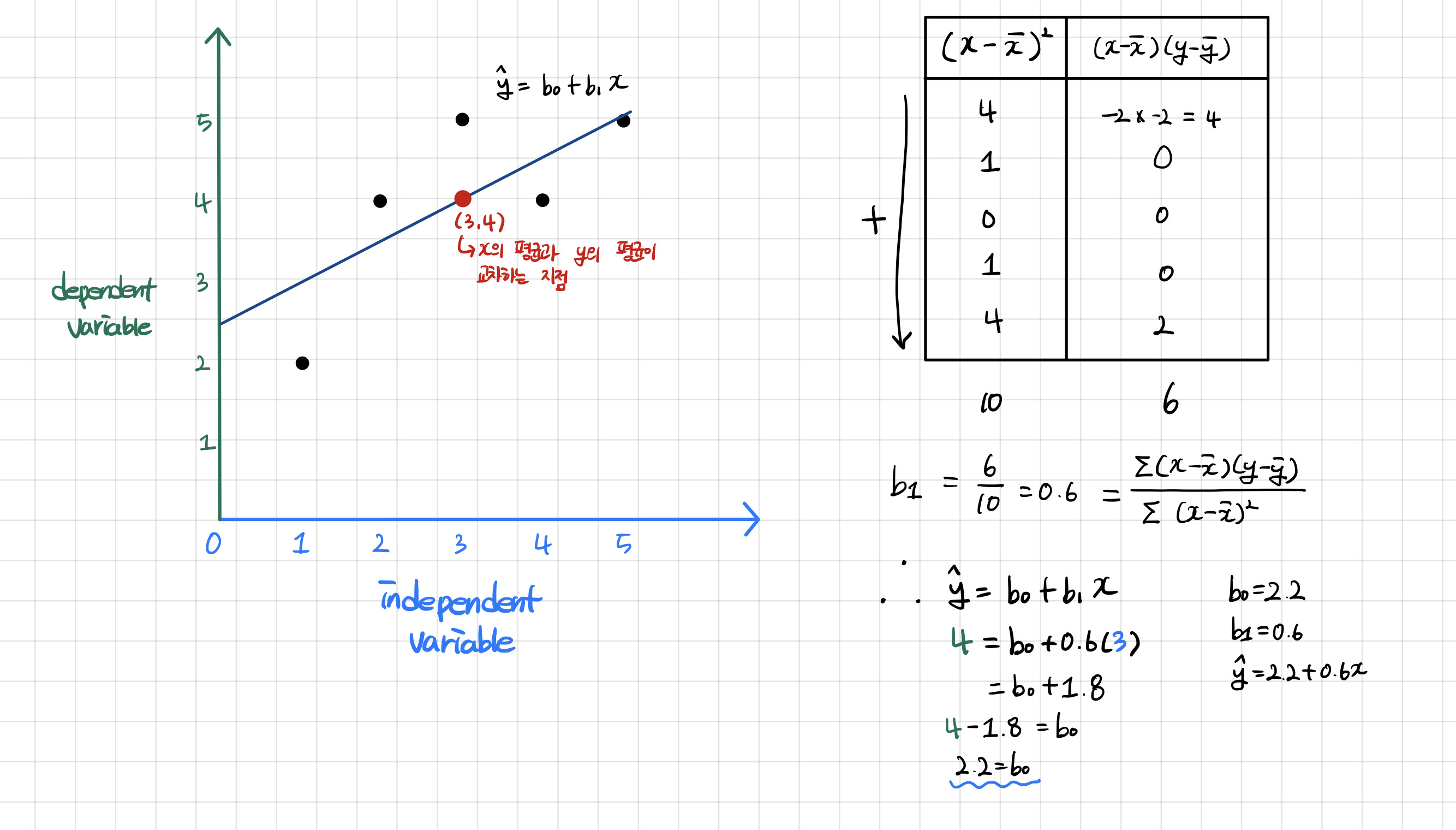
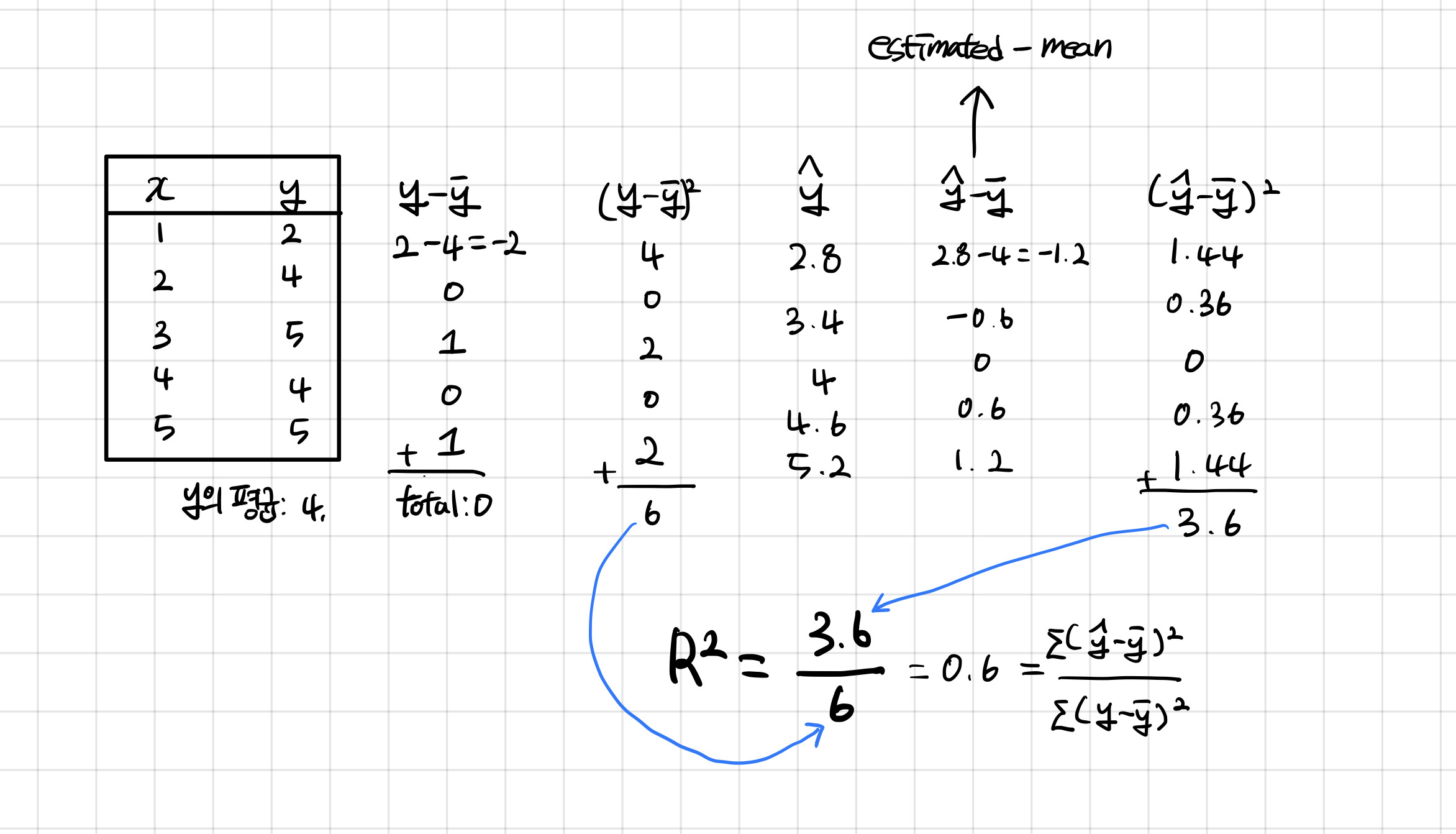
여기서 (y - y-bar)²이 바로 분모로 들어가는 SST이고, (y-hat - y-bar)²이 바로 분모로 들어가는 SSE이다.
과적합(Overfitting)과 과소적합(Underfitting)
과적합과 과소적합을 알기 위해서는 일반화(generalization)에 대해서 먼저 알아야 한다.
테스트데이터셋에서 만들어내는 오차를 일반화 오차라고 부르며, 훈련 데이터셋에서처럼 테스트데이터셋에서도 좋은 성능을 내면 일반화가 잘 된 모델이라고 한다.
과적합은 모델이 훈련 데이터셋에서만 특수한 성질을 과하게 학습해버려서 일반화를 못해 결국 테스트데이터가 커지는 현상을 뜻한다. 여기서 과하게 학습을 한다는 것은 회귀선이 아래와 같이 모든 데이터를 찾아내서 통과하려고 하는 것이다.
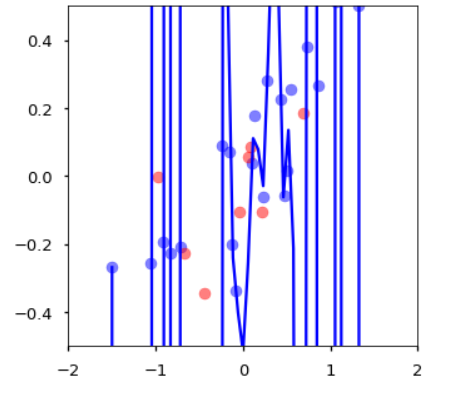
과소적합은 과적합과 만대로 훈련 데이터에 과적합도 못하고 일반화 성질도 학습하지 못해서 훈련 데이터에도, 테스트 데이터에서도 모두 오차가 크게 나오는 경우를 말한다. 이를 쉽게 말하면 너무 단순한 모델이 생성되어서 학습 데이터와 잘 맞지 않는 경우를 과소적합 됐다고 한다.
편향-분산 트레이드 오프(Bias-Variance Trade Off)
과적합과 과소적합은 오차의 편향(Bias)와 분산(Variance)와 관계가 있다. 이때 편향은 일반화 오차 중에서 잘못된 가정으로 인한 것이고, 분산은 훈련 데이터에 있는 작은 변동에 모델이 과하게 민감하게 반응하여 나타나는 것이다.
분산이 높은 경우는 학습 데이터의 작은 변동에 모델이 과하게 민감하게 반응을 하기 때문에 일반화를 잘 못하는 경우, 즉 과적합 상태이다.
편향이 높은 경우는 학습 데이터의 특성과 타겟 변수의 관계를 잘 파악하지 못해서 일반화를 하지 못한 경우, 즉 과소적합 상태이다.
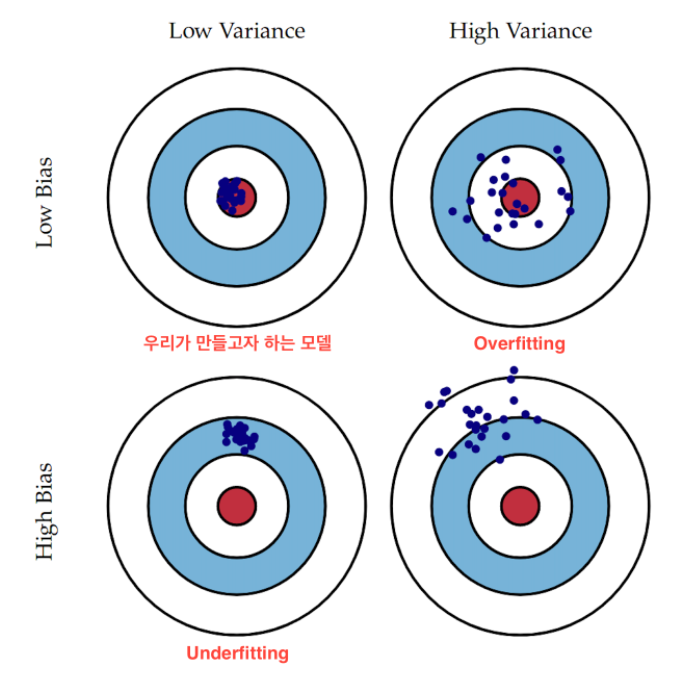
위의 그래프에서 Los Bias/High Variance의 경우 예측 결과가 실제 결과에 비교적 근접해보이지만 꽤 넓게 분포되어 있는데 이를 과적합된 것이라고 볼 수 있다. 반면 High Bias/Low Variance의 경우는 정확한 결과값을 하나도 맞추지 못하고 특정 부분에만 예측이 집중되어 있는 것을 볼 수 있다. 이는 학습 데이터가 학습을 제대로 하지 못했다는 것이고 과소적합된 것이라고 볼 수 있다.

