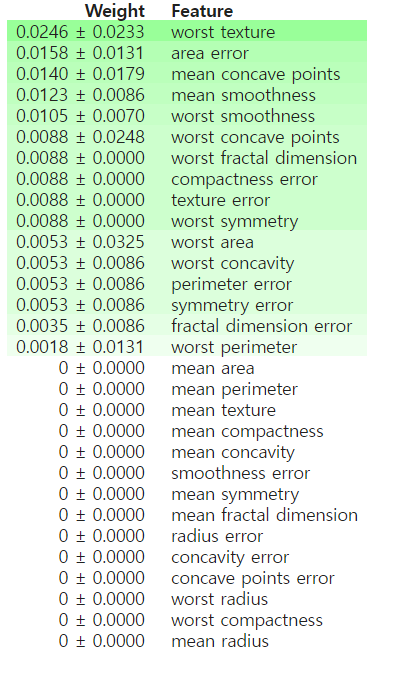
순열 중요도(Permutation Importances)

순열 중요도는 한번에 한개의 특성 값을 섞은 후 특성과 실제 결과 사이의 관계를 없앤 뒤 모델의 예측 오차 증가를 측정하는 방법이다.
특성값을 섞었을 때 모델의 오류가 증가한다면 해당 특성은 중요한 특성이라고 해석할 수 있고, 모델의 오류가 증가하지않고 비슷하다면 해당 특성은 중요하지 않은 특성이라고 해석할 수 있다.

python에서는 eli5라는 라이브러리를 사용해서 show_weights 메소드를 이용하면 아래와 같이 편리하게 결과를 볼 수 있다.

XGBoost

XGBoost에 대해서 정의하기 전에 AdaBoost, Gradient Boost에 대해서 알고 넘어가면 좋을 것 같아서 정리를 했다.

먼저 Boost란 머신러닝에서 성능이 낮은 weak learner들을 하나의 강력한 strong learner로 변환시키는 방법을 말하며 가장 널리 쓰이는 알고리즘은 AdaBoost와 Gradient Boost가 있다.

AdaBoost

AdaBoost는 결정 트리에서 각 관측값에 같은 가중치(weight)을 주고 훈련을 시키는 방법이다. AdaBoost에서는 stump를 사용하는데 여기서 stump란 아래의 그림처럼 노드 하나에 두개의 리프를 가진 트리를 뜻한다.

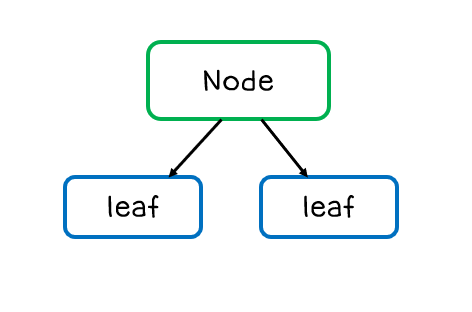
AdaBoost는 이러한 Stump들로 구성되어 있어서 Forest of Stumps라고 한다. 트리와 다르게 stump는 정확한 분류를 하지 못하기 때문에 wek learner이다.

그리고 각 stump에 가중치를 줌으로써 결과에 영향을 더 크게 미치는 stump가 생기게 된다. 모든 stump들은 처음에는 같은 가중치를 갖고 시작하지만, 첫번째 모델이 잘 분류를 하지 못하는 데이터에게는 가중치를 조금 더 부여한다. 때문에 두번째 모델에서는 첫번째 모델에서 잘 분류하지 못했던 데이터가 조금 더 잘 분류가 된다. 이러한 과정이 계속 반복되면서 최종적으로는 성능이 좋은 분류기를 만들게 되는 것이다.

Gradient Boost

앙상블 방법의 부스팅의 대표적인 모델이 바로 위에 정리를 한 AdaBoost와 Gradient Boost 등이 있다. Gradient Boost는 회귀와 분류 문제에 모두 사용할 수 있는 모델이다.

AdaBoost와 Gradient Boost의 차이점은 AdaBoost는 분류하기 어려운 값들에 대해서 가중치를 주는 방식으로 약점을 파악했다면, Gradient Boost는 비용함수를 이용해서 잔차들을 구분한다는 점이다.

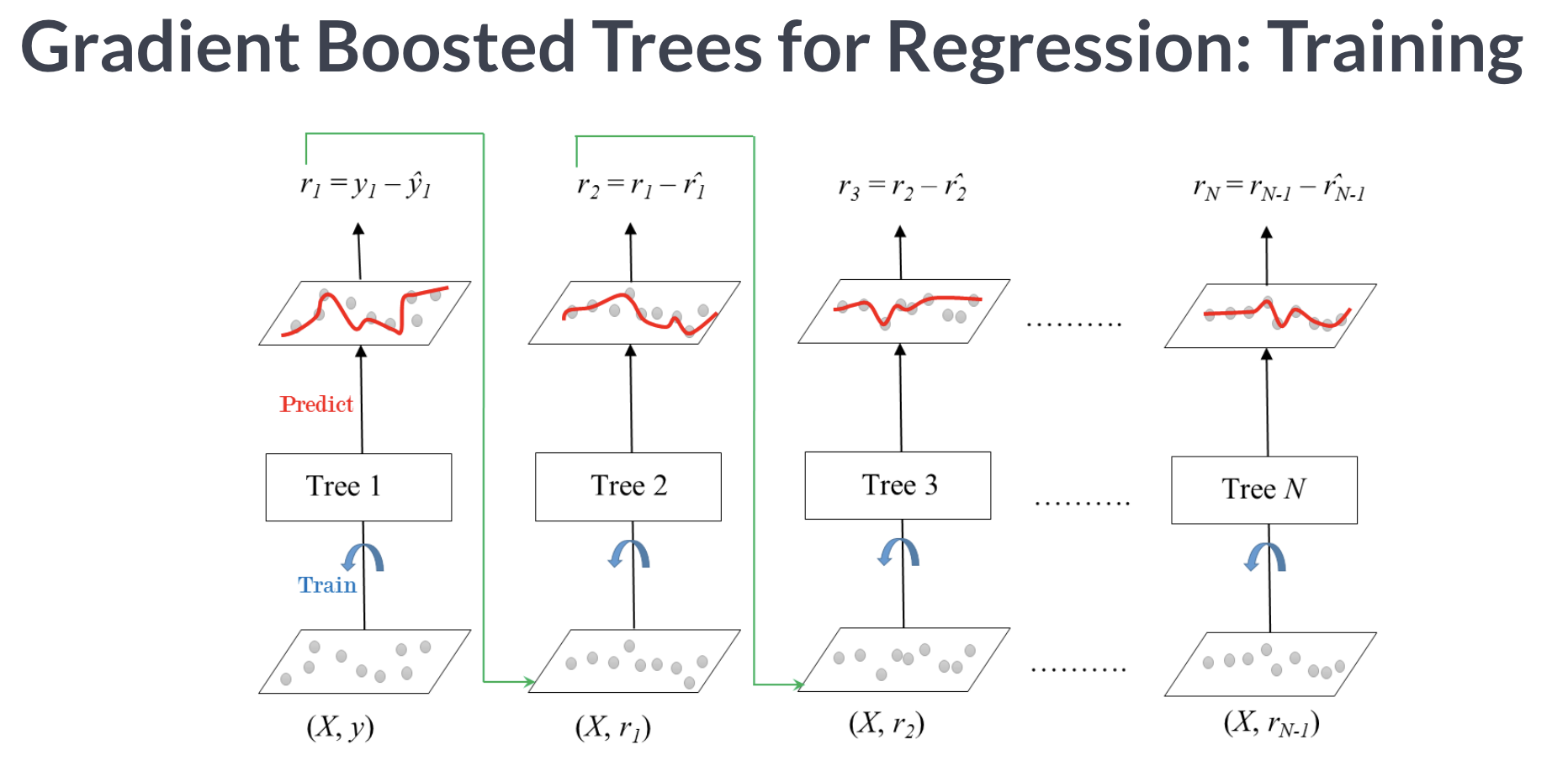
Tree 1을 통해서 y를 예측하고 남은 잔차를 다시 Tree2를 통해서 예측하고 Tree1 + Tree2 모델을 통해서 y를 예측하면 Tree1보다 나은 Tree2를 만들 수 있게 된다. 이러한 방법을 반복하다보면 잔차는 점점 줄어들게 되지만 과적합이 일어날 수도 있다는 단점도 갖고 있다.

XGBoost

XGBoost는 Gradient Boost가 병렬학습이 지원되도록 구현한 라이브러리이다. XGBoost도 회귀와 분류 문제를 모두 지원해주며, 성능과 효율이 좋아서 많이 쓰이는 알고리즘 중 하나이다.

XGBoost는 Gradient Boost에 비해서 수행 시간이 빠르고, Gradient Boost의 단점이었던 과적합을 규제해준다. 또한, 분류와 회귀영역에서 뛰어난 예측 성능을 발휘한다는 장점도 있다.

XGBoost는 sklearn에서도 라이브러리를 제공해주지만 속도가 느릴 수도 있다는 단점이 있어 xgboost에서 제공해주는 라이브러리를 사용하면 좋다는 얘기를 주워들었습니다.

이 모델에는 Eaerly Stopping이라는 기능이 있는데 이 기능을 사용해서 과적합을 피할 수 있다.

model = XGBClassifier(
	n_setimators = 200,
   max_depth = 7,
   n_jobs = -1
)

model.fit(X_train, y_train, early_stopping_rounds = 50)

#early_stopping_rounds = 50은 50 rounds 동안 스코어의 개선이 없으면 멈춘다는 이야기이다.