• Physically based rendering으로 현실 세계와 더 일치하도록 하는 모델이다.
• Phong 및 Blinn Phong과 비교했을때 더 현실적으로 보인다.
• 현실의 근사치이기때문에 Physical shading이 아니라 physically based shading이라고 함
• 다음의 3가지 조건을 충족 해야한다
  1. microfacet 표면 모델을 기반
  2. 에너지를 보존
  3. 물리적 기반 BRDF를 사용
• PBR 방정식

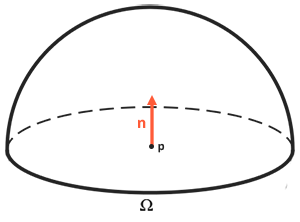
• 관측자가 점 $p$ 를 $w_o$ 방향으로 보았을때의 Radiance $L_o(p,\omega_o)$는 반구 $\Omega$로 $w_i$ 방향으로 들어오는 빛의 Radiance를 모드 합한것
• 표면에 직각으로 빛이 들어올때 가장 강한데 이를 표현하는 식이 $n\cdot w_i$ 입니다.
• $f_r(p,w_i,w_o)$ 는 BRDF식이다.

The microfacet model

• 모든 PBR 기술은 microfacet 이론을 기반으로 한다.
• microfacet이론은 표면을 아주 크게(microscopic scale)봤을때 모든 표면이 microfacet이라고 매우 작은 반사되는 거울과 같다는 이론이다.
• Roughness에 따라 얼마나 반사되는지에 따라 차이가 많이 난다.

• 위 그림과 같이 거친 표면은 빛이 서로 완전히 다른 방향으로 반사되지만 매그러운 표면은 대부분 같은 방향으로 반사된다.
• 거친 표면은 반사가 흐리게, 매끄러운 표면은 반사가 뚜렷하게
• microscopic scale 로 봤을 때는 어떤 표면도 완벽하게 매끄럽지 않다. PBR 모델은 이런 표면을 표현하기위해 roughness map이라는 것을 사용하고 픽셀마다 거친정도를 나타낸다.
• 이 값을 가지고 Blinn-phong shasding에서 사용된 half vector와의 각을 계산해서 각이 작을수록 빛의 반사가 뚜렷하고 강하고, 클 수록 빛의 반사가 흐리고 퍼진다.
• microfacet는 통계적으로 근사할수있다.

Energy conservation

• Microfacet 근사법은 에너지 보존의 법칙을 따른다.
• 에너지 보존이란 나가는 에너지와 들어오는 에너지의 량이 동일한 것
• 이런 에너지 보존 원칙을 나타내기 위해 specular와 diffuse의 뚜력한 구분이 필요하다.
• 빛이 표면에 닿을때 굴절과 반사가 두 종류가 나누니다.
• reflection : 빛이 표면에 닿앗을때 바로 반사하고 표면안으로 들어가지 않는다 → specular lighting
• refraction : 빛이 표면에 닿았을때 표면에 들어가 흡수 → diffuse lighting

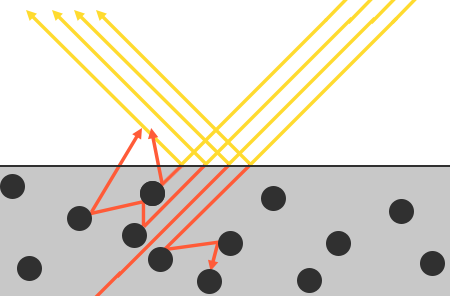
• 굴절된 모든 빛이 흡수 되지는 않는다. 빛은 입자들과 충돌할때마다 무작위 방향으로 산란하다가 에너지를 다 사용하거나, 표면 밖으로 다시 나갈때까지 전진한다. 다시 표면으로 나가는 빛은 표면의 색상에 영향을준다.
• Subsurface Scattering : PBR에서 굴절된 모든 빛은 흡수되고 매우 작은 영역에서만 산란되도록하는 기법
• 입사된 빛의 세기는 굴절된 빛의 세기와 반사된 빛의 세기의 합과 같다

BRDF

• BRDF(양방향 반사 분포 함수, Bidirectional Reflectance Distribtion Function)
• 표면의 반사 속성을 표현하는 함수
• BRDF가 물리적으로 타당해지기 위해서는 에너지 보존과 전시 상반성(exhibit reciprocity)를 갖춰야한다.
• 상반성은 들어오는 빛과 나가는 광선이 BRDF의 결과에 영향을 주지 않으면서 서로 상반된다는 헬름홀츠 상반원리를 말한다.
• BRDF는 들어는 빛의 방향$\omega_i$ 나가는 빛의 방향 $\omega_o$, 표면의 노말 n, 표면의 파라미터 a를 입력으로하는 함수
• 이를 입력으로 하여 물질의 특성을 고려하여 불투명한 표면의 최종 반사광에 얼마나 많은 기여를 했는지 결과로 계산
• 표면이 거울과 같은 완전히 매끄러문 표면이라면 BRDF함수는 모든 $\omega_i$에 대하여 0을반환, $\omega_o$에 대해 1을 반환

Cook-Torrance BRDF

• Cook-Torrance BRDF는 Robert L.Cook과 kenneth E.Torrace에 의해 개발되엇다.
• 기존의 Phong이나 Blinn phong모델이 비교하여 에너지 보존 법치과 미세표면이론을 도입하여 더욱 물리적인현상을 기반으로하는 리얼리티를 가능하게 함.
• Cook-Torrance BRDF 식은 다음과 같으 diffuse와 specular로 나뉜다.

• $k_d$는 들어오는 빛의 비율이며, $k_d$는 반사되어 나가는 빛의 비율

diffuse($f_{lambert}$)

• $f_{lambert}$ 는 램버트 반사율을 표현
• 물체 표면의 휘도가 등방성을 가질때를 의미한다.

• c 는 Albedo 또는 표면의 색, 보통 물체의 색을 표현하는 Albedo texture에서 값을 받아옴
• 위의 식을 PBR 방정식에서 램버트만을 고려한면

이때 $k_d$ 와 $f_{lambert}$는 적분과 관계없으므로 앞으로 나올수 있다.

즉 $f_{lambert}$는

$n \cdot w_i$ 에서 $n$과 $w_i$ 는 길이가 1로 정규화하여 쓰기 때문에 $cos\theta$로 바꿀수있다.

따라서

Specular($f_{cook-torrance}$)

• Cook-Torrance의 Specular BRDF는 3가지 함수와 이를 정규화하는 계산을 이루어진다.
• Normal Distribution Function : 표면의 거칠기에 따라 Microfacet들이 얼마나 H벡터와 정렬되는지 계산
• Geometry Function : Microfacet으로 인한 Occulusion으로 shadowing과 Masking이 발생해 표면이 반사하는 빛의 양이 줄어든다.
• Fresnel Equation : 서로 다른 각도의 표면에서 반사되는 빛의 비율

D : Trowbridge-Reitz GGX

$h$ : 표면의 거칠기의 척도인 microfacet을 측정하기 위한 중간 벡터

$n$ : normal

$\alpha$ : roughness의 제곱

D는 표면의 microfacet들 중 H 벡터에 정확히 정렬된 Microfacet들이 얼마나 있는지 통계적으로 근시한 함수

• roughness 가 높아 질수록 specular의 강도가 약해지고 퍼지게 된다

float distributionGGXTR(vec3 normal, vec3 halfDir, float roughness){
	float alpha = roughness * roughness;
	float alpha2 = alpha * alpha;
	float NdotH = saturate(dot(normal,halfDir));
	float num = alpha2;
	float denom = PI * pow(NdotH*NdotH*(alpha2-1)+1,2);

	return num/denom;
}

G : SchlickGGX + SmithsMethod

• G는 표면의 Microfacet들이 서로 겹쳐서 빛이 차단되는 영역을 통계적으로 근사한 함수

$n$ : normal

$v$ : view vector

$k ={ (Roughness +1)^2\over 8}$

float geometrySchlickGGX(vec3 normal, vec3 v, float roughness){
	roughness+=1;
	k = (k*k)/8.0;
  float NdotV = saturate(dot(normal,v));
	float num = NdotV;
	float denom = NdotV * (1-k)+k;
	return num/denom;
}

• 표면을 효과적으로 근사하기 위해서는 관찰자가 바라보는 방향인 $v$와 빛의 방향인 $l$ 을 모드 고려해한다.
• Smiths의 방법을 이용하여 해결할수 있다.

float geometrySmithMethod(vec3 normal, vec3 viewDir, vec3 lightDir, float roughness){
	float viewSub = geometrySchlickGGX(normal,veiwDir,roughness);
	float lightSub= geometrySchlickGGX(normal,lightDir,roughness);
	return viewSub * lightSub;
}

F : Schlick Approximation

• F는 표면을 보는 각도에 따라 빛을 얼마나 반사할지 정하는 함수.

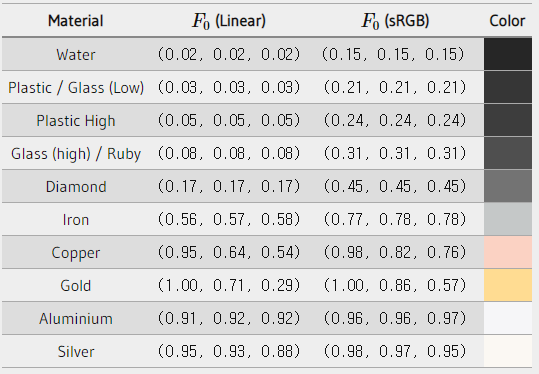
                                                     Naty Hoffman의 코스 노트

• 물체에따른 $F_0$ 값

$F_0$ : 표면의 반사율이다, 보통 $IOR$을 1.5로 사용하는데 이를 계산하면 $F_0$=0.04가 된다.

vec3 fresnelSchlickApproximation(vec3 F0, vec3 viewDir, vec3 halfDir){
	float HdotV = saturate(dot(halfDir,viewDir));
	return F0 + (1.0-F0)*pow(1.0-HdotV,5);
}

위의 과정들을 모두 합해서 PBR식에 대입하면

• $f_{cook-torrance}$부분 앞에 $k_s$가 없는데 이는 $F$가 표면에서 반사되는 빛의 비율울 나타내기 때문이다