시간복잡도
1. 입력의 개수가 n일 때, 시간 복잡도 함수 T(n)의 관계는 상당히 복잡할 수 있습니다.
Ex) T(n) = n^2 + n + 1
2. 그런데, n의 값이 클 수록 n^2 + n + 1에서 n+1 의 비중은 미미합니다.
Ex) n =1000 일 때, n^2(100만) + n(1000) + 1 이 되는데
n^2 의 비중이 99.9%
3. 빅오 표기법은 시간 복잡도 함수의 증가에 별로 기여하지 못하는 항을 생략합니다.
Ex)T(n) = n^2 + n + 1
에서 n+1 을 생략하고 n^2만 남겨서
O(n^2) 이 됩니다.
(1, 2, 3번 항목의 내용은 천인국, 공용해, 하상호 저자님들의 C언어로 쉽게 풀어쓴 자료구조 개정 3판을 참고했습니다.)
4. 빅오의 그래프를 잠깐 보시겠습니다
x축은 입력한 데이터의 크기 n이고
y축은 알고리즘을 수행하는 데 걸리는 빅오 O( )를 나타냅니다.
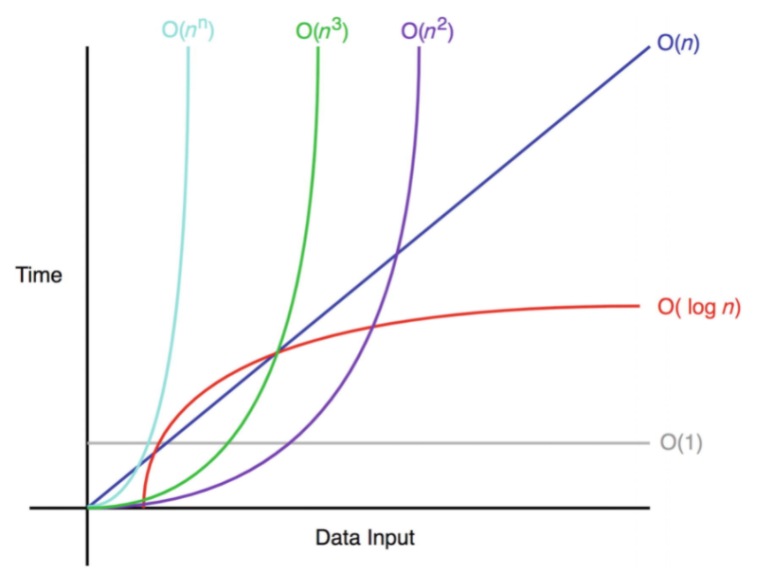
이미지 출처: https://velog.io/@zxcvbnm5288/Nov.-10-2020-Big-O-natation빅오-표기법
속도는
O(1)이 제일 빠르고
O(1) > O(logn) > O(n) > O(n^2) > O(n^3) > O(n^n)
순서대로 빠른 것을 알 수 있습니다.
5. 소스코드에서 빅오를 파악할 수 있다면
소스코드의 시간복잡도를 파악하고,
더 빠른 소스코드를 짤 수 있는 시야가 생긴다는 것입니다.
6. 소스코드를 보여드릴테니,
시간복잡도 함수 T(n) 과 빅오를 같이 파악해보아요
해설과 정답은 주석에 있습니다!
#include<stdio.h>
#include<windows.h>
int main()
{
int i = 0;
int n = 0;
printf("데이터 n개를 입력하세요\n");
scanf("%d", &n);
printf("n이 몇개든 곧바로 실행되면 O(1)\n");
for (i = 0; i < n; i++)
{
Sleep(1000); //1초동안 멈춤
}
printf("데이터 n을 입력할 때 n번의 루프 후 실행 완료되면 O(n)\n");
for (i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
Sleep(1000); //1초동안 멈충
}
}
printf("데이터 n을 입력할 때 n^2번의 루프 후 실행 완료되면 O(n^2)\n");
//시간복잡도 함수로 T(n) = n^2 + n + 1;
//빅오 O(n^2)
//n이 1000이면 n^2(1000000)초 + n(1000) 초 + 0초가 걸린다.
//n이 클 수록 n+1의 비중은 미미하므로, 시간 복잡도 향상에 기여하지 못하는 항은 생략하는 것
}
참고링크: https://velog.io/@zxcvbnm5288/Nov.-10-2020-Big-O-natation빅오-표기법
참고서적: 천인국, 공용해, 하상호, [C언어로 쉽게 풀어쓴 자료구조 개정 3판], 생능출판