Machine Learning with PyTorch and Scikit-Learn_chapter5

chapter 5 Compressing Data via Dimensionality Reduction

feature extraction을 통한 dimensionality reduction에 대해 배움.

• dimensionality reduction 관점에서 feature extraction은 관련된 정보를 대부분 유지하면서 data compression.
  feature selection과 feature extraction의 차이는 original feature을 유지하느냐 아니냐.
• feature selection: sequential backward selection 같은 feature selection 알고리듬은 original feature을 유지함(original feature를 그대로 선택하기 때문에 상대적으로 해석하기 쉬움).
• feature extraction: 새로운 feature space로 data를 변형(이 때, 각 feature 간 상관관계를 고려)함.

feature extraction의 장점.

• improve storage space or computational efficiency
• reducing the curse of dimensionality
• feature간 상관관계를 고려한다는 장점이 있음.

Dimensionality reduction

Dimensionality reduction is the task of reducing the number of features in a dataset. In machine learning tasks like regression or classification, there are often too many variables to work with. These variables are also called features. The higher the number of features, the more difficult it is to model them, this is known as the curse of dimensionality.

https://neptune.ai/blog/dimensionality-reduction

하나의 data가 갖는 feature가 100개면, 그 data는 100차원 공간 안에 있는 data.

• 일반적으로 차원이 증가할수록 데이터 간의 거리가 증가(data가 위치할 수 있는 공간의 부피가 증가)하기에 data의 밀도가 희소한 구조를 갖게됨.
• feature가 많은면 다중 공선성 문제(Multicollinearity problem) 또한 발생할 수 있음.
• 다중 공선성 문제로 인해 서로 다른 feature들 간의 상관관계가 높은 경우, 한 feature의 변화가 다른 feature에 영향을 줌.

feature의 수가 너무 많아지면, 위와 같은 문제들로 인해 결과적으로 모델의 성능이 낮아짐.

• feature extraction은 이러한 문제를 해결하기 위해 100차원의 data를 100차원 보다 낮은 n차원으로 compression 하는 것.

본 chapter에서는 아래 3가지 dimensionality reduction 방법을 배움.

• Principal Component Analysis(PCA): unsupervised data compression.
  - unsupervised 기반이기 때문에 y값 없이, x값만을 활용한 방법.
• Linear Discriminant Analysis(LDA): supervised 방식의 dimensionality reduction techique for maximizing class separability
• Kernel Principal Component Analysis(KPCA)를 사용한 비선형 차원 축소.

1. Principal Component Analysis(PCA)

PCA: help us to identify patterns in data based on the correlation between features.

• PCA is linear transformation techniques.
• PCA는 고차원의 데이터를 저차원의 데이터로 환원시키는 기법.

PCA의 핵심은 data를 축에 사영(projection)했을 때, 각 data(data point)들의 분산이 최대로 보존되는 data의 축(Principal Component)을 찾아 그 축으로 차원을 축소하는 것.

• 분산이 최대로 유지되는 data의 축(Principal Component)을 찾는 이유는 compression으로 인한 정보의 손실을 최소화하기 위함.

2차원을 기준으로 PCA는 분산이 최대인 1번째 축을 찾고, 1번째 축에 직교하며 남은 분산이 최대인 2번째 축을 찾음.

PC를 찾기 위해서는 covariance matrix(공분산 행렬)의 eigen vector(고유 벡터) 값을 찾아야 함.

• 가장 큰 값이 우리가 원하는 PC에 만족한다고 볼 수 있음.

PCA는 기존 data vector를 선형 변환하여 사영함. 때문에 비선형 data 분포에는 적합하지 않음.

• SVM kernel trick과 유사한 kernel을 활용하여 비선형 변환을 수행하는 kernelized PCA가 있음.

https://seongyun-dev.tistory.com/4
https://angeloyeo.github.io/2019/07/27/PCA.html
https://www.youtube.com/watch?v=FhQm2Tc8Kic
https://excelsior-cjh.tistory.com/167

2. Kernel Principal Component Analysis(KPCA)

KPCA is an extension of principal component analysis (PCA) using techniques of kernel methods.

• PCA에 kernel trick을 적용한 것으로 선형 변환을 수행하는 PCA와 달리, KPCA는 비선형 변환을 수행.

Non-linear dimensionality reduction through the use of kernels.

• kernel function을 통해 data를 고차원으로 이동시킨 후, PCA를 적용.
• 대표적인 kernel function은 아래의 2개
  - Polynomial kernel function(다항커널함수)
  - RBF(radius basis function) kernel(be called Gaussian kernel) function이 있음.

https://www.youtube.com/watch?v=6Et6S03Me4o&list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW&index=15
https://garden-k.medium.com/%EB%85%BC%EB%AC%B8-kernel-principal-component-analysis-and-its-applications-in-face-recognition-and-active-shape-5b868e25fac4

3. Linear Discriminant Analysis(LDA)

LDA(Linear Discriminant Analysis)는 차원 축소의 개념으로 Topic modeling에 등장하는 LDA(Latent Dirichlet Allocation)와 다름.

LDA는 data를 특정 한 축에 사영(projection)한 후, 서로 다른 2개의 클래스를 잘 구분할 수 있는 직선(linear)을 찾는 것이 목표.

LDA는 클래스를 가장 잘 구분해주는 축(직선)을 찾기 위해 클래스 간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화하는 방식을 따름(SB / SW).

• 즉, 사영 후 두 클래스의 중심(평균)이 서로 멀도록, 그 분산이 작도록 하는 직선을 찾아야 함.
• SB = between-class scatter (클래스 간 분산); SW = within-class scatter (클래스 내 분산)

https://ratsgo.github.io/machine%20learning/2017/03/21/LDA/

PCA vs LDA

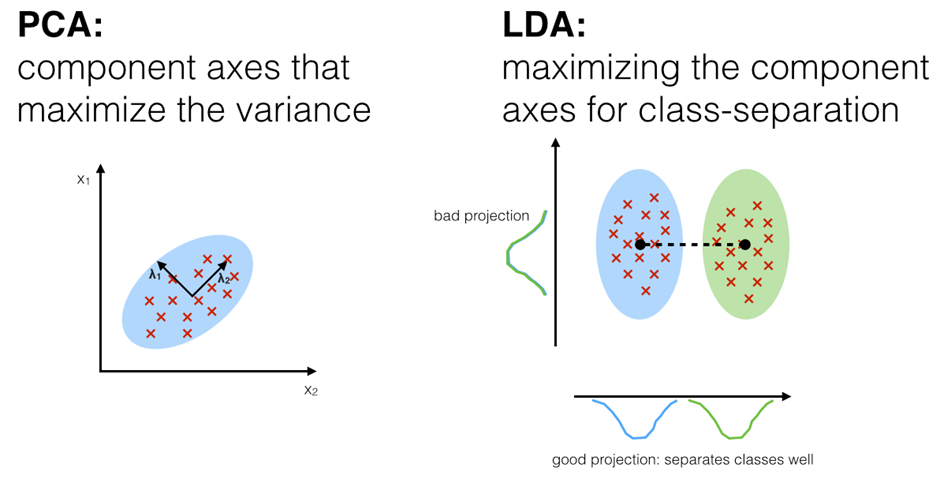
• Both Linear Discriminant Analysis (LDA) and Principal Component Analysis (PCA) are linear transformation techniques that are commonly used for dimensionality reduction.

PCA can be performed before LDA to regularize the problem and avoid over-fitting.
Both Need to first step, Standardize the d-dimensional dataset(standardizing the data)

• Data의 표준화(또는 정규화) 작업이 선행되는 이유: data를 구성하는 각각의 feature 마다 취할 수 있는 값의 범위가 다르므로, feature의 영향력을 동일 선상에서 비교하기 위함.

https://velog.io/@chiroya/23-PCA-LDA#pca-principal-component-analysis---%EC%A3%BC%EC%84%B1%EB%B6%84-%EB%B6%84%EC%84%9D
https://stats.stackexchange.com/questions/106121/does-it-make-sense-to-combine-pca-and-lda
https://sebastianraschka.com/Articles/2014_python_lda.html

4. t-Distributed Stochastic Neighbor Embedding (t-SNE)

• t-SNE는 비선형적인 방법의 차원 축소 방법

PCA +LDA.
PCA + t-SNE 활용.

PCA를 통해, feature extraction을 1차적으로 해준 후에 LDA(t-SNE)를 적용.