#23 PCA & LDA

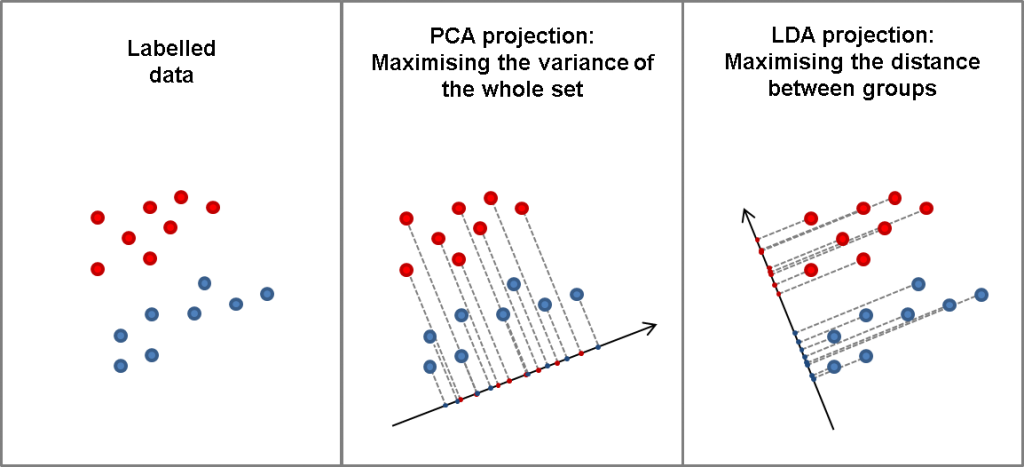
차원 축소 중, Feature Extraction 에는 PCA와 LDA라는 기법이 있다. 둘 다 같은 상위 분류에 속하기 때문에, 아래와 같은 특징을 갖고 있다.

Feature Extraction

1) 변수의 변환을 통해 새로운 변수 추출

2) 차원의 저주로 인한 과적합을 줄일 수 있다.

3) 규제가 없는 모델에서 주로 사용

3) 변수의 개수를 많이 줄일 수 있지만 추출된 변수의 해석이 어려움

PCA (Principal Component Analysis) - 주성분 분석

데이터의 피쳐들 간의 움직이는 정도인 공분산 행렬을 이용한 차원축소 방법.

• 비지도 학습

• 가장 대표적인 차원 축소 기법

• 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법

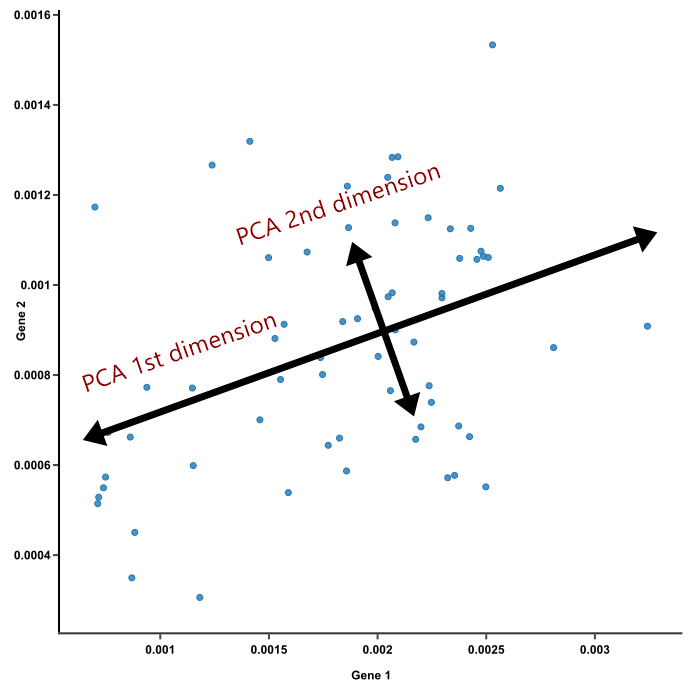
• 가장 큰 분산을 가지는 축을 기반으로 차원을 축소시키는 기법

목적

최소한의 loss를 가지고 정보를 압축하는 것.
→ 가장 높은 분산을 가지는 차원으로 축소를 수행하는 것.

핵심

데이터를 축에 사영했을 때 가장 높은 분산을 가지는 데이터의 축을 찾아 그 축으로 차원을 축소하는 것인데, 이 축을 주성분이라고 함.

※ 높은 분산을 가지는 축을 찾는 이유는 정보의 손실을 최소화하기 위함.

사영했을 때 분산이 크다
= 원래 데이터의 분포를 잘 설명할 수 있다
= 정보의 손실을 최소화 할 수 있다

independent variable들 사이에 correlation을 없애고, 숨은 latent variable을 찾아내거나, 노이즈(noise)를 줄일 때 사용.

데이터가 부실한 image classification에서 효과적

• 영상 인식
• 데이터 압축 (차원 감소)
• 노이즈 제거 등

방법

1. 모든 변수 $x$ 에 대해 임의의 기저 (basis) 또는 계수 ($x$ 개수)로 선형 결합 → 각 기저로 사영 변환 후의 변수

2. 정사영 (projection)을 통해 $n$차원 공간상의 데이터를 $k (k < n)$차원의 데이터셋으로 변환

3. 매니폴드 (manifold)실제 데이터셋이 차원이 낮은 매니폴드에 가깝게 놓여있다고 가정하고 문제를 해결

과정

① 입력 데이터 세트의 공분산 행렬을 구함.
② 공분산 행렬을 고유값 분해해서 고유벡터와 고유값을 구함.
③ 고유값이 가장 큰 순으로 K개 (변환 차수) 만큼 고유벡터를 추출.
④ 고유벡터에 입력 데이터를 선형 변환.

LDA (Linear discriminant analysis) - 선형 판별 분석

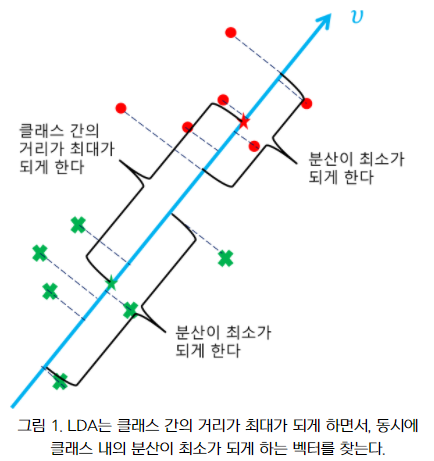
공분산 행렬이 아닌, 클래스 내부와 클래스 간 분산 행렬에 기반해 고유벡터를 구하고 입력 데이터를 투영하는 방식.

→ 클래스 분리를 최대화하는 축을 찾기 위해, 클래스 간 분산을 최대화하고, 클래스 내부 분산은 최대한 작게 가져가는 방식.

• 지도 학습 (차원 축소를 하며 label 정보를 가능한 많이 유지한다.)

• 클래스를 최적으로 구분할 수 있는 특성 부분 공간을 찾는다.

• PCA 보다 classification에서 뛰어나다. (SVM 같은 분류 알고리즘에 적절)

차원을 축소하는 데 있어 클래스 간의 차별성을 최대화할 수 있는 방향으로 수행.

과정

① 클래스 내부와 클래스 간 분산 행렬을 구함.
② 클래스 내부 분산 행렬의 역치 행렬과 클래스 간 분산 행렬의 곱을 분해하여 고유벡터와 고유값을 구함.
③ 고유값이 가장 큰 순으로 $K$개 추출.
④ 추출된 고유벡터를 이용해 입력 데이터를 선형 변환.

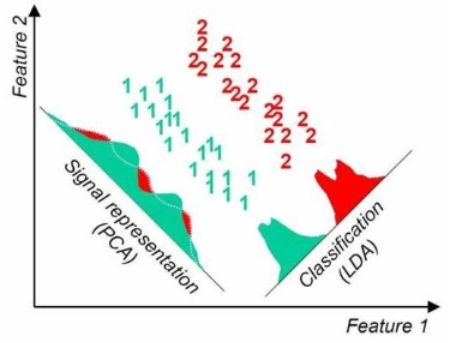
PCA vs LDA

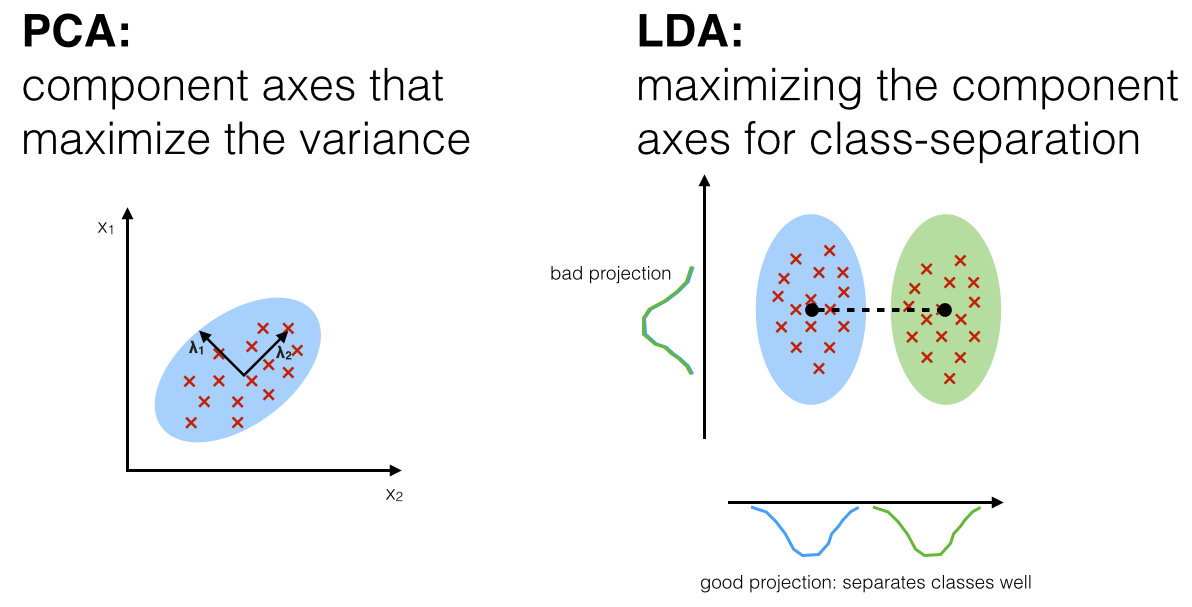
PCA : unsupervised learning
데이터의 클래스의 차이가 평균보다 분산의 차이에 있을 때, PCA는 LDA보다 뛰어난 성능을 보여준다.

LDA : supervised learning
데이터의 클래스의 차이가 분산보다 평균의 차이에 있을 때, LDA는 PCA보다 뛰어난 성능을 보여준다.

3D plot으로 데이터를 표현할 때, LDA는 PCA보다 뛰어난 성능을 보여준다.

PCA와 유사하게 입력 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법.

LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소.

PCA는 입력 데이터의 변동성(분산)이 가장 큰 축을 찾음,
→ 데이터가 넓게 분포(분산이 큼)되어 있도록 하는 새로운 축을 찾음.

LDA는 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾음.
→ 클래스들을 가장 잘 구분할 수 있는 새로운 축을 찾음.

ref ) https://blog.naver.com/PostView.naver?blogId=paragonyun&logNo=222465847517&from=search&redirect=Log&widgetTypeCall=true&directAccess=false

https://velog.io/@swan9405/PCA

https://kjwan4435.tistory.com/85

https://sjpyo.tistory.com/44