딥러닝 용어정리 (1) - L1 Regularization, L2 Regularization

Wooseok Jung·2023년 5월 16일

CS면접대비 DeepLearning

DeepLearning

목록 보기

1/2

How to Prevent Overfitting

딥러닝을 이용한 모델 학습의 가장 큰 관건은, 주어진 데이터셋을 가지고 특정 테스크에 일반화되어 잘 학습된 모델을 만드는 것이다.

따라서 Overfitting 문제를 해결하는 것이 무척 중요하며, 이에는 다양한 방법들이 사용된다. 대표적으로 다음과 같다.

데이터의 수를 늘린다
모델의 Complexity를 줄인다
Regularization을 사용한다.

1,2 번 방법에 대해서도 차차 이야기하겠지만 오늘은 L1-Regularization과 L2-Regularization에 대하여 이야기하겠다.

Regularization

우선 데이터셋의 bias를 제거하고 증대하고, 모델의 Complexity를 줄여도 Overfitting 문제가 해결이 되지 않는다면, Regularization을 적용해야한다.

Regularization은 모델의 복잡도를 낮추기 위한 방법이다. Weight 값이 너무 크면 지나치게 구불구불한 형태의 계산함수가 만들어지는데, Regularization은 Weight가 너무 큰 값을 가지지 않게 방지한다.

Regularization에 대해서 이야기 하기 전에 Norm과 L1 Norm, L2 Norm의 차이, 그리고 Loss들과 차이에 대해서 알아보자.

1. Norm

\left\| x\right\|_{p} := \begin{pmatrix} \sum_{n}^{i=1}\left|x_{i}\right|^{p}\end{pmatrix}^{\frac{1}{p}}

Norm은 벡터의 크기(길이) 를 측정하는 방법이다. 선형대수학에서 자주 접할 수 있는데, 벡터가 얼마나 큰지 (차원의 크기가 아닌 구성 요소의 Magnitude) 알려주는 것이라고 생각하면 간단하다. 혹은 두 벡터사이의 거리를 측정하는 방법이기도 하다.

p 는 Norm의 차수를 의미한다. p=1이면 L1 Norm이고, p=2 이면 L2 Norm 이다.
n은 해당 벡터의 원소의 개수를 의미한다.

2. L1 Norm

d_{1}\left ( p, q \right )= \left\|p - q\right\|_{1} = \sum_{n}^{i=1}\left|p_{i}-q_{i} \right|

위와 같이 p,q라는 벡터가 있을 때, 두 벡터 차의 절댓값의 합이 바로 L1 Norm이다.

3. L2 Norm

\left\| x \right\|_{2} = \sqrt{\sum_{n}^{i=1}\left|x_{i}\right|^{2}}

L2 Norm은 n차원 좌표평면 (유클리드 공간)에서 피타고라스 정리를 이용한 벡터간의 유클리디안 거리 (직선거리)를 나타낸다. 여기서 한 벡터가 원점이면 X의 원점간 직선거리라고 볼수 있다.

4. L1 Norm, L2 Norm 차이

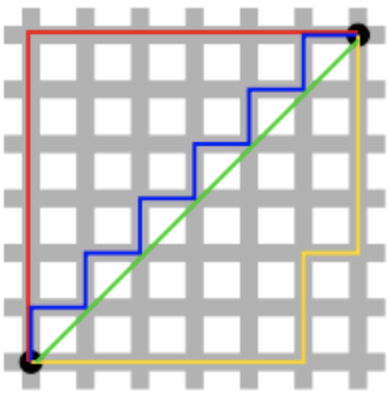
검정색 두 점 사이의 L1 Norm 은 빨강, 파랑, 노랑색 선으로 표현될 수 있지만, L2 Norm은 오직 초록색(대각선) 선으로만 표현될 수 있다. L1 Norm은 여러가지 path를 가지지만, L2 Norm은 Unique Shortest Path를 가진다.

5. L1 Loss, L2 Loss

L_{1} = \sum_{n}^{i=1}\left|y_{i}-f(x_i)\right|

L_{2} = \sum_{n}^{i=1}\left ( y_i -f(x_i) \right )^{2}

$y_i$ 는 실제값, $f(x_i)$ 는 예측값을 의미한다.

L1 Loss : 실제값과 예측값 사이의 오차 절대값의 합을 L1 Loss라고 한다.
L2 Loss : 오차의 제곱합

Robustness

L2 loss는 outlier의 정도가 심하면 심할수록 직관적으로 제곱을 하기에 계산된 값이 L1보다는 더 큰 수치로 작용하기때문에 Robustness가 L1보다 적게된다.

따라서 Outlier가 효과적으로 적당히 무시되길 원한다면, 비교적 이상치의 영향력을 덜 받는 L1 loss를 선택하고, 반대로 이상치의 등장이 중요한 상황이면 L2 loss를 취해야한다.

6. Regularization

모델 복잡도에 대한 패널티로 정규화는 과적합을 예방하고 Generalization 성능을 높이는데 도움을 준다. RegularizationDpsms L1/L2 Regularization, Dropout, Early Stopping등이 존재한다.

Regulariztion은 특정 가중치가 너무 과도하게 커져 과적합이 되는 것을 방지한다.

L1 Regularization (Lasso)

Cost = \frac{1}{n}\sum_{n}^{i=1}\left\{L(y_i, \hat{y_i}) + \frac{\lambda }{2}|w| \right\}

L1 Regularization은 기존 Cost Functiond에 가중치 (W)의 크기가 포함되면서, 학습의 방향이 Cost Function 뿐만이 아니라 가중치 또한 줄여나가는 방식으로 진행이 된다. 람다 $\lambda$ 는 학습률 하이퍼 파라미터로, 0에 가까워질 수록 정규화의 효과는 없어진다.

L1 Regularization이 적용된 Cost Function을 편미분한 결과로

w \to w - \frac{\eta \lambda}{n}sgn(w) - \eta \frac{\partial C0}{\partial w}

$sgn(w)$ 는 실수의 부호를 출력하는 함수이므로, w의 크기에 상관없이 w 부호에 따라 상수값을 빼주는 방식으로 진행된다.

L2 Regularization (Ridge)

Cost = \frac{1}{n}\sum_{n}^{i=1}\left\{L(y_i, \hat{y_i}) + \frac{\lambda }{2}|w|^2 \right\}

기존의 Cost Function에 가중치의 제곱을 더함으로써, 가중치가 너무 크지 않은 방향으로 학습되게 된다.

위의 Cost Function을 편미분하게 되면,

w \to w - \eta \frac{\partial C0}{\partial w} - \frac{\eta \lambda}{n}

이는 곧 w 에 $(1-\frac{\eta \lambda}{n})$ 을 곱함으로써 w 값이 감소되는 방향으로 진행되며, Weight Decay 라고도 불린다.

7. Regularization의 선택기준

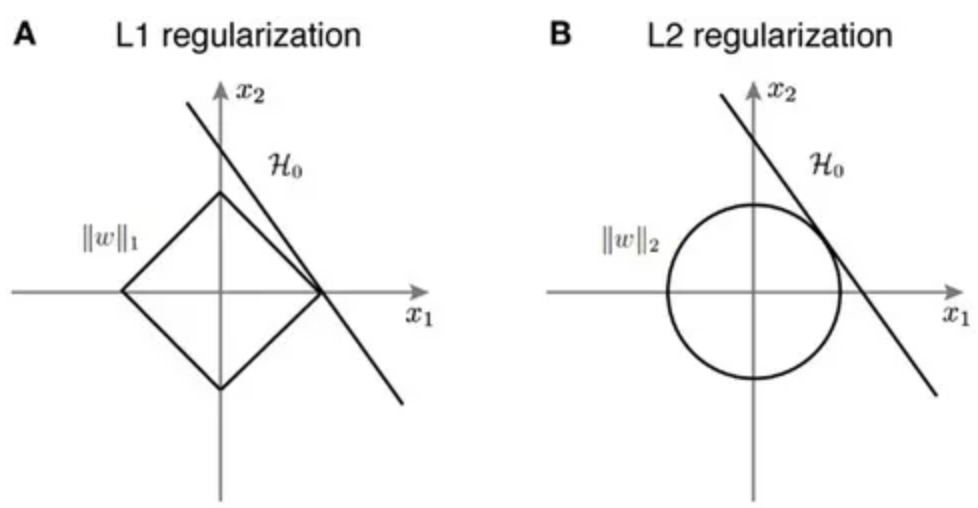
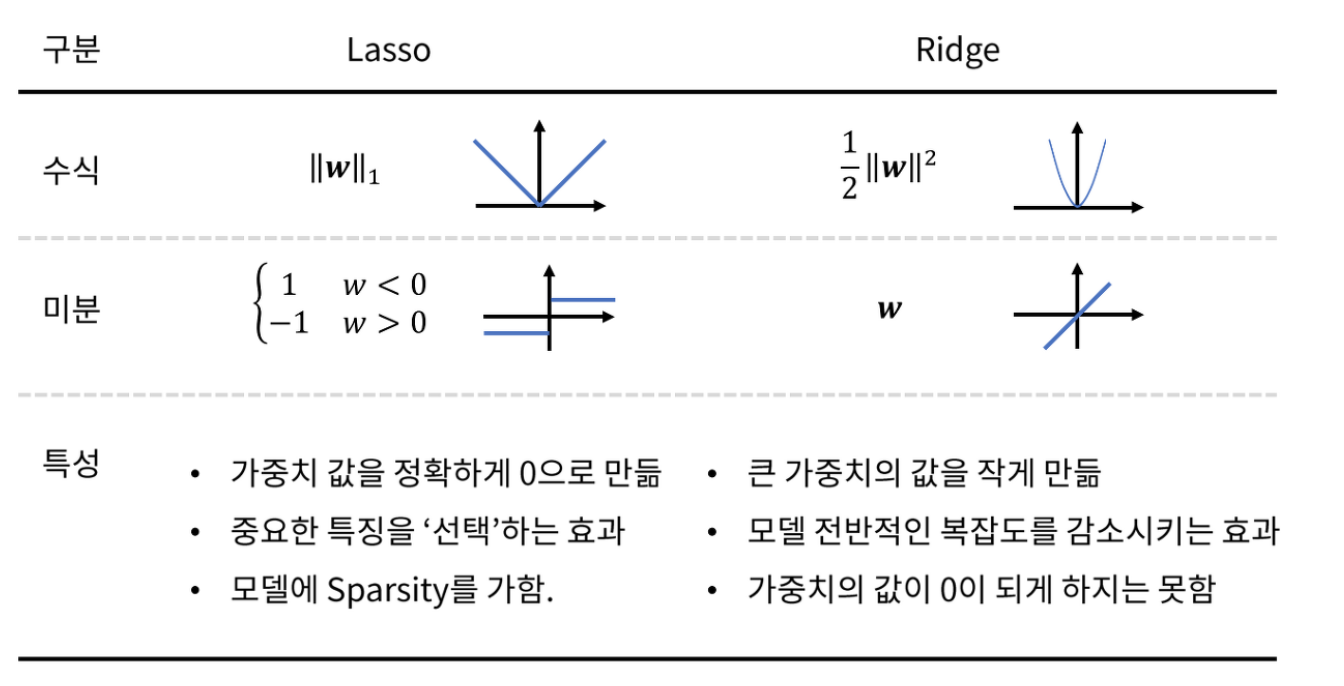
Regularization의 의미인 가중치 w를 감소시키는 방향으로 학습시킨다는 것은 결국 Local Noise에 Robust한 모델을 만들겠다는 의미이다. 따라서 Outlier에 Robust해지고 일반화된 모델이 만들어지는 것을 목표로 하는것이다.

L1 Regularization

가중치 업데이트 시, 가중치의 크기에 상관없이 상수값을 빼면서 진행된다.
L1 Norm에서 봤듯이, L1 은 Feature Selection이 가능하다. 이는 곧 L1 Regularizaiton의 특징이 되기도 한다.
가중치들은 0으로 수렴하는 경향이 있으며, 중요한 가중치들만 남게 된다.
의미있는 값을 강조하고 싶은 Sparse Model에 적합하다.
즉, 변수선택이 가능하다.

L2 Regularization