TIL_44 : 행렬과 벡터

🙄 행렬과 벡터

---

➡ 행렬 (Matrix)

• 수를 직사각형의 형태로 나열한 것

$A$ = $\begin{bmatrix}1&1&0&2\\2&1&4&1\\ \end{bmatrix}$

• $A$의 경우 행이 2개 열이 4개 있는데, 이걸 2x4 행렬 혹은 "행렬의 차원이 2x4다" 라고 함
• $A_{ij}$는 행렬 $A$의 $i$행 $j$열에 있는 원소를 뜻함
• $A_{21}$은 $A$의 2행 1열에 있는 원소 2를 나타냄

➡ 벡터

• 일종의 행렬, 행이 하나밖에 없거나 열이 하나밖에 없는 행렬

$a$ = $\begin{bmatrix}1\\0\\2\\4\\1 \end{bmatrix}$

$b$ = $\begin{bmatrix}1&0&2&4\\ \end{bmatrix}$

• $a$ 같은 경우 열이 하나만 있기 때문에 열 벡터
• $b$는 행이 하나만 있기 때문에 행 벡터

👉 열 벡터를 사용하는 경우가 더 많기 때문에, 그냥 벡터라고 하면 열 벡터를 뜻함

• 벡터는 무조건 열이 하나밖에 없거나 행이 하나밖에 없기 때문에 백터의 차원을 이야기 할 때는
  원소의 개수를 얘기함
  ex) $a$는 5차원 열 벡터, $b$는 4차원의 행 벡터

👉 벡터가 아닌 일반 행렬은 주로 대문자 알파벳으로, 벡터는 주로 소문자 알파벳으로 나타낸다

🙄 numpy로 행렬 사용하기

---

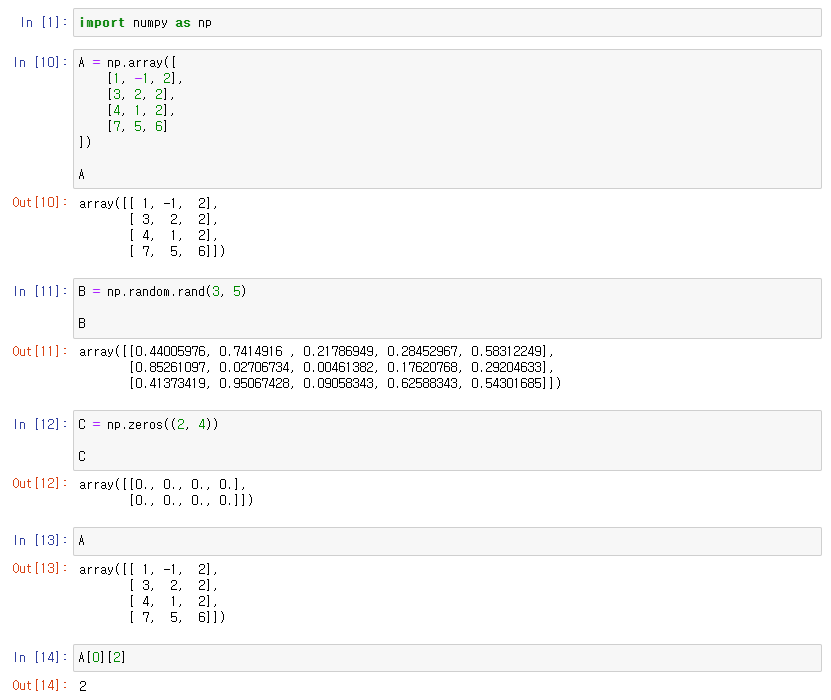
• A : 일반 행렬 생성
• B : 0부터 1까지의 랜덤한 수로 행렬 생성, 파라미터 (행의 수, 열의 수)
• C : 0으로 채워진 행렬 생성, 파라미터 ((행의 수, 열의 수)) 📌 괄호를 한번 더 쓰자

🙄 행렬 연산_1 (덧셈, 스칼라곱)

---

➡ 행렬 덧셈

• 같은 위치에 있는 원소들끼리 더해주면 됨

$A$ = $\begin{bmatrix}1&1\\2&3\\ \end{bmatrix}$, $B$ = $\begin{bmatrix}3&1\\2&4\\ \end{bmatrix}$

$A+B$ = $\begin{bmatrix}1&1\\2&3\\ \end{bmatrix}$ + $\begin{bmatrix}3&1\\2&4\\ \end{bmatrix}$ = $\begin{bmatrix}4&2\\4&7\\ \end{bmatrix}$

👉 행렬을 더하기 위해서는 두 행렬의 차원이 같아야 함 = 행 수와 열 수가 같아야 함

➡ 스칼라곱

• 행렬과 수를 곱하는 것을 스칼라곱이라고 함
• 스칼라 : 행렬의 원소가 아닌 일반 수
  ex) 아래 $i$

$i = 5$, $A$ = $\begin{bmatrix}3&1\\2&3\\ \end{bmatrix}$

$iA$ = $\begin{bmatrix}15&5\\10&15\\ \end{bmatrix}$

🙄 행렬 연산_2 (두 행렬의 곱)

---

➡ 두 행렬의 곱

$A$ = $\begin{bmatrix}1&3&1\\2&2&1\\ \end{bmatrix}$, $B$ = $\begin{bmatrix}5&6\\4&2\\3&1\\ \end{bmatrix}$

• $A$는 2 by 3 행렬이고, $B$는 3 by 2 행렬

$AB$ = $\begin{bmatrix}20&13\\21&17\\ \end{bmatrix}$

• 1행 1열에는 $A$의 1행과 $B$의 1열을 곱한 결과가 들어감
  $1*5 + 3*4 + 1*3 = 20$

➡ 행렬 차원

$AB$ = $\begin{bmatrix}20&13\\21&17\\ \end{bmatrix}$

• $A$와 $B$를 곱하면, $A$가 행을 제공하고 $B$가 열을 제공
• 결과 행렬의 행 수는 $A$의 행 수랑 똑같고, 열 수는 $B$의 열 수랑 똑같음

• $m*n$인 행렬 $A$와 $n*p$인 행렬 $B$
• $A$의 열 수와 $B$의 행 수가 같아 두 행렬을 곱할 수 있음
• 곱하면 $A$의 행 수와 $B$의 열 수를 따서 $m*p$ 행렬이 결과로 나옴

👉 $A$의 열 수와 $B$의 행 수가 똑같아야 두 행렬을 곱할 수 있음

➡ 교환 법칙

• $3*4$ = $4*3$은 성립하지만 행렬에서 $A*B$ = $B*A$ 는 성립하지 않는다
• 계산조차 할 수 없는 경우가 대부분

계산 가능

$AB$ = $\begin{bmatrix}1&3&1\\2&2&1\\ \end{bmatrix} * \begin{bmatrix}5&6&1&4\\4&2&3&3\\3&1&-1&1\\ \end{bmatrix}$

계산 불가능

$BA$ = $\begin{bmatrix}5&6&1&4\\4&2&3&3\\3&1&-1&1\\ \end{bmatrix} * \begin{bmatrix}1&3&1\\2&2&1\\ \end{bmatrix}$

➡ 요소별 곱하기

• 행렬 덧셈 연산과 똑같은 성질을 갖는 연산
• $A$Ο$B$로 표현

$A$ = $\begin{bmatrix}1&2\\3&4\\ \end{bmatrix}$, $B$ = $\begin{bmatrix}-1&2\\3&1\\ \end{bmatrix}$

$A$Ο$B$ = $\begin{bmatrix}-1&4\\9&4\\ \end{bmatrix}$

🙄 numpy로 행렬 연산하기

---

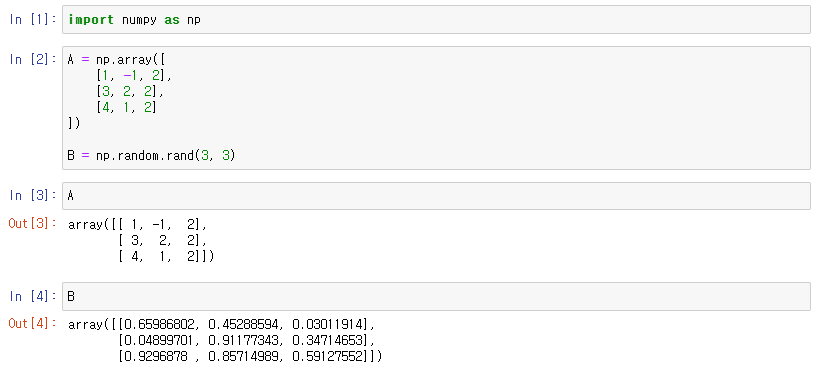
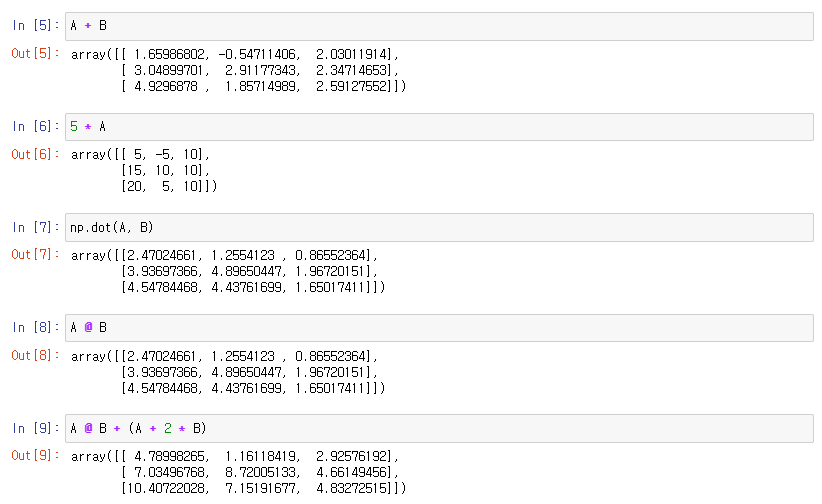
두 행렬 곱셈 방법

• np.dot(A, B)
• A @ B

🙄 특수 행렬

---

➡ 전치 행렬 (transposed matrix)

• 행렬 전환된 행렬
• 행렬 계산할 때 모양을 맞춰야 할 때가 존재, 기존 행렬에서 모양이 안 맞으면 전치 행렬을 사용

$A$ = $\begin{bmatrix}1&2&1\\3&2&2\\ \end{bmatrix}$

$A^T$ = $\begin{bmatrix}1&3\\2&2\\1&2\\ \end{bmatrix}$

➡ 단위 행렬 (identity matrix)

• 왼쪽 위에서부터 대각선으로는 원소가 1, 그 외에는 모두 0인 행렬
• 단위 행렬은 항상 정사각형의 모양
• 단위 행렬의 목적 : 어떤 행렬이든 간에 단위 행렬을 곱하면 기존 행렬이 유지
• 자연수 1 역할

$A$ = $\begin{bmatrix}3&4\\1&2\\ \end{bmatrix}$, $I$ = $\begin{bmatrix}1&0\\0&1\\ \end{bmatrix}$

$AI$ = $\begin{bmatrix}3&4\\1&2\\ \end{bmatrix}$

➡ 역행렬 (inverse matrix)

• 곱해서 단위 행렬이 나오는 행렬
• 자연수 역수 역할

$A$ = $\begin{bmatrix}3&4\\1&2\\ \end{bmatrix}$, $A^{-1}$ = $\begin{bmatrix}1&-2\\-\frac{1}{2}&\frac{3}{2}\\ \end{bmatrix}$

$A * A^{-1}$ = $\begin{bmatrix}1&0\\0&1\\ \end{bmatrix}$

👉 모든 행렬에 역행렬이 있는 건 아님

🙄 numpy로 전치, 단위, 역행렬 사용하기

---

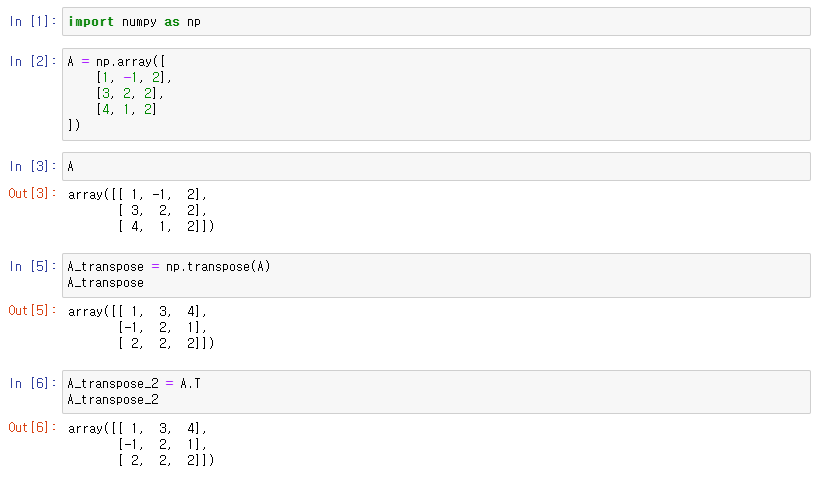
행렬 A의 전치 행렬 만들기

• np.transpose(A)
• A.T

단위 행렬 만들기

• np.identity()

행렬 A의 역행렬 만들기

• np.linalg.pinv(A)