TIL_48 : 로지스틱 회귀

🙄 로지스틱 회귀

---

➡ 로지스틱 회귀 (Logistic Regression)

• 데이터에 가장 잘 맞는 시그모이드 함수를 찾는 것

➡ 시그모이드 함수

• $S(x)=\frac{1}{1+e^{-x}}$

• 무조건 0과 1 사이의 결과를 냄
• $e$는 2.718이라는 양수

• $S(\infty)=\frac{1}{1+e^{-\infty}}=\frac{1}{1+0}=1$
• $S(-\infty)=\frac{1}{1+e^{\infty}}=\frac{1}{1+\infty}=0$

• $x$가 엄청나게 작으면 0에 가까워지고, $x$가 엄청나게 크면 1에 가까워짐
• 일차 함수는 결과가 얼마든지 작아질 수 있고 커질 수 있기 때문에 분류에 부적합
• 선형 회귀는 예외적인 데이터 하나에 가설 함수가 민감하게 반응
• 시그모이드 함수는 예외적인 데이터에 크게 영향을 받지 않음
• 0과 1 사이의 연속적인 값이기 때문에 로지스틱 분류가 아닌 로지스틱 회귀
• 주로 함수의 결괏값이 0.5보다 큰지 작은지 보고 분류

🙄 가설 함수

---

➡ 가설 함수

• 특정 데이터에 대해서 입력 변수를 받으면 목표 변수를 예측해 주는 함수
• 선형 회귀에서 썼던 아래의 가설 함수를 발전시키면 로지스틱 회귀의 가설 함수가 됨
• 로지스틱 회귀 가설 함수를 $h$로 표현하기 위해 $g$로 표현

$\theta$ = $\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\\.\\.\\\theta_n \end{bmatrix}$

$x$ = $\begin{bmatrix}1\\x_1\\x_2\\.\\.\\x_n \end{bmatrix}$

$g_\theta(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+...\theta_nx_n$
$g_\theta(x)=\theta^Tx$

$h_\theta(x)=\frac{1}{1+e^{-g_\theta(x)}}$
$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$

• 선형 회귀에서 썼던 가설 함수 $g$의 아웃풋을 시그모이드 함수의 인풋으로 사용
• 아웃풋은 0과 1 사이의 어떤 수

🙄 손실 함수

---

➡ 로그 손실 (log-loss, cross entropy)

• 손실의 정도를 로그 함수로 결정하기 때문에 로그 손실
• 데이터에 잘 맞는 가설 함수를 찾기 위해 손실 함수를 이용해서 가설 함수를 평가
  $logloss(h_\theta(x), y) = \begin{cases} -\log(h_\theta(x)) & \text{y=1} \\ -\log(1-h_\theta(x)) & \text{y=0} \end{cases}$

• 한 줄로 표현하면 아래와 같다
  $logloss(h_\theta(x),y)=-y\log(h_\theta(x))-(1-y)\log(1-h_\theta(x))$

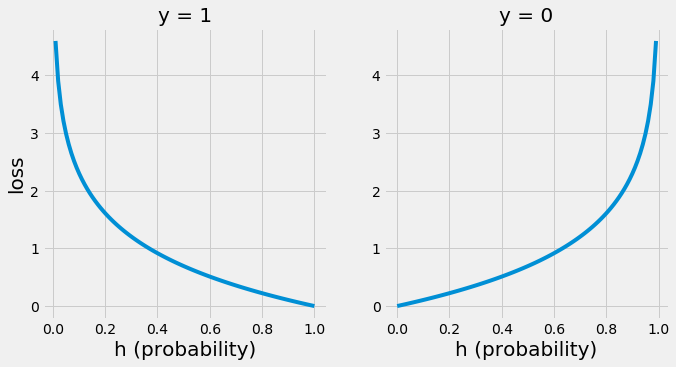
• 로그 손실은 실제 아웃풋 $y$가 1인 경우와 0인 경우로 나눠서 계산

• $y$가 1인 경우, 예측 값이 1에 가까울수록 손실이 0에 가깝고 멀어질수록 가파르게 커짐

• $y$가 0인 경우에는 정반대

➡ 로그 손실 함수

• 목표는 각 데이터에 대해서 손실을 구한 후, 손실의 평균을 내는 것

• $J(\theta)=\frac{1}{m}\sum_{i=1}^m[(logloss(h_\theta(x),y))]$

• $J(\theta)=\frac{1}{m}\sum_{i=1}^m[-y^{(i)}\log(h_\theta(x^{(i)}))-(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$

• $\theta$ 값들을 어떻게 설정하느냐에 따라 손실이 달라지므로 손실 함수의 인풋은 $\theta$

🙄 경사 하강법

---

➡ 경사 하강법

• 가설 함수와 손실 함수는 다르지만, 경사 하강법을 하는 방법은 선형 회귀랑 동일
• $\theta$ 값들을 모두 0으로 지정하거나 모두 랜덤하게 지정

• $\theta_0$, $\theta_1$, $\theta_2$ 3개가 있다고 가정한다면
  $\theta_0=\theta_0-\alpha\frac{\partial}{\partial\theta_0}J(\theta)$
  $\theta_1=\theta_1-\alpha\frac{\partial}{\partial\theta_1}J(\theta)$
  $\theta_2=\theta_2-\alpha\frac{\partial}{\partial\theta_2}J(\theta)$

• 손실 함수를 편미분하고, 그 결과에 학습률 알파를 곱한 뒤 기존 $\theta$에서 뺀다
• 모든 $\theta$를 업데이트하면 경사 하강을 한 번 했다고 할 수 있음
• 차이점은 손실 함수 $J$가 다르다는 것
• 하지만 편미분을 하면 선형 회귀랑 똑같은 식이 나옴
  $\theta_j=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})*x_j^{(i)}$

• 선형 회귀랑 거의 똑같지만 유일하게 다른 건 가설 함수 $h$
• 선형 회귀 가설 함수는 일차 함수지만 로지스틱 회귀 가설 함수는 시그모이드 함수
• $h$에 시그모이드 함수를 대입해 각 $\theta$ 값을 업데이트

➡ 경사 하강법 간단하게 표현하기

• $\theta=\theta-\alpha\frac{1}{m}(X^T*error)$

➡ 경사 하강법 구현하기

import numpy as np

def sigmoid(x):
    """시그모이드 함수"""
    return 1 / (1 + np.exp(-x))
    
    
def prediction(X, theta):
    """로지스틱 회귀 가정 함수"""
    return sigmoid(X @ theta)
    

def gradient_descent(X, theta, y, iterations, alpha):
    """로지스틱 회귀 경사 하강 알고리즘"""
    m = len(X) 
    
    for _ in range(iterations):
        error = prediction(X, theta) - y
        theta = theta - alpha / m * X.T @ error 
    return theta
    
    
# 입력 변수
hours_studied = np.array([0.2, 0.3, 0.7, 1, 1.3, 1.8, 2, 2.1, 2.2, 3, 4, 4.2, 4, 4.7, 5.0, 5.9])  # 공부 시간 (단위: 100시간)
gpa_rank = np.array([0.9, 0.95, 0.8, 0.82, 0.7, 0.6, 0.55, 0.67, 0.4, 0.3, 0.2, 0.2, 0.15, 0.18, 0.15, 0.05]) # 학년 내신 (백분률)
number_of_tries = np.array([1, 2, 2, 2, 4, 2, 2, 2, 3, 3, 3, 3, 2, 4, 1, 2])  # 시험 응시 횟수

# 목표 변수
passed = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])  # 시험 통과 여부 (0: 탈락, 1:통과)

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    hours_studied,
    gpa_rank,
    number_of_tries
]).T

# 입력 변수 y 정의
y = passed

theta = [0, 0, 0, 0]  # 파라미터 초기값 설정
theta = gradient_descent(X, theta, y, 300, 0.1)  # 경사 하강법을 사용해서 최적의 파라미터를 찾는다
theta


# array([-1.35280508,  1.61640725, -1.83666046, -0.60286277])

🙄 정규 방정식

---

➡ 정규 방정식

• 선형 회귀는 손실 함수 $J (MSE)$가 convex (아래로 볼록) 할 뿐만 아니라, 편미분 원소들을 모두 선형식으로 나타낼 수 있기 때문에 정규 방정식 처럼 단순 행렬 연산만으로도 최적의 $\theta$ 값들을 구할 수 있음

• 로지스틱 회귀에서도 손실 함수 $J$ (로그 손실)가 아래로 볼록해 경사 하강법을 사용하면 항상 최적의 $\theta$ 값들을 구할 수 있음
• 하지만 $J$에 대한 편미분 원소들이 선형식이 아님, $\theta$가 $e$의 지수에 포함되어 있는데 지수로 포함된 식은 일차식으로만 표현하기가 불가능해 단순 행렬 연산만으로 최소 지점을 찾아낼 수 없음

🙄 scikit-learn으로 로지스틱 회귀

---

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

import pandas as pd  

wine_data = datasets.load_wine()
""" 데이터 셋을 살펴보는 코드
print(wine_data.DESCR)
"""

# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)

# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(wine_data.target, columns=['Y/N'])

# 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)

# 경고 메시지가 나오지 않게 학습시키기 전 아래 코드 한 줄 추가하기
y_train = y_train.values.ravel()

logistic_model = LogisticRegression(solver = 'saga', max_iter = 7500)

# 모델 학습
logistic_model.fit(X_train, y_train)

# y값 예측
y_test_predict = logistic_model.predict(X_test)

# 테스트 코드
score = logistic_model.score(X_test, y_test)
y_test_predict, score


# (array([0, 1, 0, 0, 2, 2, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0,
#        1, 1, 1, 0, 1, 2, 0, 1, 1, 0, 0, 0, 2]), 0.72222222222222221)