
🙄 결정 트리
➡ 결정 트리란?
예/아니오로 답할 수 있는 질문들이 있고, 그 질문들의 답을 따라가면서
데이터를 분류하는 알고리즘
leaf 노드는 항상 특정 예측값을 갖고 있고
나머지 노드들은예/아니오로 답할 수 있는 질문을 갖고 있다
if-else 구문을 이용한 간단한 결정 트리
def survival_classifier(seat_belt, highway, speed, age):
if not seat_belt:
if highway:
if speed > 100:
if age > 50:
return 1
return 0
print(survival_classifier(False, True, 110, 55))
print(survival_classifier(True, False, 40, 70))
print(survival_classifier(False, True, 80, 25))
print(survival_classifier(False, True, 120, 60))
print(survival_classifier(True, False, 30, 20))
# 0: 생존 예측, 1: 사망 예측
# 1
# 0
# 0
# 1
# 0➡ 지니 불순도 (gini impurity)
- 데이터 셋의 데이터들이 얼마나 섞여있는지를 나타냄
- 작을수록 데이터 셋이 순수하고, 클수록 데이터 셋이 불순
- 결정 트리의 목적은 학습 데이터를 직접 분류해보면서, 데이터들을 가장 잘 분류할 수 있는
노드들을 찾아내는 것
- 위 if문과 같이 정해져 있는 질문이 아닌, 경험을 통해 직접 질문을 정하는 것
- 손실 함수와 같이 질문을 평가하는 기준이 필요, 바로 지니 불순도
예시 : 독감 데이터
- 지니 불순도는 데이터 셋이 얼마나 불순한지를 숫자로 표현 공식은 다음과 같음
- 100개의 데이터, 70개가 독감, 30개가 일반 감기라면 지니 불순도는
- 100개의 데이터, 100개가 독감, 0개가 일반 감기라면 지니 불순도는
- 반대의 경우도 마찬가지
🙄 노드 평가하기
➡ 분류 노드 평가하기
- 고열, 기침, 몸살을 속성으로 갖는 데이터 셋으로 독감을 예측하는 결정 트리
- 가장 먼저
root node를 만들어야 하는데 방법은 두 가지
-
질문 노드를 만들지 않고 바로 분류 노드를 만든다
ex) 모든 데이터는 독감이다, 모든 데이터는 일반 감기이다 -
속성들을 이용해 질문 노드를 만든다
ex) 고열이 있나요?, 기침이 있나요?, 몸살이 있나요?
- 좋은 분류 노드는 최대한 많은 학습 데이터 예측을 맞춘다
- 데이터 셋이 순수할수록, 지니 불순도가 낮을수록 좋다
➡ 질문 노드 평가하기
- 결정 트리에서 좋은 질문은 데이터를 잘 나누는 질문
- 좋은 질문은 데이터를 잘 나눠서 아래 노드들이 분류하기 쉽게 만들어준다
- 질문으로 나뉜 데이터 셋이 순수할수록, 지니 불순도가 낮을수록 더 좋다
예시 : 고열로 나뉜 데이터 셋 불순도
| 고열 | 고열 X | |
|---|---|---|
| 독감 | 40 | 10 |
| 일반 감기 | 10 | 30 |
- 고열이 있는 데이터 셋 불순도
- 고열이 없는 데이터 셋 불순도
- 불순도 평균 내기
그냥 합치지 않고 각 데이터에 크기만큼 무게를 준다
➡ 노드 고르기
- 나머지 질문들의 불순도 계산 후 가장 작은 불순도를 가진 질문을
root node로 사용 - 나머지 노드들을 고르는 것도 똑같은 방식
- 가장 불순도가 낮은 노드를 골라주면 된다
- 트리가 몇 층까지 내려가는지를 트리의 깊이라고 표현
- 최대 깊이를 정해줄 수도 있는데 특정 깊이까지 내려오면
더 이상 불순도를 비교하는 게 아니라 분류 노드로 만들면 된다
➡ 속성이 숫자형일 때 질문 노드
- 데이터가 체온처럼 숫자형으로 있는 경우 만들 수 있는 질문이 엄청 많음
ex) 37.1도를 넘나요?, 37.4도를 넘나요?, 37.8도를 넘나요?
- 수많은 질문들 중, 하나를 고르는 방법
1. 데이터를 정렬
2. 각 연속된 체온 데이터의 평균을 계산
3. 평균들을 이용해 질문들을 하나씩 만들어 지니 불순도를 계산
4. 가장 낮은 지니 불순도를 갖는 수치를 사용
➡ 속성 중요도 (Feature Importance)
노드 중요도 (Node Importance)
- 한 노드에서 데이터를 두 개로 나눴을 때, 데이터 수에 비례해서
불순도가 얼마나 줄어들었는지를 계산하는 것
- 나눠지는 데이터 셋들에 대해서 점점 더 알아간다, 더 많은 정보를 얻는다라고 해서
이 수치를 정보증가량,information gain이라고도 함
root node의 중요도 계산
| root node | left node | right node | |
|---|---|---|---|
| 데이터 수 | 90 | 60 | 30 |
| 불순도 | 0.333 | 0.270 | 0.222 |
-
이렇게 모든 질문 노드의 중요도를 다 계산해 준다
-
고열 변수 중요도 =
- 모든 노드가 데이터를 양 갈래로 나누면서 나누는 데이터 셋들의 지니 불순도를 낮춤
- 전체적으로 낮춰진 불순도에서, 특정 속성 하나가 낮춘 불순도를 계산하는 것
- 이렇게 최종적으로 구한 값을 속성의 평균 지니 감소,
Mean Gini decrease라고 부르기도 함 - 특정 속성이 결정 트리 안에서 평균적으로 얼마나 불순도를 낮췄는지 계산할 수 있고,
결정 트리 안에서 그 속성이 얼마나 중요한지 판단할 수 있음
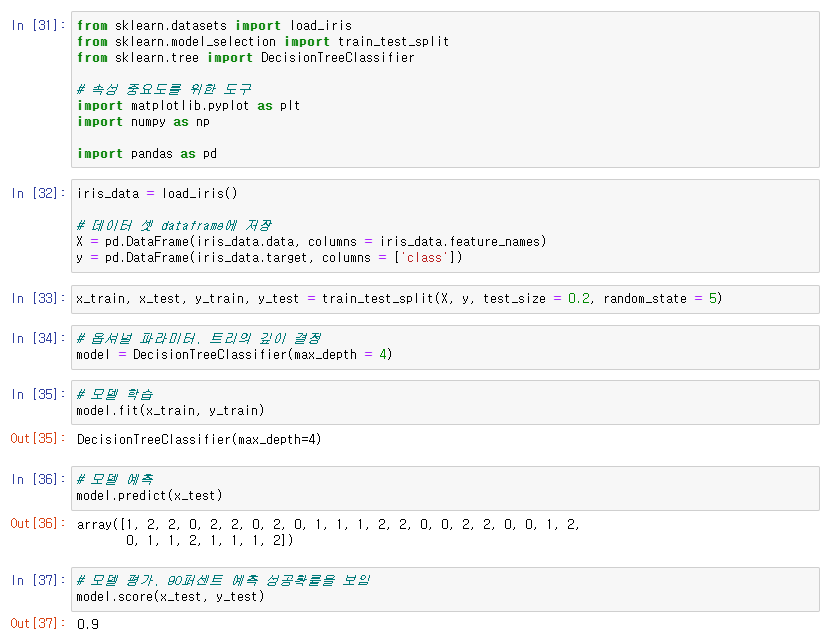
🙄 scikit-learn으로 결정 트리 사용
➡ 결정 트리
➡ 속성 중요도 확인
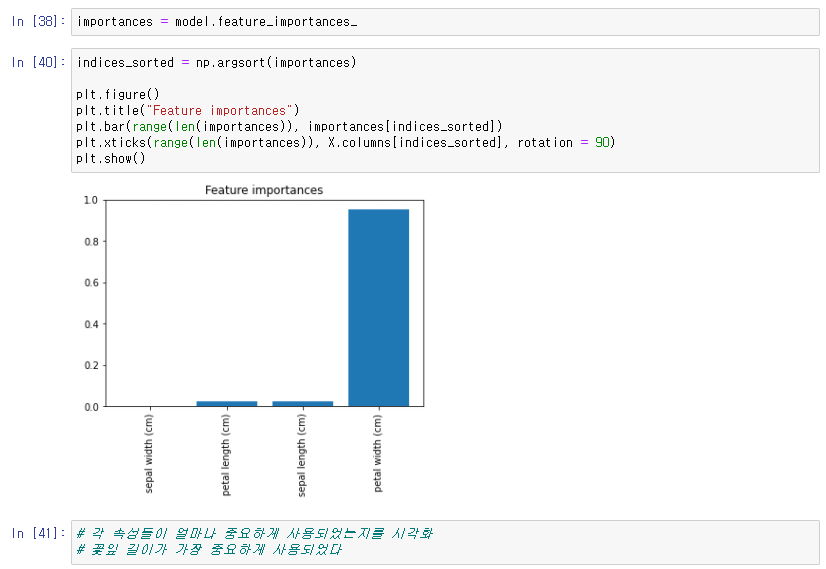
.png)