참조
https://velog.io/@gkdis6/알고리즘-강한-연결-요소-추출-알고리즘-Strongly-Connected-Component
https://mobuk.tistory.com/120
https://velog.io/@namsh1125/%ED%83%80%EC%9E%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
- DFS 1번을 기반으로 SCC를 찾는 알고리즘
- O(V+E)의 시간복잡도를 가짐
- 코사라주 알고리즘보다 구현이 어렵지만 DFS 1번으로 SCC를 구할 수 있음.
Strongly Connected Components(SCC)
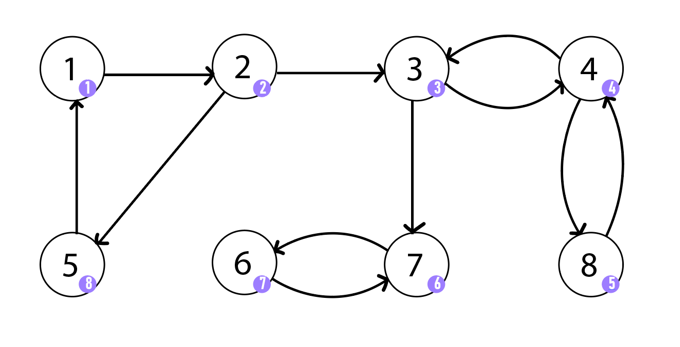
- 위 그림에서 (1,2,5)는 연결되어 있는 동시에 1은 2,5를 방문가능하고 2는 1,5를 방문가능하며 5는 1,2를 방문가능하다. 즉, 모든 정점이 다른 정점에 대해 방문가능하여 SCC이다.
- 한 정점에서 다른 모든정점으로 직접적인 연결이 되어있다는 의미는 아니다.
- 다른 정점을 지나서 도달할 수 있다는 의미이다.
- 하지만 3이 추가될 경우, (1,2,3,5)는 SCC가 아니다.
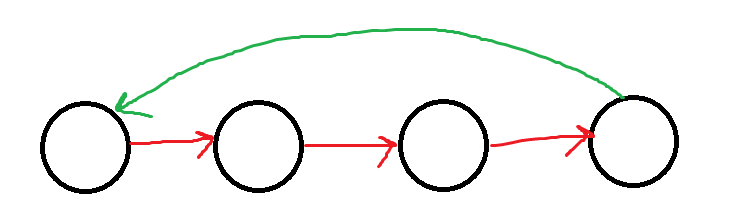
- 즉, SCC는 위처럼 한 노드에서 출발해 다른 노드들을 거쳐 다시 자기자신으로 돌아올 수 있는 cycle을 뜻한다.
과정
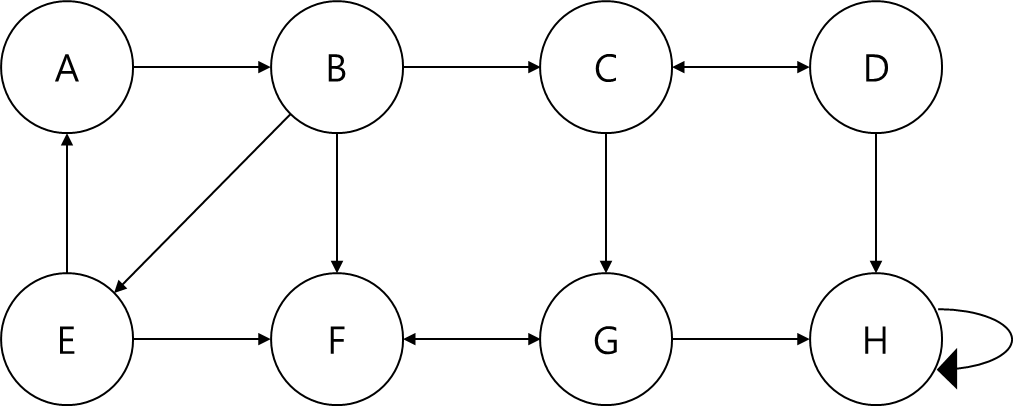
- 위의 그래프를 예시로, 정점 A부터 탐색
- Finished(parents)배열은 SCC판별이 끝났는지 저장
- visited 배열은 해당 정점을 방문하였는지 저장
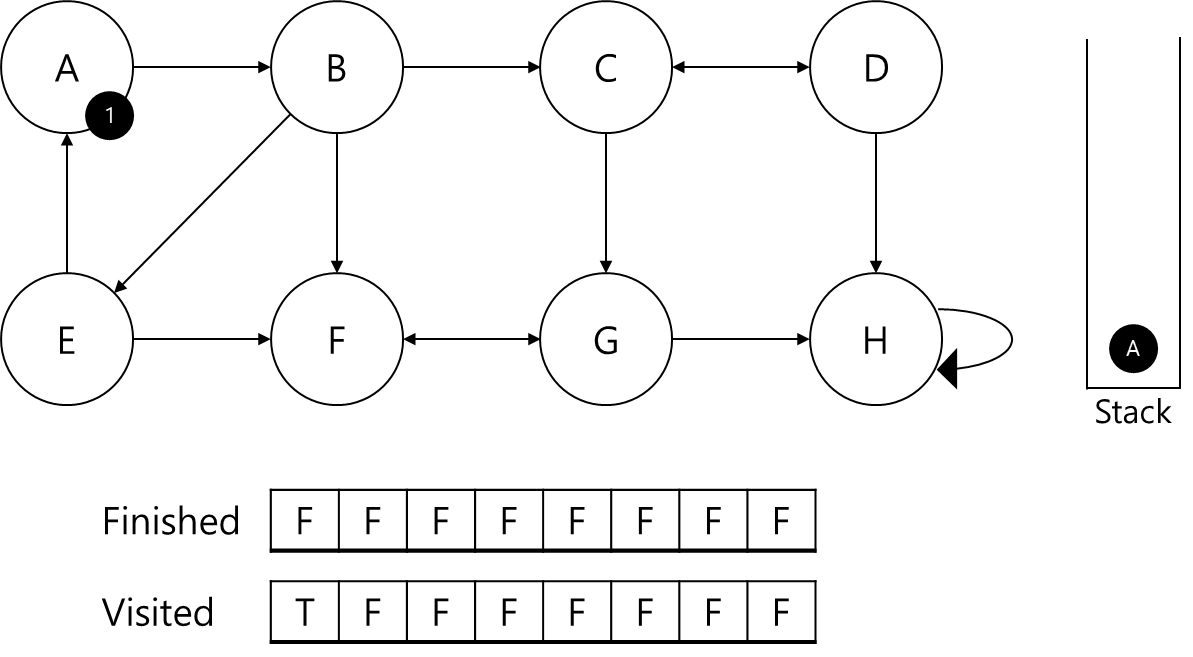
- 먼저, A를 첫번째로 방문했기 때문에 A에 id=1을 부여하고 스택에 삽입
- A의 visited 갱신
- A에서 B로 이동가능함
- B는 탐색이 되어있지 않으므로, A가 부모노드인지 판별불가
- 이후, A에서 이동 가능한 B를 탐색
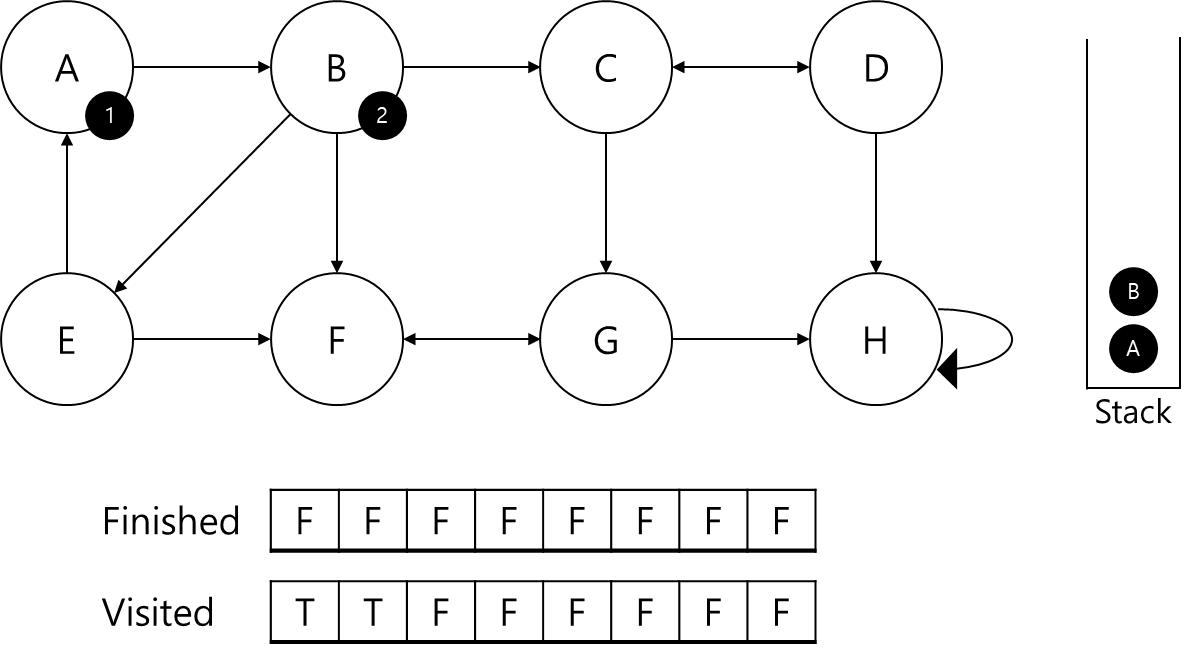
- B에 id=2를 부여하고 스택에 삽입
- B의 visited 갱신
- B에서 C,E,F로 탐색가능
- 각 노드들이 탐색되어 있지 않으므로 B가 부모노드인지 판별불가
- 노드중 가장 작은 C를 먼저 탐색(알파벳순이라고 가정)
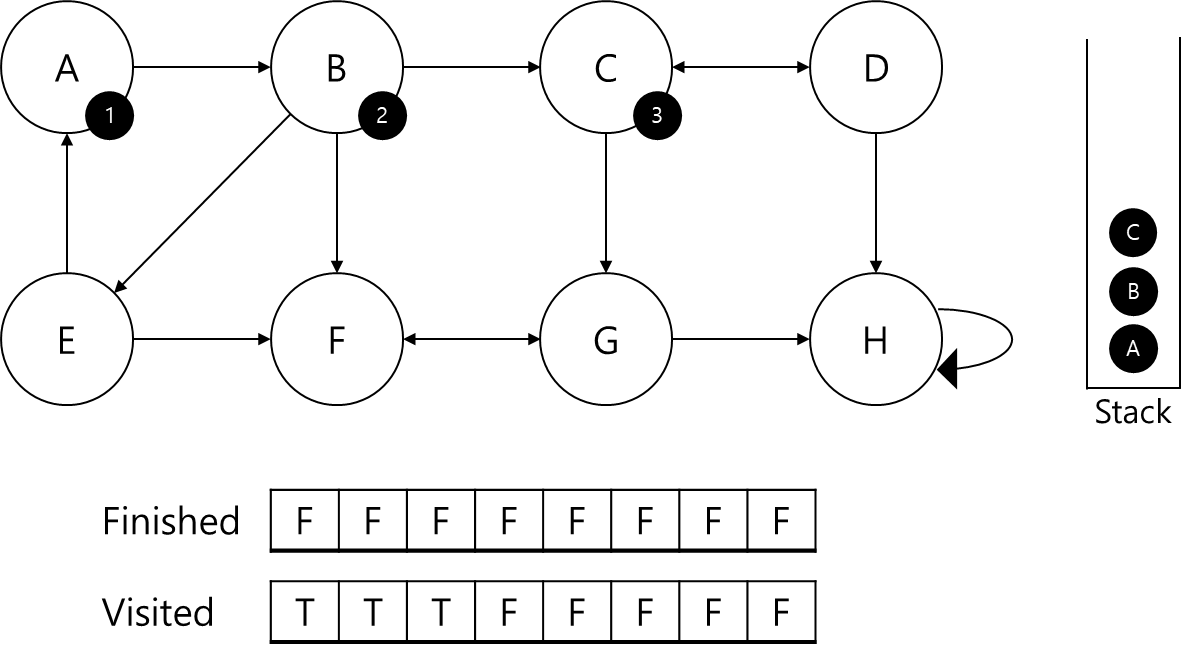
- C에 id=3을 부여하고 스택에 삽입
- C의 visited 갱신
- C에서 D,G로 탐색가능
- 각 노드들이 탐색되어 있지 않으므로 C가 부모노드인지 판별불가
- 노드중 가장 작은 D를 먼저탐색
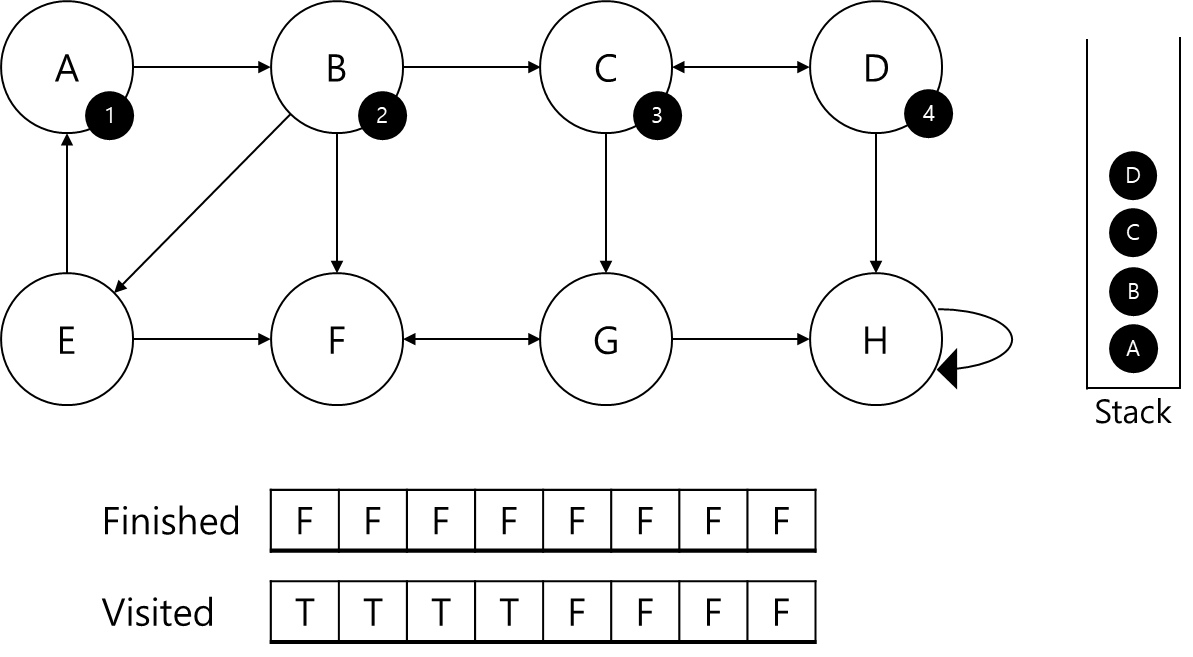
- D에 id=4를 부여하고 스택에 삽입
- D의 visited 갱신
- D에서 H로 탐색가능
- H는 탐색되어 있지 않으므로 D가 부모노드인지 판별불가
- H를 탐색
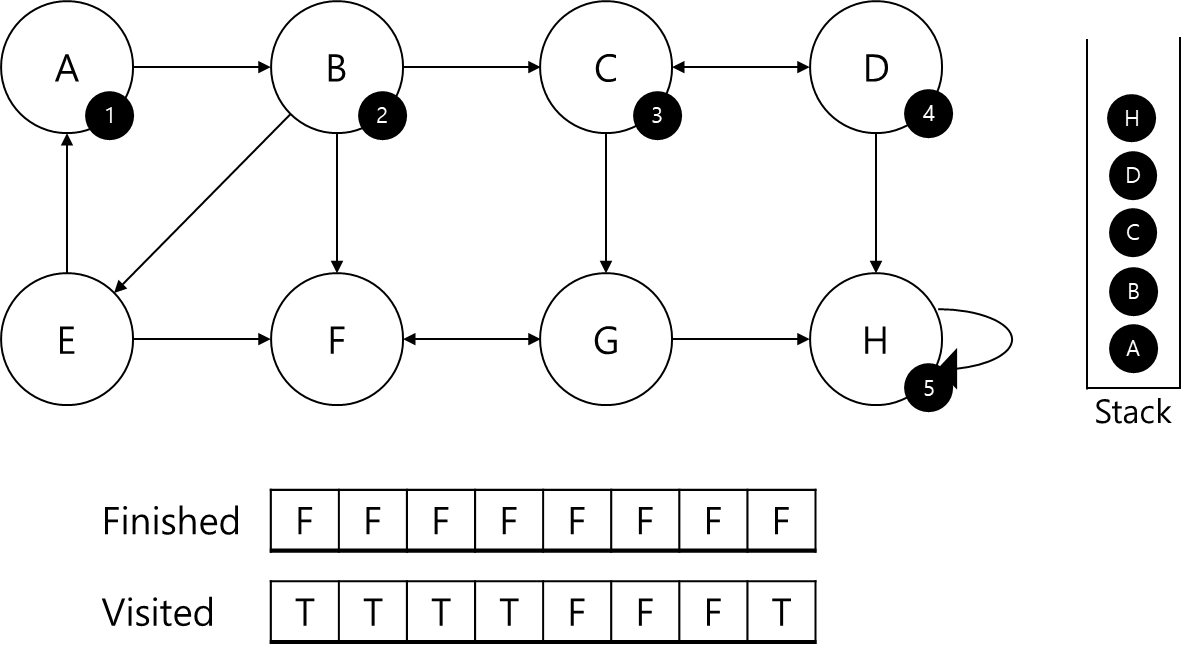
- H에 id=5를 부여하고 스택에 삽입
- H의 visited 갱신
- H에서 H로 이동가능
- H는 탐색되어있음(자기자신)
- 스택에서 부모노드인 H가 나올 때 까지빼내고 Finished 배열을 갱신
- SCC배열에 저장
- 이전으로 되돌아감(D)
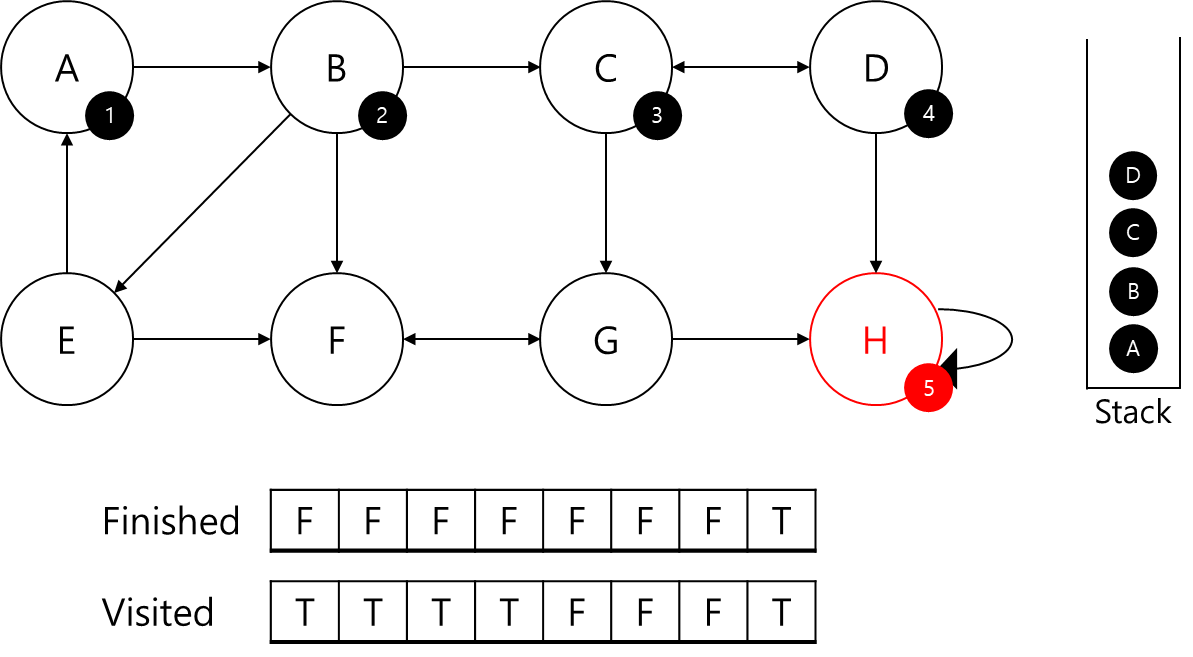
- D와 연결되어 있는 C,H의 부모정점이 본인이 아니기 때문에 본인의 부모인 C를 반환해주고 C로 이동(4≠min(3,5), 3으로 이동)
- C에서 이동가능한 D,G중 D는 방문정보가 있지만 G는 없으므로 G를 방문
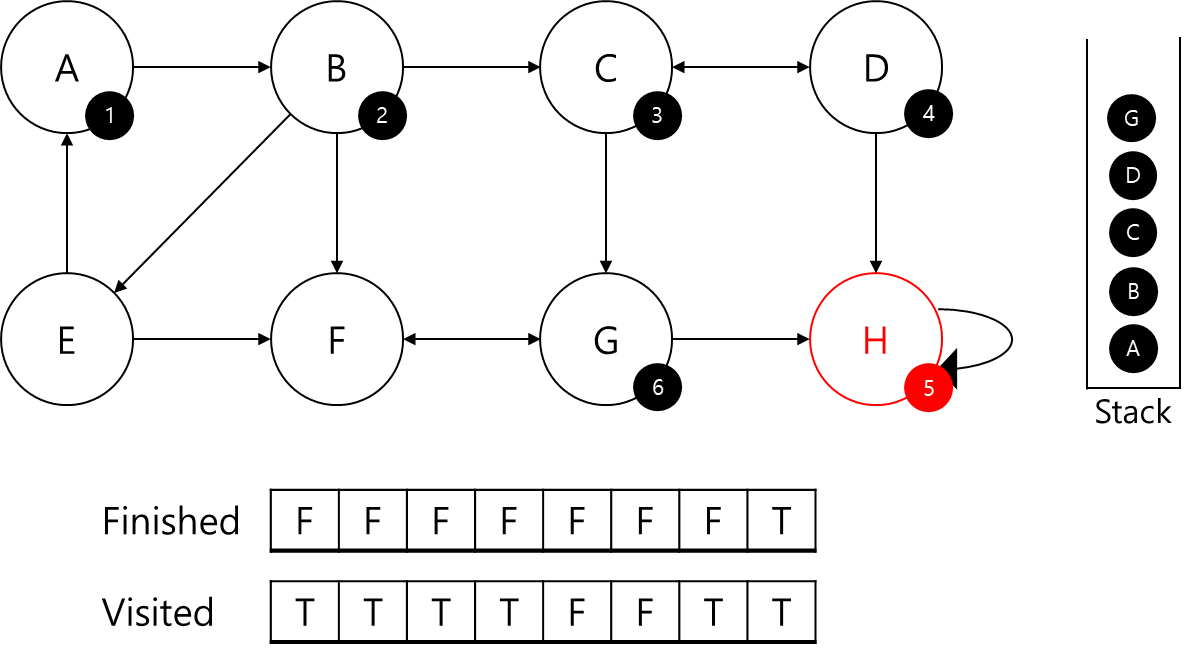
- G에 id=6을 부여하고 스택에 삽입
- G의 visited 갱신
- G에서 F로 이동가능
- F는 탐색되어 있지 않으므로 G가 부모노드인지 판별 불가
- F를 탐색
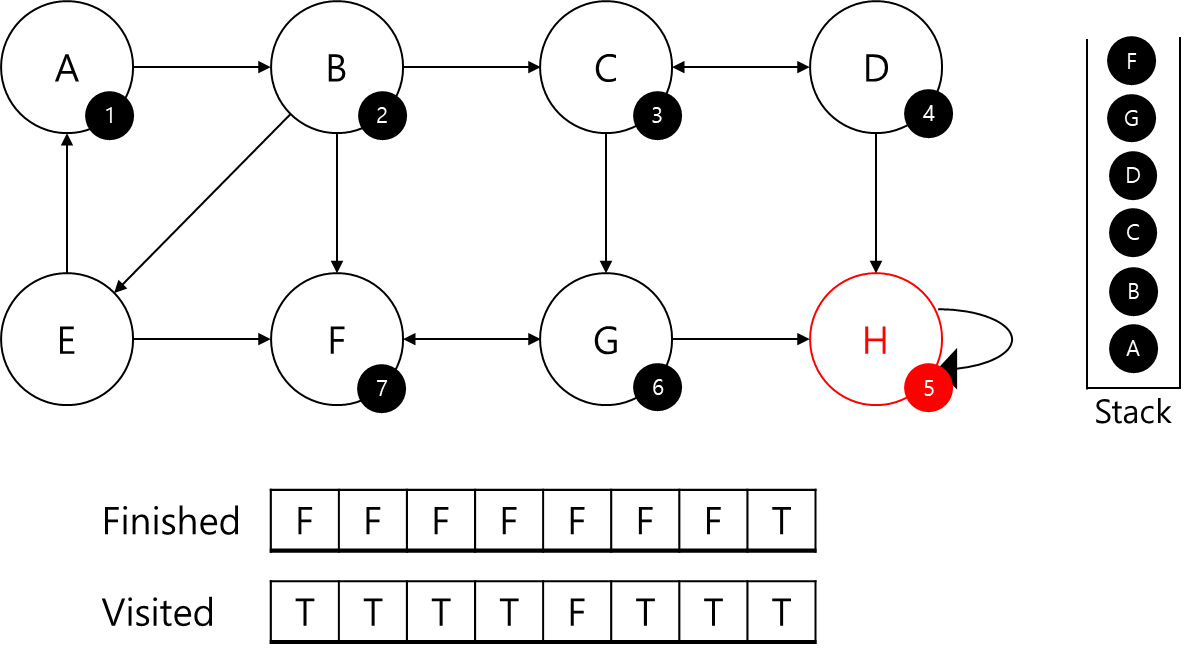
- F에 id=7을 부여하고 스택에삽입
- F의 visited 갱신
- F에서 G를 방문가능한데, G는 이미 방문한 배열이므로, 작은 G를 반환하고 이전으로 이동
- 다시 G로 되돌아왔고, 이제 G에서 F,H의 정보가 있으니 부모정점인지 판별
- F의 부모는 본인(G)이고, H는 이미 SCC이다(Finished되어있음)
- 스택에서 본인이 나올때까지 빼서 SCC에 추가하고 finish배열을 갱신
- 이전으로 돌아감
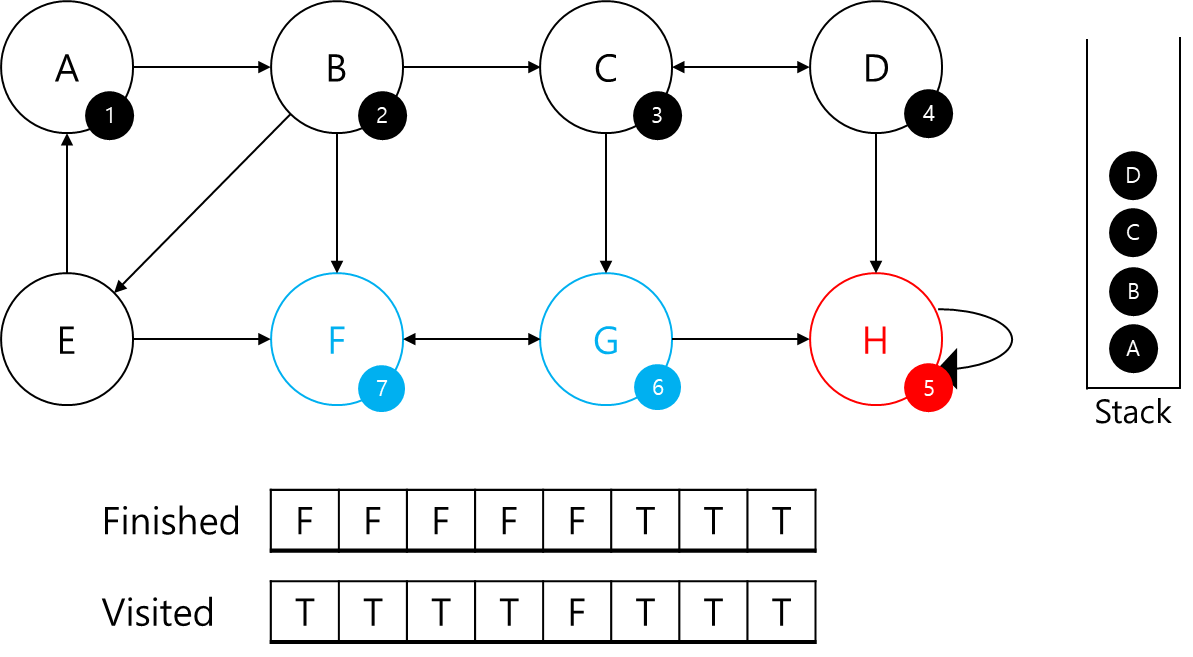
- C에 되돌아와서, 이제 C에서 연결된 G,D의 정보가 있으니 부모정점인지 판별
- D의 부모는 본인(C)이고, G는 이미 SCC이다.
- 스택에서 본인이 나올때까지 빼서 SCC에 추가하고 finish배열을 갱신
- 이전으로 되돌아감
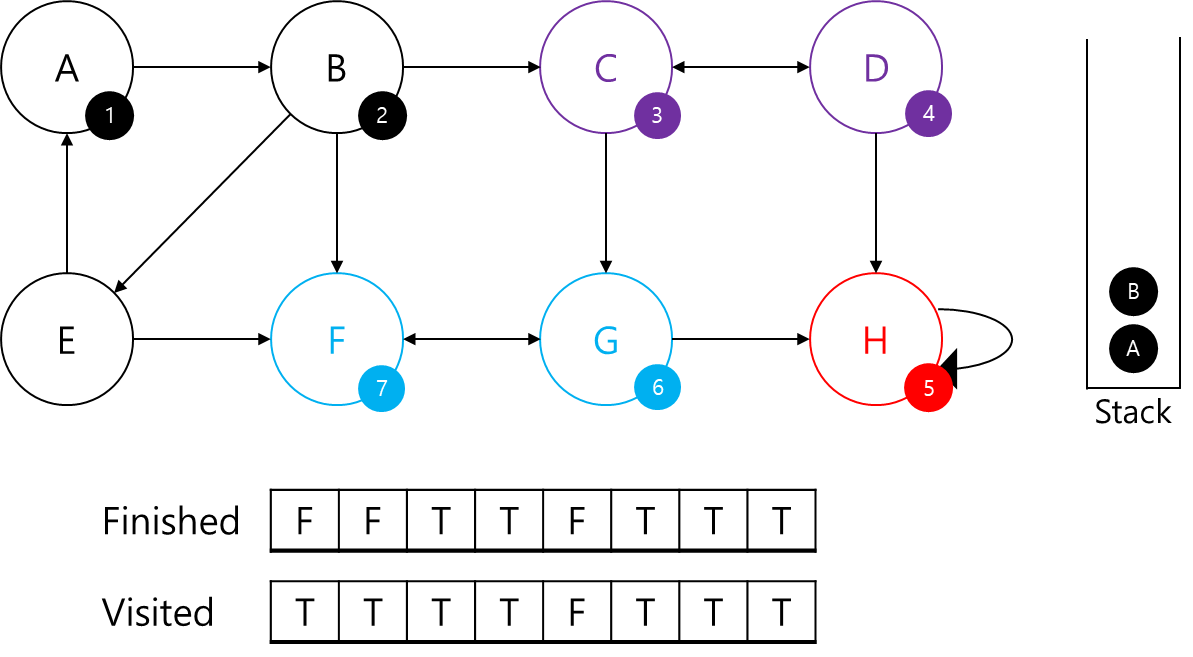
- B로 되돌아와서, 이제 C는 탐색되었지만 E와 F가 탐색되어있지 않음
- E를 탐색
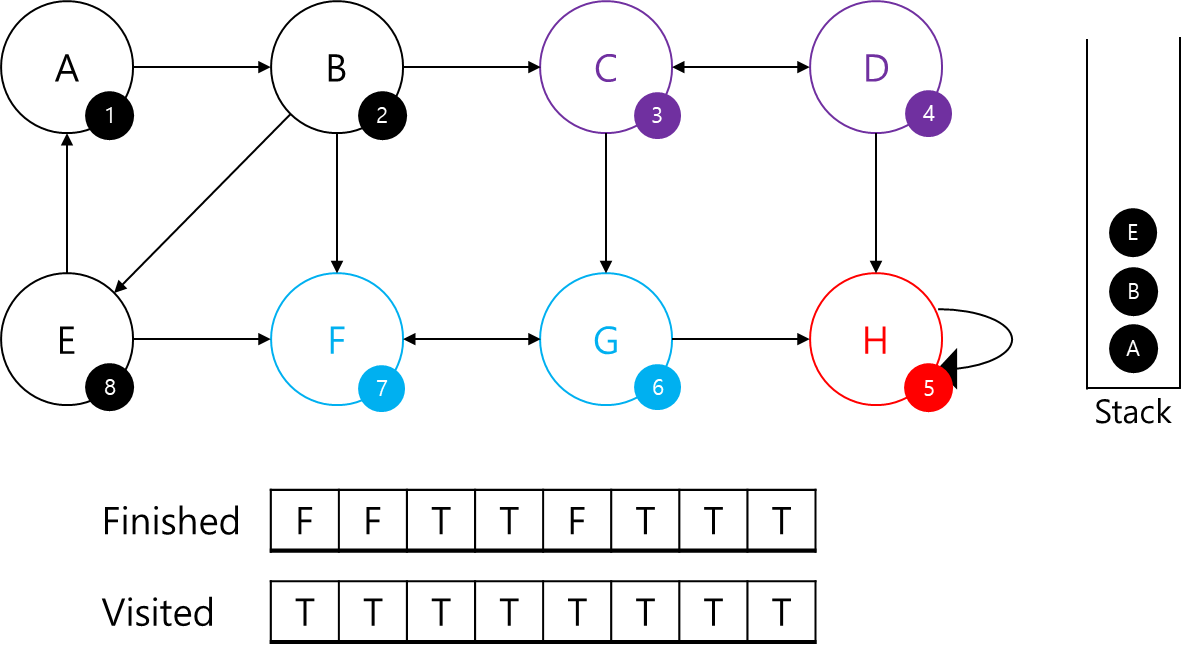
- E에 id=8을 부여하고 스택에 삽입
- E의 visited를 갱신
- E에서 A,F로 이동가능
- A는 방문되어있고, F는 이미 SCC이다.
- 그러므로, 본인의 부모정점인 A 반환(min(1,8))
- 이전으로 되돌아감
- 이제 B에서 본인이 부모정점인지 판별
- C와 F는 이미 SCC이고, E에서 반환받은 부모정점은 본인이 아님.
- 그러므로, 부모정점을 판별(min(2,1)하면 A가 본인의 부모정점이 된다.
- 스택에서 본인이 나올 때 까지 SCC에 추가하고 finished배열을 갱신
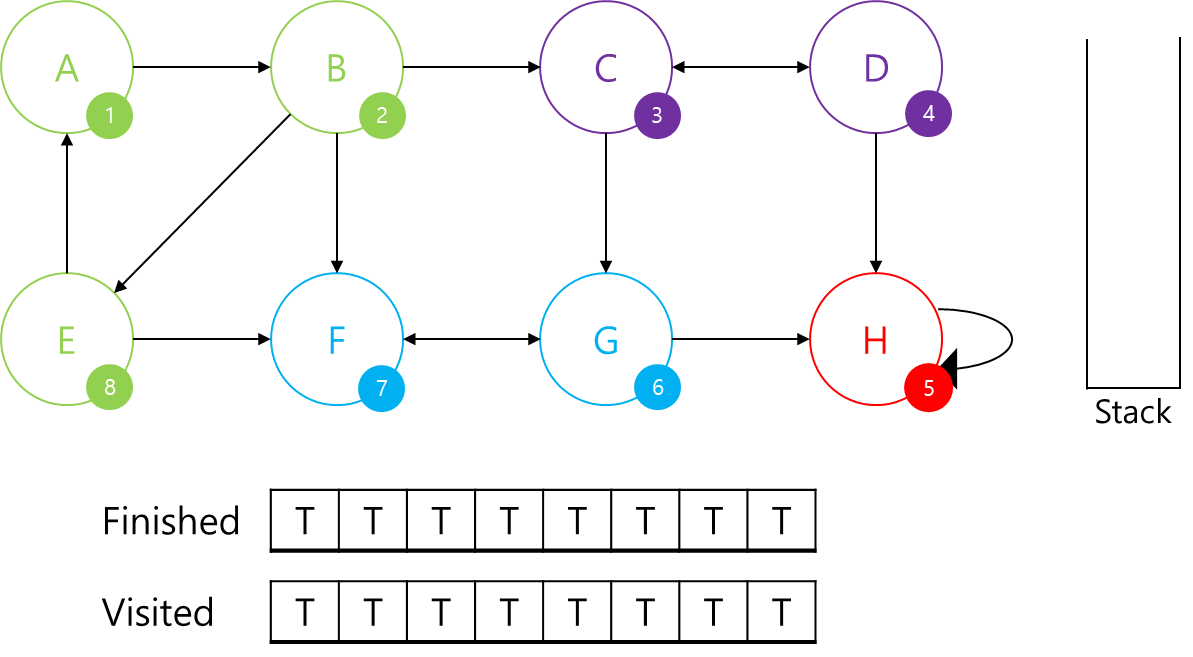
- SCC가 완성되었다.
백준 2150
import sys
sys.setrecursionlimit(10**8)
input=sys.stdin.readline
V,E=map(int,input().split())
graph=[[] for _ in range(V+1)]
parents=[-1]*(V+1)
for _ in range(E):
a,b=map(int,input().split())
graph[a].append(b)
stk=[]
visit=[0]*(V+1)
id=0
res=[]
def func(now):
global id
id+=1
parents[now]=id
stk.append(now)
visit[now]=1
parent=parents[now]
for next in graph[now]:
if parents[next]==-1:
parent=min(parent,func(next))
elif visit[next]:
parent=min(parent,parents[next])
if parent==parents[now]:
scc=[]
while True:
node=stk.pop()
visit[node]=0
scc.append(node)
if now==node:
break
res.append(sorted(scc)+[-1])
return parent
for i in range(1,V+1):
if parents[i]==-1:
func(i)
res.sort()
print(len(res))
for i in res:
print(*i)암기하기 쉽게 변형(백준 11278)
N,M=map(int,input().split())
graph=[[] for _ in range(2*N+1)]
for i in range(M):
x,y=map(int,input().split())
graph[-x].append(y)
graph[-y].append(x)
stk=[]
visit=[0]*(2*N+1)
finish=[0]*(2*N+1)
scc_idx=[0]*(2*N+1)
id=1
scc_id=1
def func(now):
global id,scc_id
parent=id
visit[now]=id
id+=1
stk.append(now)
for next in graph[now]:
if not visit[next]:
parent=min(parent,func(next))
if not finish[next]:
parent=min(parent,visit[next])
if parent==visit[now]:
while stk:
top=stk.pop()
finish[top]=1
scc_idx[top]=scc_id
if top==now:
break
scc_id+=1
return parent
for i in range(1,2*N+1):
if not visit[i]:
func(i)
res=[0]*(N)
for i in range(1,N+1):
if scc_idx[i]==scc_idx[-i]:
print(0)
break
if scc_idx[i]<scc_idx[-i]:
res[i-1]=1
else:
print(1)
print(*res)