SNU 강화학습의 기초(5) Model Free Control,Prediction

Control은 V나 Q를 사용하여 Optimal Policy를 구하는 방법을 뜻한다.
Prediction은 Policy에 따라 V나 Q를 구하는 것을 뜻한다.

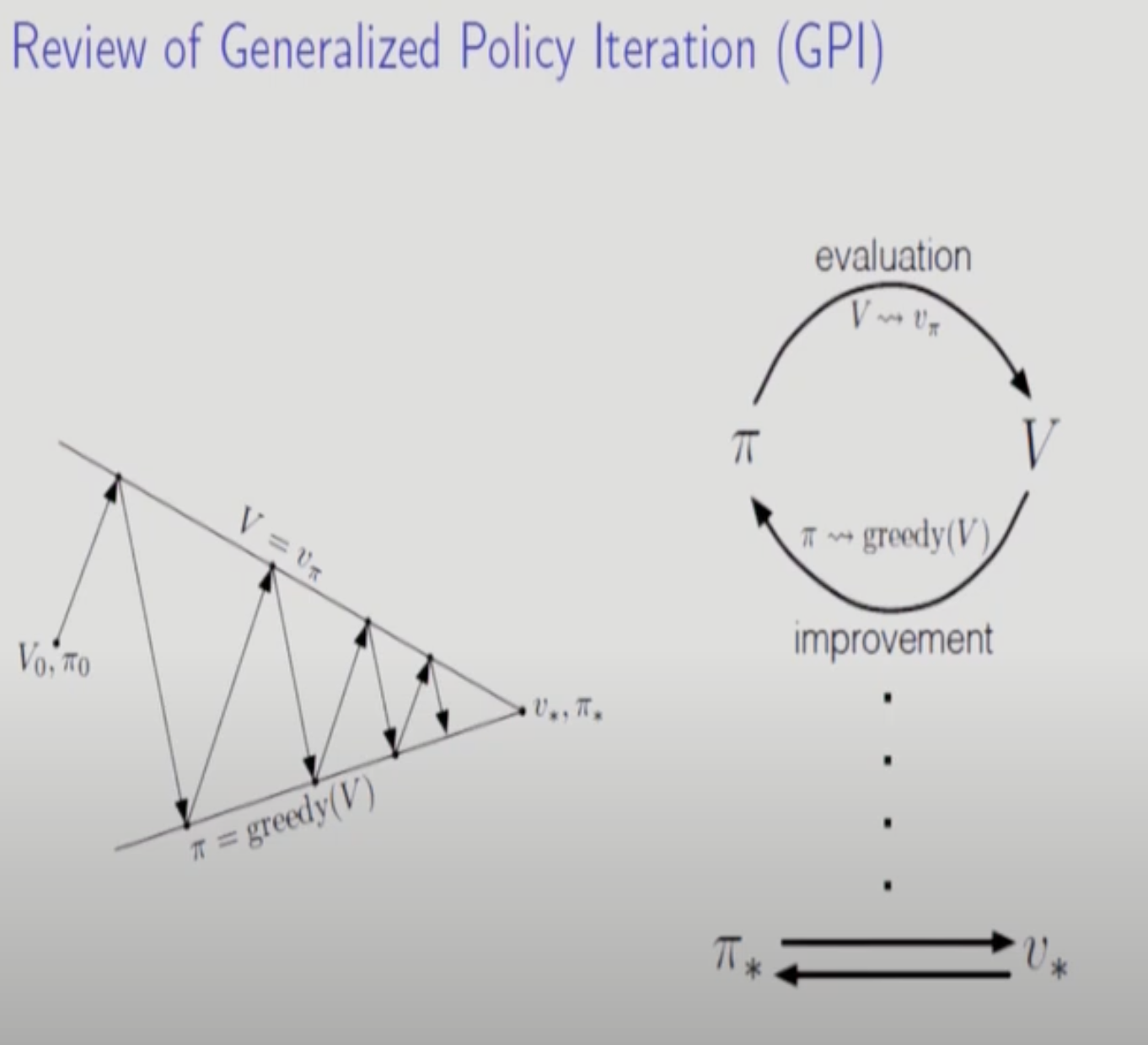
Policy Iteration에 기초를 두고 5장의 모든 알고리즘들이 설명된다.

두 가지 가정이 있다.

• Exploring Starts : 탐험을 하며 시작함 => 실제 세계에서는 어렵다. 우리가 환경을 컨트롤하는 것이 보통 불가능 함으로.
• 무한한 수의 에피소드로 Policy Evaluation을 수행한다. => 유한한 에피소드로 수행했을 때 수렴함이 아직 증명되지 않았다.

MC를 State Value Function으로 구하는 것은 무리이다. 다음 State의 State Value Function를 알려면 미래를 내다봐야 하는 Method인데 MC의 가정이 모델을 모른다는 가정이므로 미래를 볼 방법이 없다. 따라서 Action을 포함한 Action Value Function을 통해서 구한다.

random initial state에서 시작해서 한 episode가 끝날 때 까지 돌린다음에 (s,a) pair가 나온것에 대해서 Return들의 평균을 계산한다. episode에 한 번도 안나온다면 평가가 불가능하다.

Exploration Start를 피해가는 방법이 또 하나 있다.
Episode 중간에 모든 action pair를 다 방문한다는 가정이다. 현실적으로는 비현실적인 가정이긴 하다.

이 방법에서는 Policy가 Deterministic한 Policy로 수렴한다.

현실적인 두 가지 전략은 다음과 같다.

• On Policy
• Off Policy

또한 Deterministic한 Policy의 반대는 Stochastic인데 Stochastic Policy중 일부분으로 state에서 모든 action들에 대한 확률이 Non zero인 Soft Policy가 있다.

앱실론 Soft Policy는 모든 action에 대한 확률이 특정양수보다 큰 Policy이다.

앱실론 Soft안에 앱실론 그리디가 있다.

• 가장 Q function을 최대화 시키는 Action에 1-앱실론의 확률로 확률을 다 몰아주고 나머지 action들이 앱실론의 확률을 나눠갖는 방법. 여기에 최소확률 앱실론/A(s)를 더해준다.

  

On-policy, Off-policy control

Off policy 전략에는 자율주행이 대표적이다. 자율주행에서 운전자의 운전은 Behavior Policy이고 자율주행은 Target Policy이다. Target Policy는 Behavior Policy보다 좋아지는 것이 목적이므로 두 가지가 달라야한다. 따라서 Off-policy이다.

먼저, On-policy 방법을 알아보자.

앞에서 다룬대로 Optimal Policy는 Deterministic하다. 하지만, Deterministic Policy를 처음부터 사용하면 새로운 State에 대해 학습이 되지 않는다. 따라서 Deterministic Policy를 포기한다. 이때 사용하는 개념이 앱실론-Greedy이다. 조금의 오차는 포기하겠다는 전략이다.

앱실론도 학습이 진행될수록 decaying시키면 학습이 더 잘 된다.

앱실론 Greedy를 사용하여 Policy를 update하면 더 나아진다.(On-policy 상황에서)

파이랑 파이프라임이 모든 가능한 앱실론-soft중에 optimal하다.

Off-Policy로 가려면 Importance-Sampling을 해야한다. Ordinary Importance-Sampling와 Weighted Importance-Sampling 중 Weighted가 더 선호됨.

Target Policy는 그리디하게 가져가고, Behavior Policy는 앱실론Greedy를 사용해서 앱실론의 확률만큼 Exploration한다. 두 Policy의 차이는 앱실론 정도이므로 엄청 다르게 진행되지는 않는다. 혹시라도 두 Policy의 차이를 크게 하면 학습이 거의 되지 않으니 조심하자. Q-Learning이 Off-Policy의 대표 학습법이다.

Off-Policy에 대한 설명이다. 에피소드안에 확률이 앱실론이되는 Greedy하지 않은 action(Target에서 벗어나는 action)이 골라지면 해당 에피소드를 다 버려야 한다.(업데이트가 이루어지지 않으므로).

에피소드가 진행되다가 Target과 Behavior Policy가 어긋나는 순간이 나오면 그때까지 계산된 애들을 다 버려야 한다. 하지만 그러다가 다시 Target, Behavior가 일치하면 그 이후로는 쓸 수 있다. 따라서 0->T 방향이 아니라 T->0 방향으로 계산하면 좋다. 이런 방식을 쓰다보니 앞에서 발생하는 Partial Sequence에 대해서는 Learning이 안일어날 가능성이 높다. 그래서 학습속도가 굉장히 slow down된다.

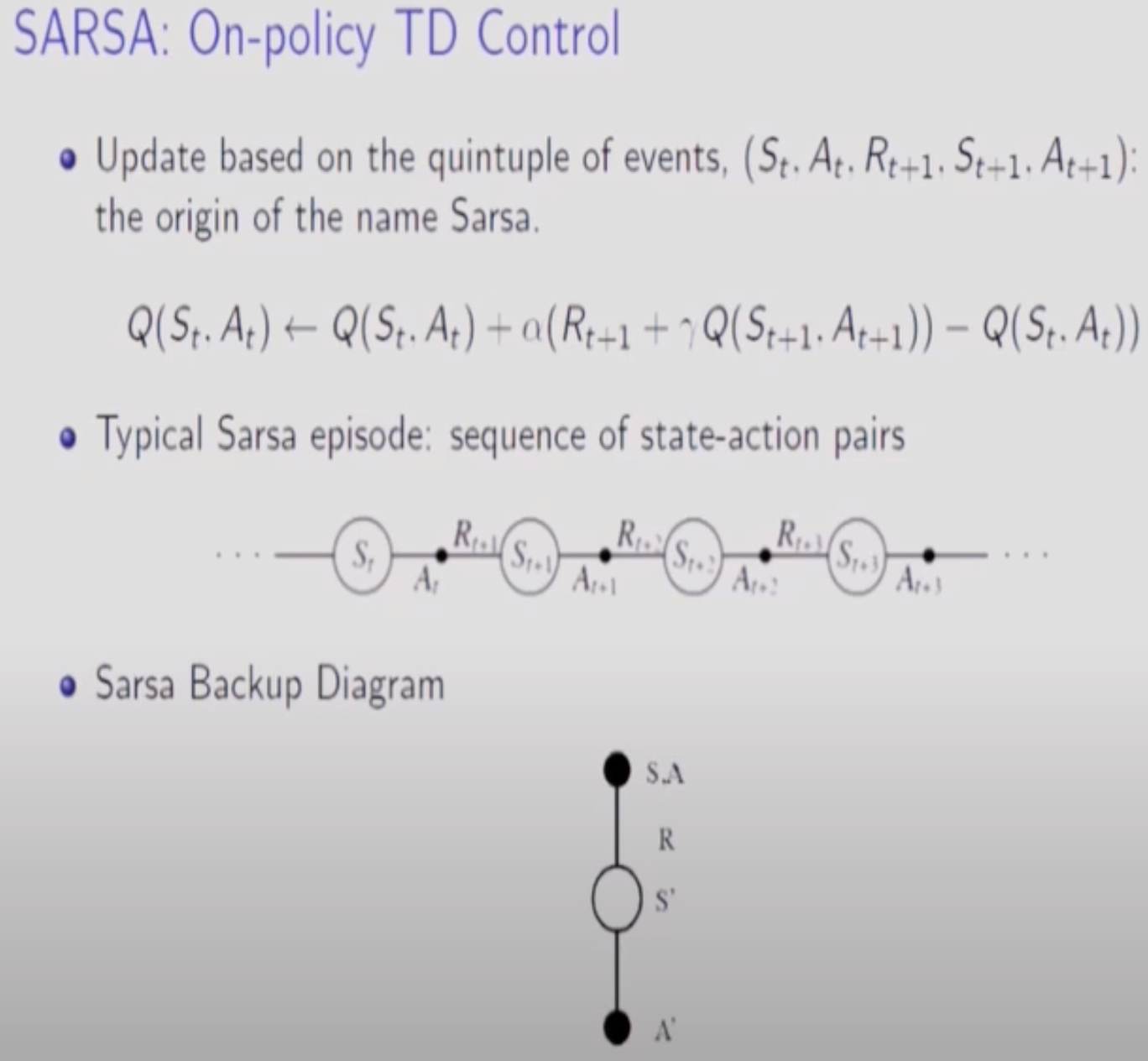
이전에 배운 TD에서는 t+1 타임의 S까지만 알면됐었다.(V를 구하면 됐으므로)하지만, SARSA는 Q-Function을 구해야하므로 Action을 구해야 한다. 즉, TD에서 V를 Q로 바꾼게 SARSA이다. Optimal Policy를 구하고 Exploration도 해야하는데 하나의 Policy로만 학습시키는 방법은 앱실론 그리디가 가장 효율적이다.

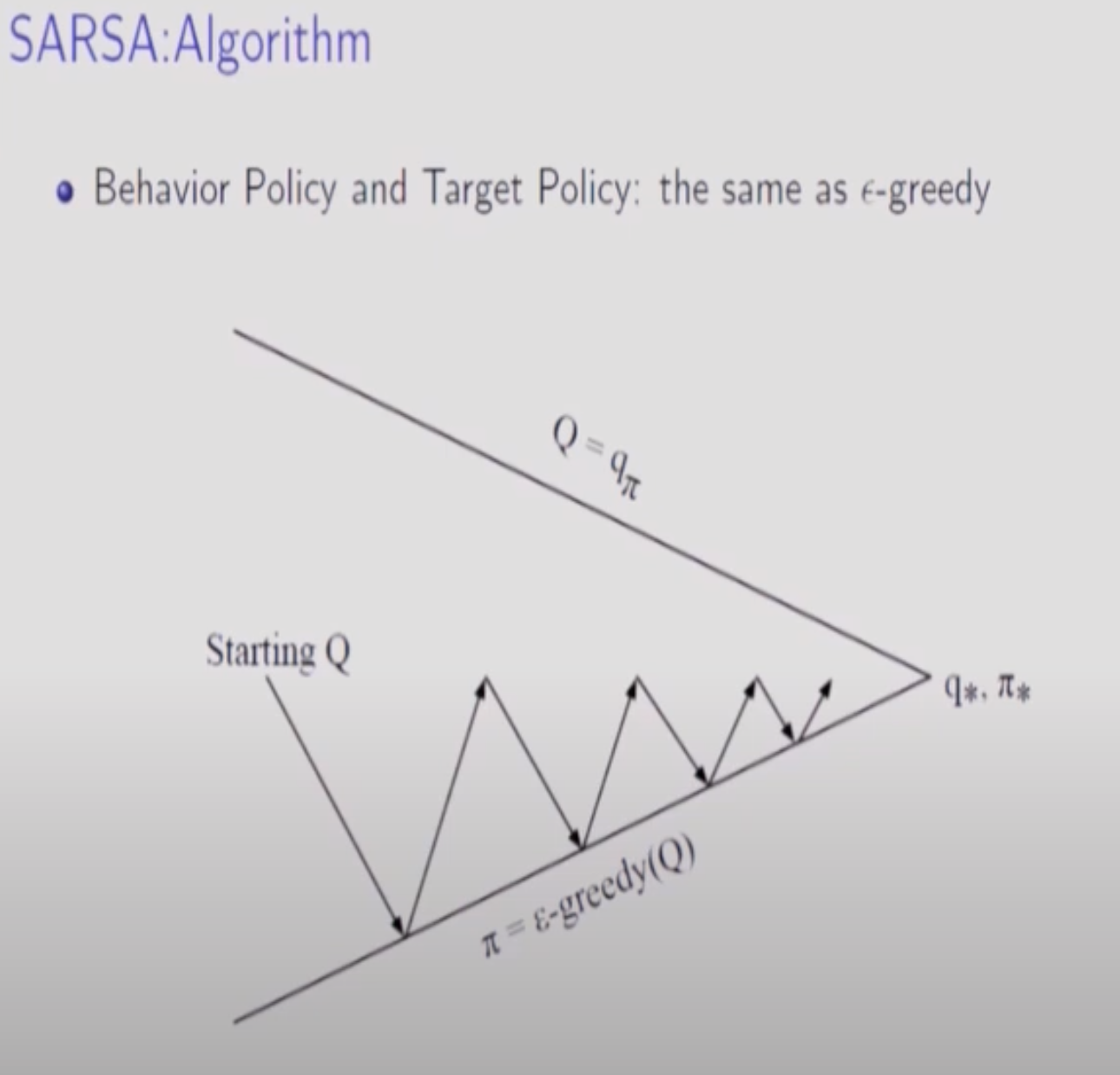
모든 S,A에 대해서 Update한 것도 아니고(Greedy하게 1Step만 진행하고 Episode에 나온 S,A Pair에 대해서만 진행되므로), 수렴할 때 까지 진행하지도 않으므로 화살표가 끝까지 가지않는다.

SARSA가 Converge한다는 증명이다.

N-Step TD에서 V만 Q로 바뀐다.

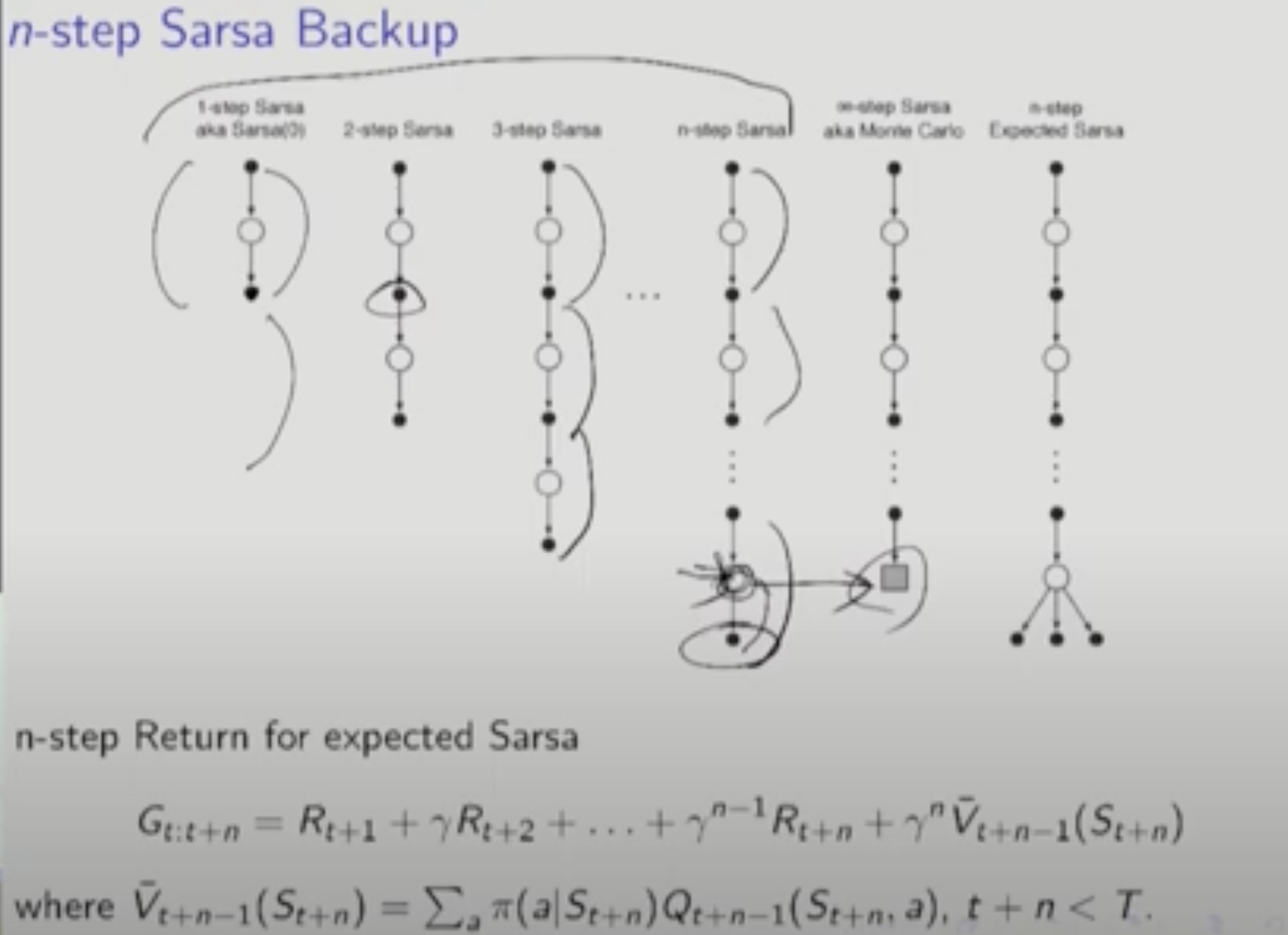
N-Step Expteted SARSA
=> 마지막 state에 대해서는 모든 action의 평균을 취한다. 이것을 V바로 표현한다. 마지막 state의 모든 action을 고려하므로 N-Step TD보다 정확성이 높아진다. 마지막 State 전까지 만들어진 Model을 가지고 가능한 Q-Function의 평균을 취하는 것.

마지막에서 3개, 2개 등 다양한 변종 알고리즘을 만들 수 있다.

Terminal State에 얼마만큼의 시간 이후에 도달할지 모르니까 T를 무한대로 놓는다. 그리고 n에 도달하기 전까지는 Policy를 Update하지 않고 Data(State, Action)만 모은다. 그리고 타우를 t-n+1(Terminal State도달한 시간 t에서 n-1만큼 back)로 정의하고 타우가 0보다 커지면 N-Step SARSA를 진행한다.
T-n부터 T까지의 구간은 N-Step Return의 항의 개수가 하나씩 줄어든다.

n-step Off-policy에 TD를 사용한 알고리즘이 있고 SARSA를 사용한 알고리즘이 있다.

TD를 사용한 Off-Policy와 SARSA를 사용한 Off-Policy의 다른점은 Importance sampling ratio 범위이다. p의 범위는 TD에서 t~t+n-1 까지였다. 이게 n-step Off-Policy에서는 t+1~t+n으로 바뀐다. t->t+1로 바뀌는 이유는 Q function을 사용하기 때문인데, 현재 state에서의 action a는 deterministic하게 주어지는 것이고 그 다음 step에서의 a를 sampling 하는 것이기 때문이다. deterministic하게 주어지는 값 a에 대해서는 확률이 1이기 때문에 sampling ratio를 구할 필요가 없다.

SARSA 알고리즘도 TD와 마찬가지로 람다를 적용할 수 있다.(평균)

Return값을 Exponential Weighted Avg로 구한다.

앞에서 다룬 Forward-view TD람다와 마찬가지로 Off-line 알고리즘이며 한 에피소드가 끝나야 Policy를 update할 수 있다.

Prediction문제에서 TD를 다루던 방법론이 Control 가면 SARSA가 되는 것이다. TD를 좁은 의미로 사용하면 V를 구하는 Approach이다. 넓은 의미로 사용하면 미래에 대한 Prediction과 현재값과의 차이를 통해 V또는 Q를 구하는 일반적인 방법론을 칭한다. 따라서 SARSA도 넓은 의미로는 TD에 속한다 할 수 있다.

Eligiblity Trace를 사용하여 Backward-View로 바꾼다. E는 앞에서 다뤘듯이 최근에 발생하거나 많이 발생한 S,A Pair에 높은 가중치를 부여한다.

Backward-view SARSA람다 On-Policy이다.

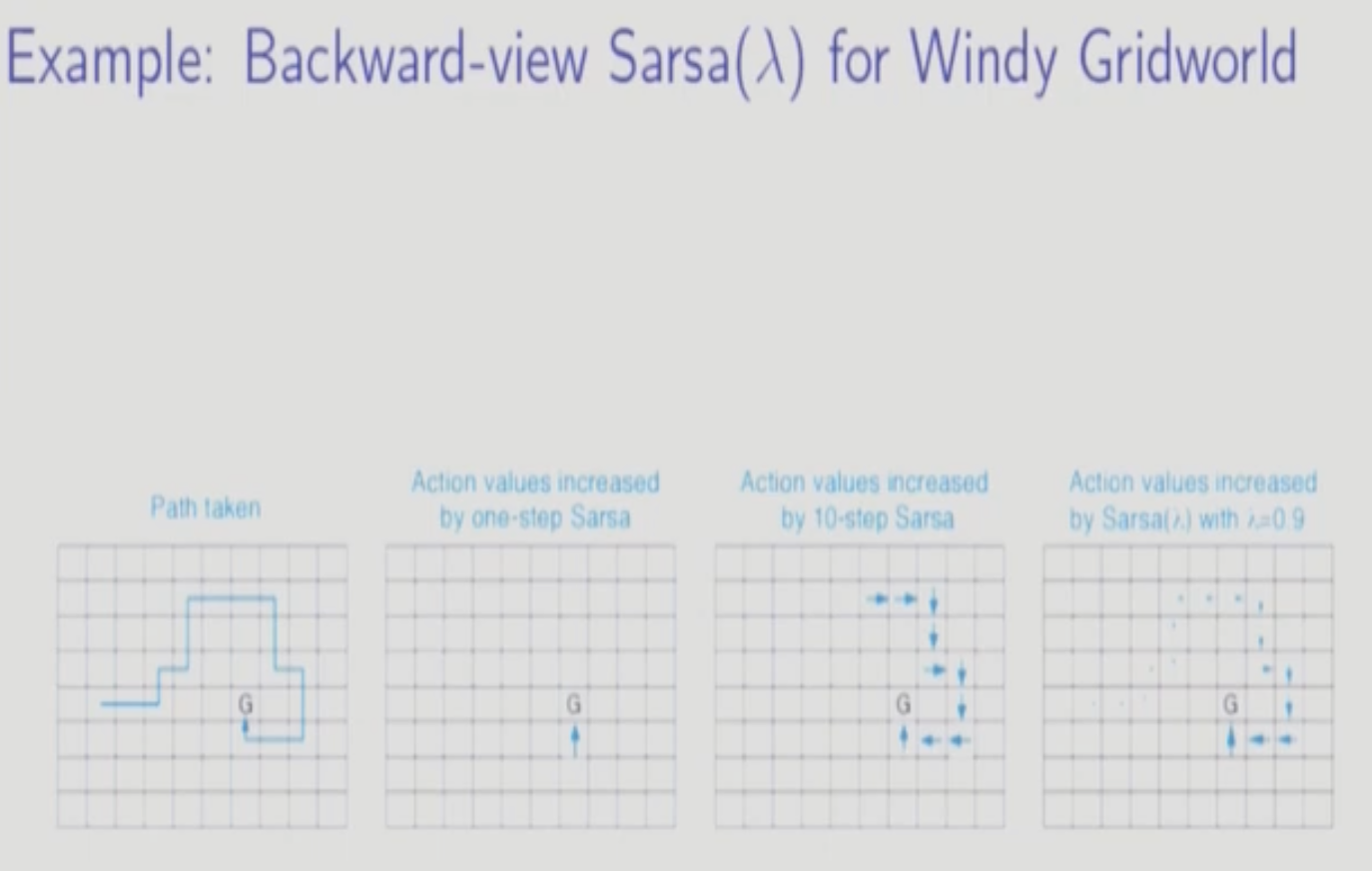
오래전에 발생한 S,A Pair에 대해서는 Decaying Factor가 누적되어 Update가 작게 일어난다.

Q-Learning

Behavior Policy에서는 앱실론-Greedy를 사용하고 Target Policy에서는 Greedy한 학습법을 사용한다.

Importance Sampling ratio를 곱하지 않는 이유는 Next state t+1에서 실제 action을 취하지 않고 Q가 최대가 되는 a만 계산하기 때문이다.

Value Iteration관점에서 1-Step 진행될 때마다 바로바로 Greedy한 update가 진행된다고 생각하면 된다.

Q-learning은 exploration을 하지 않으므로 수렴 정확도 측면에서 SARSA보다 우월하다. 하지만 이는 무한대로 학습을 진행한다는 가정이 있을 때 이다. 무한대가 아니고 중간에 학습을 끝낼 경우 SARSA가 더 정확도가 높을 수 있다.

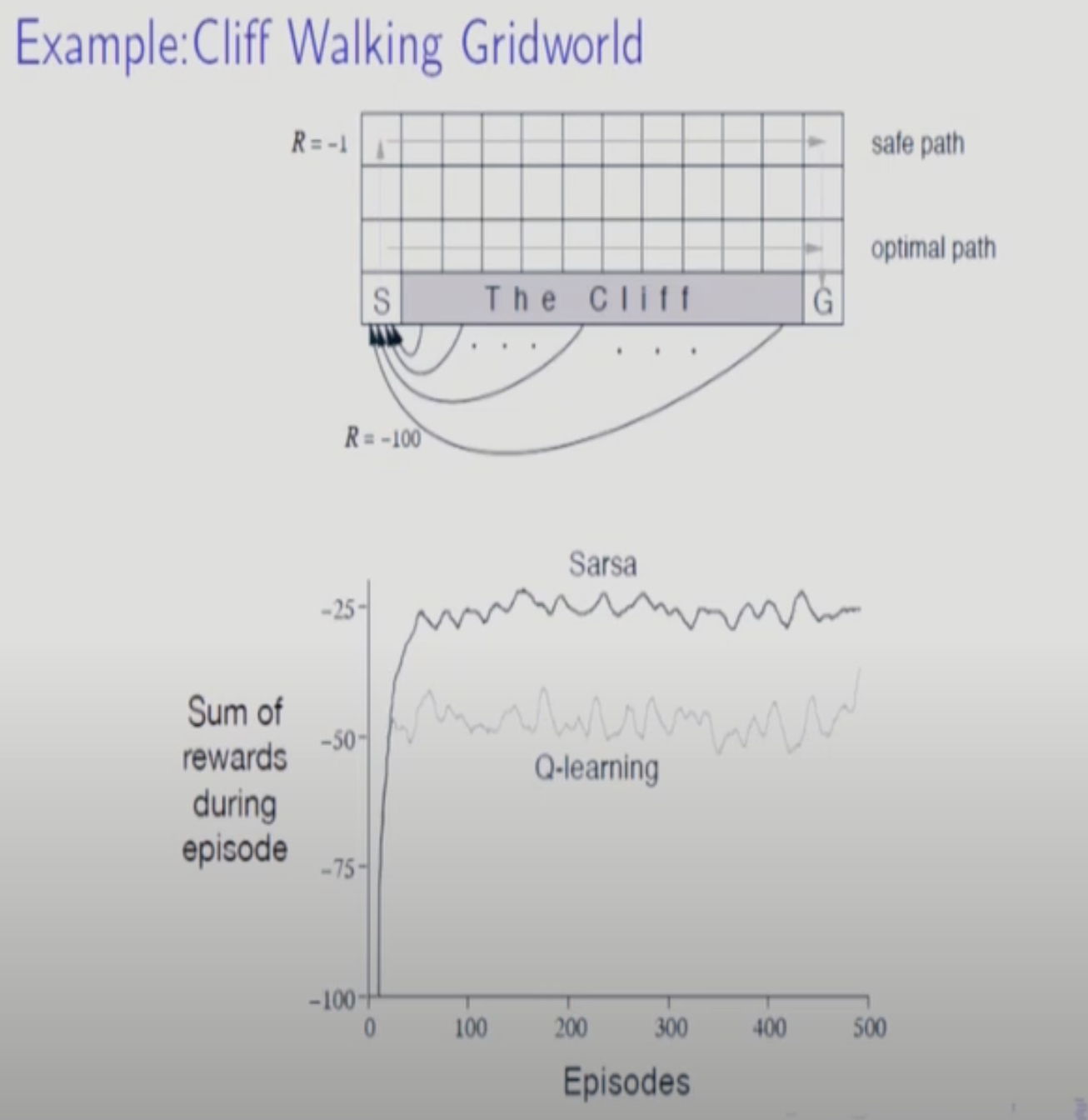
특히 다음과 같은 예제에서 SARSA가 더 빨리 수렴하는데 SARSA는 Q-function을 통해 1-Step 미래를 본다.

이런 예제와 같이 극심한(?) state가 있을경우 안전한 SARSA를 쓰는게 낫다.

SARSA와 Q-Learning을 포함하는 개념인 Expected SARSA가 있다. 앞에서도 다뤘다. 마지막 state에 대해서는 가능한 모든 action에 대해 평균을 취하는데 마치 DP처럼 학습하는 것이다.

Q-Learning을 포함한다고 말하는 이유는 Q-function을 maximize하는 a의 확률을 1로두고 나머지를 0으로 두면 max시키는 것과 같아지기 때문이다.

Cliff Example에서 다룬 단점 말고도 Q-Learning의 단점이 하나 더 있다. Maximization과정에서 Bias가 생기는 것이다.

Q-Function을 두 개 쓰고 하나의 Q-function의 action이 다른 Q-function을 Max시키는 방향으로 학습시키면 Bias를 줄일 수 있다.

두 Q-function을 확률적으로 update해준다.