CS224W #3 Node Embeddings

이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.

---

이전 글에서는 Graph 데이터를 처리하기 위한 전통적인 Machine Learning 기반 방법론들을 살펴봤다면, 이번 글부터는 본격적으로 Deep Learning을 활용한 방법론에 대해 알아보려고 한다.

이번 글은 Deep Learning을 활용하기 위한 첫 단계인 Node Embeddings에 관한 내용이다.

1. Node Embeddings

전통적인 ML 기반 방법론에서는 Graph 데이터를 처리하기 위해, Feature Engineering을 통해 데이터를 잘 표현할 수 있는 Feature를 생성하고 이를 ML 알고리즘을 통해 학습시켜 Task를 처리하였다.

다만 이러한 Feature는 우리가 수행하고자 하는 Task에 종속되어 매번 달라지고,
따라서 매번 Feature Engineering을 수행해야 하는 문제점이 존재한다.

이후 Task에 독립적인(Task-independent) Feature를 보다 효율적으로 만들기 위한 방법들이 연구되었고, 이를 위한 방법이 바로 Node Embeddings 이다.

1) Concept

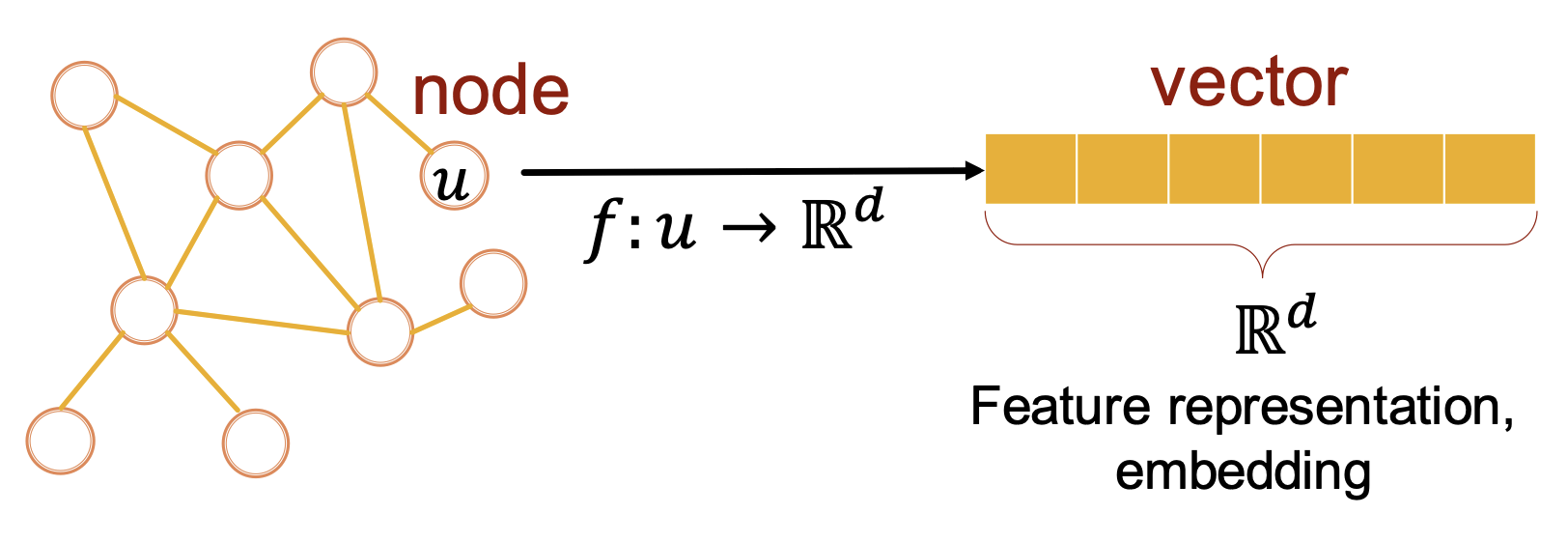
아래 그림을 통해 전체적인 Concept을 먼저 살펴보자면,
개별 Node를 각각 Encoding하여 임의 차원 Embedding space로 Mapping 하는 과정을 볼 수 있다.
(ps. 이때 Graph에 대한 정보는 별도의 Feature가 아닌 Node list / Adjacency matrix만 사용한다.)

여기서 특정 Node를 Mapping 하는 Embedding space의 위치는,
Graph 내 주변 Node와 Similarity 값을 최대로 추정할 수 있는 위치에 Mapping 하는 것을 목표로 한다.

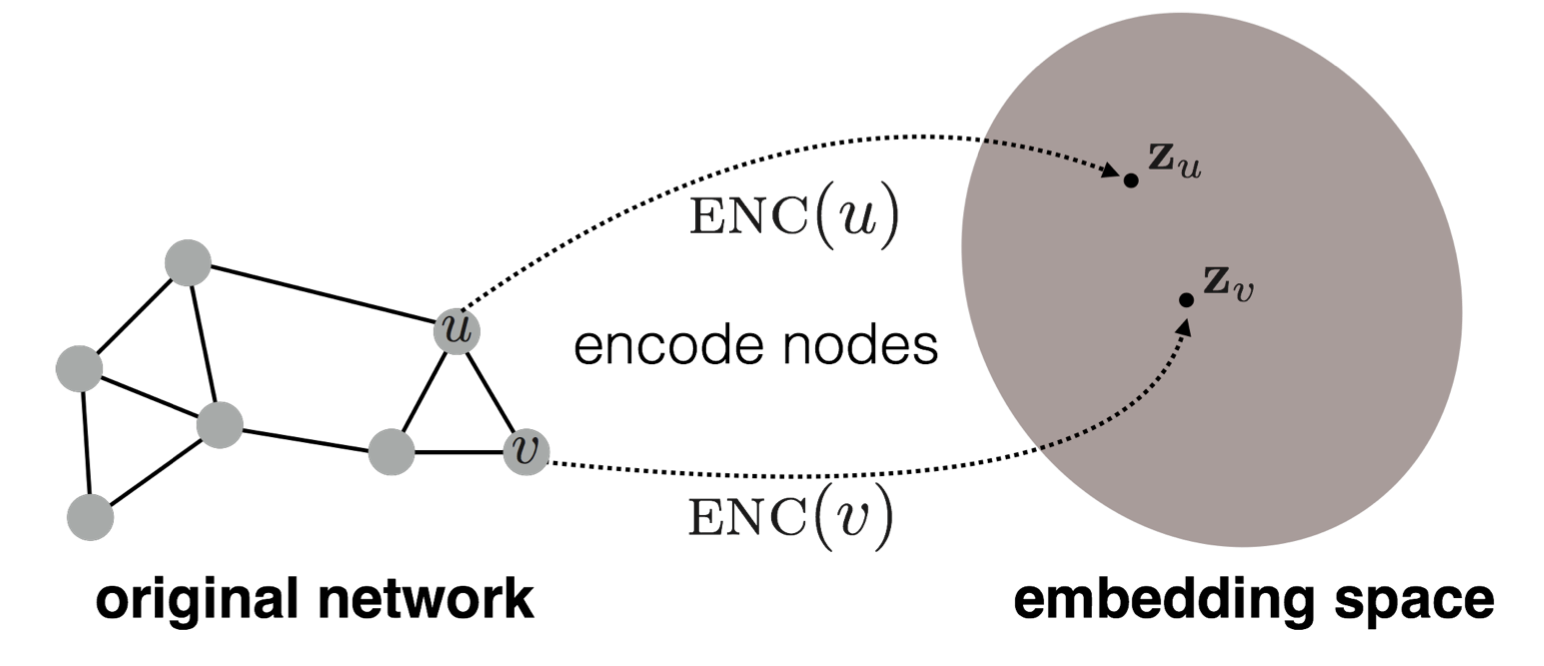
2) Components

위의 그림에서 볼 수 있는 Encoder 와 앞서 언급했던 Similarity function 은
Node Embedding 과정에서 가장 중요한 요소라고 말할 수 있으며, 이 외에 Decoder 도 존재한다.

① Encoder
Encoder는 각각의 Node를 임의의 $d$ 차원의 Vector로 Mapping 하는 요소이다.

② Similarity function
Similarity function은 기존 Graph 내에서 Node 간 Similarity 를 측정하는 요소이다.

③ Decoder
Decoder는 Encoder에 의해 Embedding 된 Vector로부터 Similarity Score를 구하는 요소이다.
이때 보통 Vecotr 간의 유사도를 측정하는 방법인 Dot Product를 사용하기도 한다.

3) Shallow Encoding

그렇다면 Node를 어떻게 임의의 차원으로 Encoding 할 수 있을까?
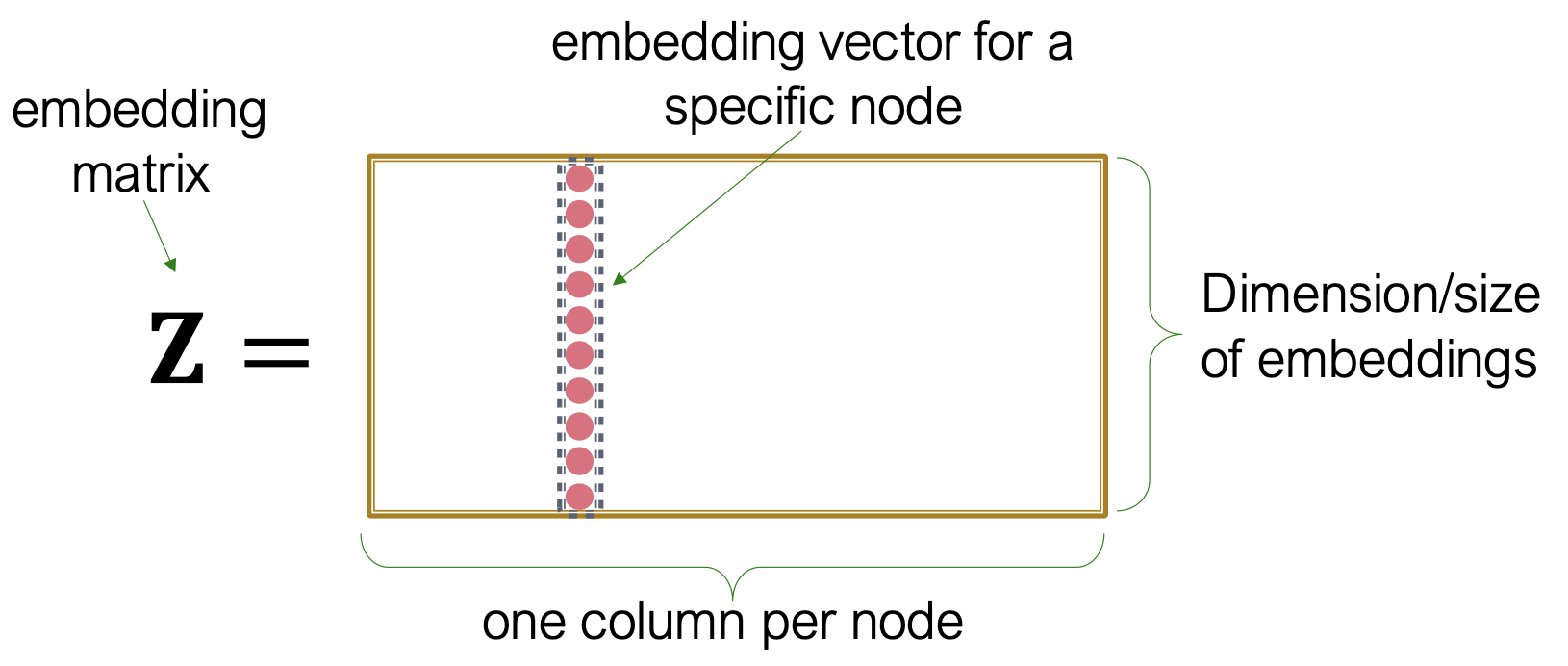
단순한 접근으로, 아래와 같이 Node별로 특정 값을 담고 있는 행렬을 통해 Encoding 하는 방법이 있다.

이때 Node는 해당 Node 위치 외의 값은 모두 0을 갖는 단위 Vector로 표현한다.

그럼 아래와 같이 행렬 $\textbf{Z}$ 는 Embedding Size $d$ X Node 개수 $|V|$ 의 크기를 가질텐데,
Graph의 크기가 작을때는 이러한 방식으로 접근이 가능하겠지만, Node 수가 많아지면 각각의 최적값을 찾아내는 것이 쉽지 않기 때문에 대규모 데이터셋에 확장이 어렵다는 단점이 있다.

이러한 단점을 해결하기 위해 각각의 Node가 고유의 Embedding Vector로 할당되는 Concept을 바탕으로 보다 효율적인 Embedding 방안을 알아보고자 한다.

---

2. Random walk approches

먼저 Random Walk 방식은, 직관적으로 거리가 가까운 Node를 서로 유사(Simliar)하다고 가정한다.
가정을 바탕으로 특정 Node로부터 주변의 이웃 Node를 무작위로 선택하여 이동하는 과정에서 얻게되는 방문한 Node Sequence를 활용하는 방안이며, 자세한 내용은 아래 본문에서 이어서 설명하겠다.

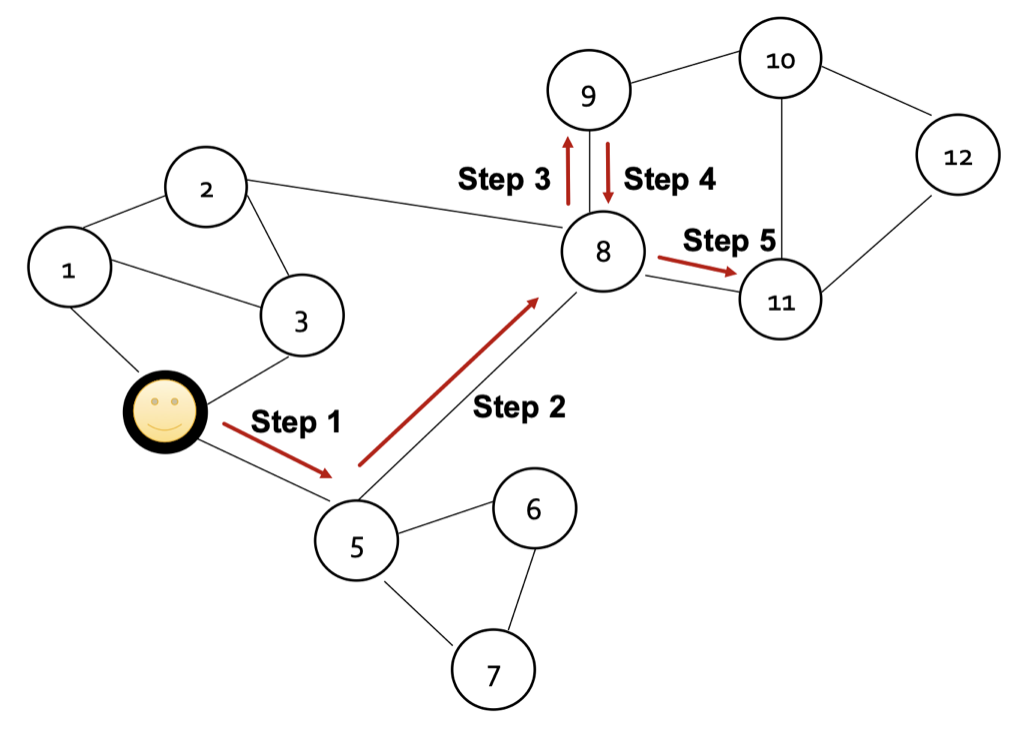
1) Notation

여기에서는 Embedding의 요소 중 하나인 Simliarlity Function으로 확률을 사용하며,
Random walk 과정을 통해 해당 확률을 측정할 수 있다.

Symbol	Description
$\mathbf{z}_u$	Node $u$의 Embedding vector
$N_R(u)$	Node $u$로부터 Random walk를 통해 방문한 이웃 Node의 집합
$P(v \mid \mathbf{z}_u)$	Node $u$로부터 Random walk를 통해 방문한 이웃 Node에 Node $v$가 포함될 확률
$\mathbf{z}_u^{\top}\mathbf{z}_v$	Embedding 된 두 Node 사이의 내적(Similarity) (≈Decoding) (한 Node 시퀀스 내에 Node $u$, $v$가 함께 등장할 확률을 유사도로 추정한다.)

확률을 구하기 위해서 Non-linear Function을 사용하는데, 아래는 그 중 하나인 Softmax Function이다.

2) Optimization

앞서 Simliarity Function으로 Random Walk를 통해 얻어진 확률을 사용한다 언급했으며,
Encoder는 Embedding vector의 값이 해당 확률을 최대로 추정할 수 있게 하는 Function이어야 한다.
이러한 Encoder를 만들기 위한 최적화 방법을 아래에서 다루고 있다.

Objective Function
먼저 아래의 좌항은 확률을 최대로 추정하기 위한 Log-Likelihood 함수이며, 우항은 경사하강법에 사용할 수 있도록 Negative Log-Likelihood 형태로 변환한 것으로 좌항에 대한 동치이다.

여기서 $P(v|\mathbf{z}_u)$는 아래의 수식에서 볼 수 있는 것처럼 Node $u$와 이웃 Node $v$의 Embedding Vector간 유사도가 전체 Embedding Vector 유사도에서 차지하는 비율을 통해 구하고 있으며, 이를 최대화함으로써 이웃 Node는 가까운 위치에, 이웃 Node가 아니면 먼 위치에 Embedding 하게끔 함수를 설계하였다.

$P\left(v \mid \mathbf{z}_u\right)=\frac{\exp \left(\mathbf{z}_u^{\mathrm{T}} \mathbf{z}_v\right)}{\sum_{n \in V} \exp \left(\mathbf{z}_u^{\mathrm{T}} \mathbf{z}_n\right)}$

위의 식을 종합해보면 아래의 목적 함수를 얻을 수 있는데 전체 노드 간의 유사도와 확률을 구하기 위해서(수식의 빨간색 부분), 목적 함수의 시간복잡도가 $\text{O}(|V|^2)$되고 Node의 개수가 많아질수록 비효율적이라는 문제가 있다.

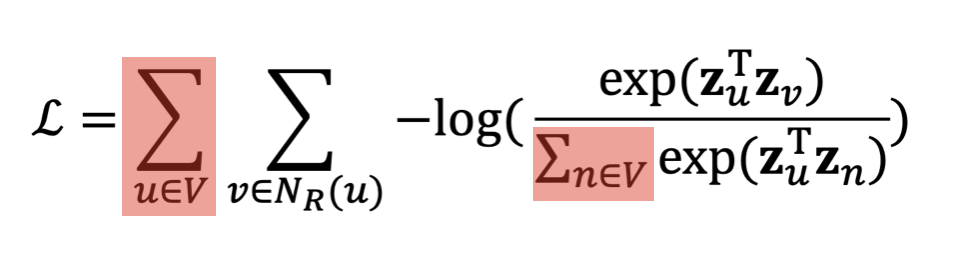
3) Negative Sampling

기존 목적 함수의 시간복잡도를 개선하기 위해, Softmax 함수의 근사치를 활용할 수 있다.
Negative Sampling 에서는 모든 Node가 아닌 $k$개의 Negative samples(Node $u$와 이웃하지 않는 Node)만을 사용해서 Softmax 함숫값을 근사한다.

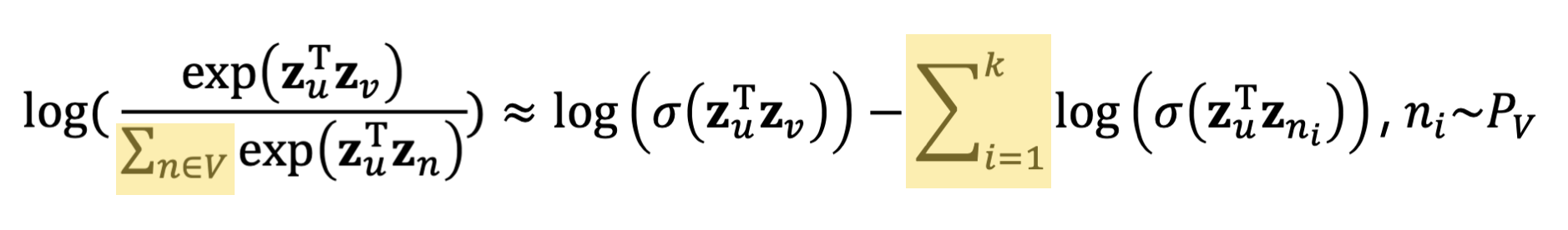
이때 $k$는 클수록 Robust Estimates를 가질 수 있으나 Negative Node들에 대한 Higher bias를 가질 수 있다는 점을 고려해야한다. 실질적으로는 5~20 사이의 값을 많이 선택한다고 한다.

이렇게 구해진 목적 함수 $\mathcal{L}$을 최소화하기 위해서 최적화 알고리즘 중 하나인 SGD(Stochastic Gradient Descent)를 사용할 수 있으며, 우리가 원하는 Embedding Vector들을 구할 수 있다.

4) Node2Vec

위에서 Negative Sampling 방식을 통해 계산 비용의 효율적으로 개선시킨 Random Walk 방식에서도 한계가 있다. 기존 방식에서는 균일한 확률로 고정된 길이(Unbiased & Fixed Length) 내에서 Random Walk를 진행하며 이웃 노드 $N_{R}(u)$를 구하고 있는데, 이는 노드 간의 유사성을 단일한 방식으로만 측정한다는 단점이 존재한다.

Node2Vec은 단일한 방식이 아닌 다양한 관점에서 이웃 노드 $N_{R}(u)$을 구함으로써 Embedding Vector에 더 많은 정보를 포함시키는 방식으로 기존 Random Walk 방식이 가지는 문제를 개선하고 있다.

Node2Vec은 아래의 2가지 개념을 활용한 Biased Random Walk 방식으로 이웃 노드를 구하고 있다.

① BFS/DFS를 활용한 그래프 탐색
Node2Vec은 아래 그림의 BFS를 활용하여 그래프의 Local(Micro-View) Network를, DFS를 활용해서 Global(Macro-View) Network를 탐색하는 방식이며 이를 통해 기존 이웃 노드가 가지는 의미를 확장시키고 있다.

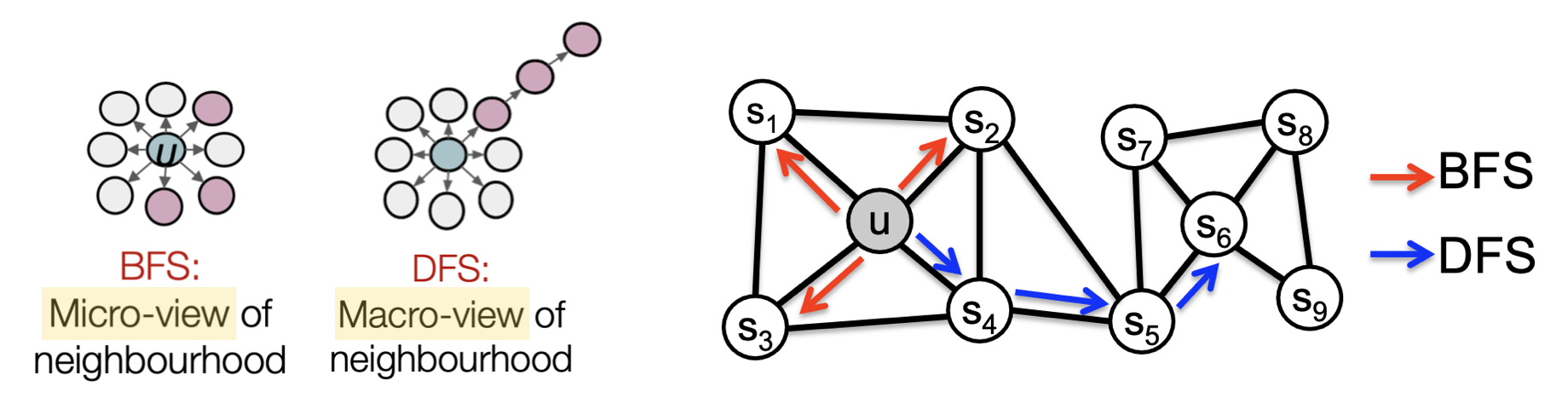
② Hyperparameter $p, q$
또한 Random Walk를 위해 2가지 Hyperparameter를 활용하고 있는데, 이전 노드로 이동할 확률을 의미하는 Return parameter $p$, BFS/DFS 탐색 방식의 비율을 의미하는 In-out parameter $q$(≈DFS, Walk Away)를 사용한다.

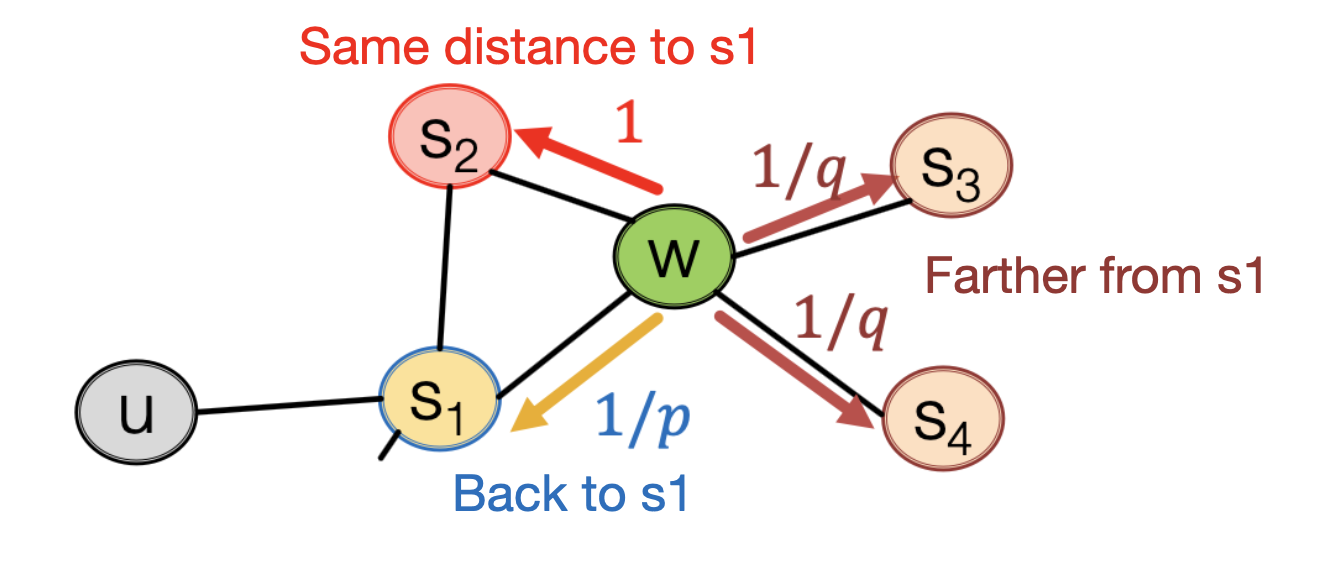
아래 그림과 같이 이전 노드가 $s_1$ 이고 현재 노드가 $W$ 일 때, 다음 이동할 노드를 선택하기 위해 $p,q$를 활용한다. 이동 가능한 모든 노드에 대해 가중치를 매긴 뒤에 이동할 노드를 선택하는 방식이며, 이 때 현재 노드와 이전 노드 모두 알고 있어야 하는 Biased 2nd-order random walks 방식이라고 할 수 있다.

• 노드 $s_1$에 대한 이동 가중치 : $1/ p$ , 이전에 있었던 노드
• 노드 $s_2$에 대한 이동 가중치 : $1$ , 이전 노드까지의 거리가 다음 노드도 동일한 경우
• 노드 $s_3,s_4$에 대한 이동 가중치 : $1/ q$ ,이전 노드로부터 더 멀어지는 노드

이러한 Node2Vec 방식은 선형 시간복잡도를 가지며, 병렬로 처리할 수 있어 효율적이다.
다만 Node2Vec이 모든 문제에 적합한 방식은 아니며, 적합한 Embedding Vector를 생성하기 위해서는 각각의 방식이 산출하고 있는 노드 유사도가 해결하고자 하는 문제에 적합한지를 고려하는 것이 우선되어야 한다.

---

3. Embedding Entire Graphs

앞서 노드를 Embedding하는 방안들을 소개하였는데, 실제로는 노드를 가지고 분류/예측하는 문제 뿐만 아니라 그래프 구조 자체를 분류/예측하는 문제도 존재한다. 예를 들어 특정한 분자 구조가 유독성을 갖는지 분류하는 문제나, 그래프 구조 자체에 대한 이상 여부를 분류하는 문제 등이 있다.

따라서 아래 본문에서는 그래프 전체를 Embedding 하는 방안들에 대해 소개하고자 한다.

1) Aggregation

가장 간단한 방법으로 그래프 내에 있는 모든 Node의 Embedding Vector를 더하거나 평균을 구해 이를 그래프의 Embedding Vector로 사용하는 방안이다.

2) Virtual node

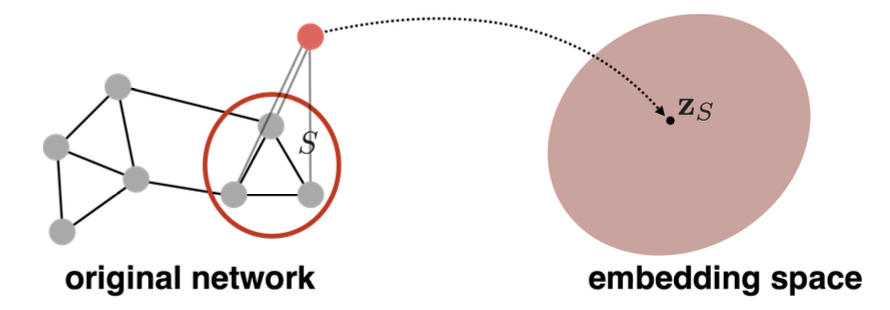
2번째로, 그래프를 대표하는 가상의 노드를 생성하여 이에 대한 Embedding vector를 사용하는 방식이다.

구하고자 하는 그래프(또는 Sub 그래프)와 연결되는 가상 노드(Virtual Node)를 만들고, 기존의 방식으로 해당 노드에 대한 Embedding Vector를 만드는 방식이다.

3) Anonymous walk embeddings

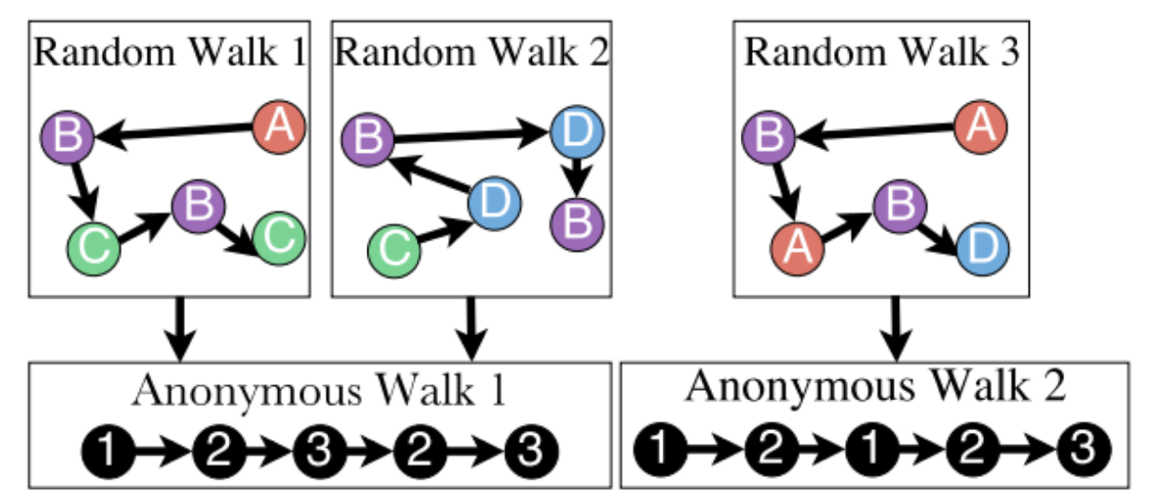
마지막으로 Anonymous walk embeddings은 이름에서도 알 수 있듯이 기존 Random walk 방식을 변형하여 사용하는 방식이다. 이는 각각의 노드의 특성을 고려하지 않고 단순히 방문한 순서에 따라 Index를 부여하여 노드를 구분함으로써 그래프의 구조에 집중하는 방안이다.

아래 그림의 예시처럼, Random Walk 방식에서는 A-B-C-B-C, C-D-B-D-B로 구분되던 것이 Anonymous Walk 방식에서는 1-2-3-2-3으로 동일한 Walk로 간주된다.

이때 Anonymous Walk의 Step이 늘어날수록 Walk 경우의 수는 지수적으로 증가하는데,
3개의 Step을 가질 때 Walk 경우의 수는 5가지(111, 112, 121, 122, 123)이지만 12개의 Step일 때는 경우의 수가 무려 4백만개이다.

① Simple Approches

Anonymous walk를 사용해서 그래프의 Embedding Vector를 구하는 간단한 접근 방안으로, 그래프에서 내에서 Anonymous walk $w_i$와 빈도를 구하고 이를 Vector로 사용할 수 있다.

이 때 walk의 경우의 수는 Vector의 차원이 되고, 빈도수는 Vector 값이 된다.

그런데 적절하게 walk의 경우의 수와 빈도를 구하기 위해서 몇번의 Anonymous walk를 수행해야 될까?
이를 판단하기 위해 아래 수식을 활용할 수 있다. 적절한 Anonymous walk의 수 $m$을 구하기 위한 수식이며, 이때 $\eta$는 Anonymous walk의 경우의 수이고 $\varepsilon , \delta$ 는 각각 최대 허용 오차와 1-신뢰 수준을 의미한다.

② Learn walk embeddings

Anonymous walk에 대한 Embedding Vector를 앞서 언급한 것과 같이 단순히 발생 횟수를 사용하는 대신 학습을 통해 구할 수도 있다.

각각의 $w_t(z_t)$를 구하기 위해서, 주변의 Anonymous walk $w_{t-\Delta}\cdots w_{t+\Delta}(z_{t-\Delta}\cdots z_{t+\Delta})$와 전체 그래프 $Z_G$ 를 이용하여 예측하도록 학습하며 이에 대한 목적 함수는 아래와 같다.

$w_{t-\Delta}, \;\ldots, \;w_{t+\Delta}$는 학습을 통해 구해지는 $z_{t-\Delta}\cdots z_{t+\Delta}$를 이용하며, 아래의 식을 참고하자.

1) Softmax 함수이며, 모든 walk의 경우의 수 또는 Negative Sample만을 사용할 수도 있다.

2) Linear Layer($b, U=$ 학습 파라미터)를 의미하며,
$\quad\text{cat}()$은 $z_i$의 평균과 $z_G$의 Concatenate를 의미한다.

$\begin{aligned} 1)\quad & P\left(w_t \mid\left\{w_{t-\Delta}, \ldots, w_{t+\Delta}, z_G\right\}\right)=\frac{\exp \left(y\left(w_t\right)\right)}{\sum_{i=1}^\eta \exp \left(y\left(w_i\right)\right)} \\ 2)\quad & y\left(w_t\right)=b+U \cdot\left(\operatorname{cat}\left(\frac{1}{2 \Delta} \sum_{i=-\Delta}^{\Delta} z_i, z_G\right)\right)\end{aligned}$

Learn walk embedding에서는 먼저 (1)각각의 노드 $u$로부터 길이 $l$을 갖는 Random walk $T$번을 수행하고, (2)해당 값과 예측된 값의 차이를 경사하강법을 통해 파라미터를 업데이트하는 과정을 반복하여 $z_G$를 최적화한다.

---

4. How to use embeddings

앞서 언급한 방법을 통해 구해진 Embedding vector $z_i$는 아래와 같이 다양한 Task에 활용될 수 있다.

• Clustering and Community detection : 군집의 중심 Point $\Rightarrow z_i$
• Node classification : Label 예측 $\Rightarrow z_i$
• Link prediction : 2개 Node 사이의 Edge 예측 $\Rightarrow z_i, z_j$
• Graph classification : Label 예측 $\Rightarrow z_G$