이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.
이번 글에서는 Graph를 구조를 Matrix(행렬)을 통해 다루는 방안에 대해 소개하려고 한다.
먼저 Node Importance를 구하기 위해 Random walk를 활용한 PageRank, Node Embedding 까지 활용하는 Maxtrix factorization 등에 대한 방법을 소개하려고 한다.
Overview
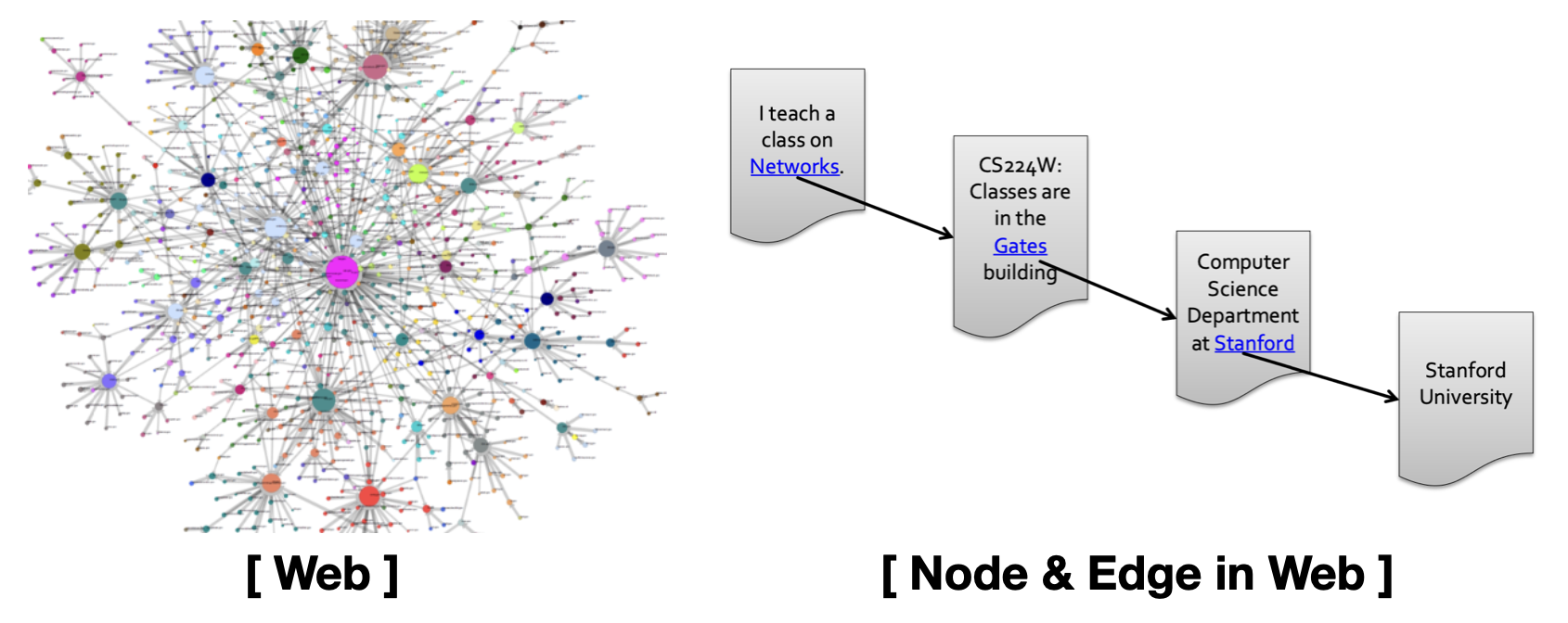
그래프 구조를 활용한 여러가지 사례 중에, Web을 그래프 구조 나타내는 사례를 살펴보자.
Web에 존재하는 각각의 Web page를 하나의 Node라고 볼 수 있고, Web page간의 Hyperlink는 하나의 Edge라고 볼 수 있다.
아래 우측 그림을 보면, 1개의 Node가 각각의 Web page라고 했을 때 다른 Web page를 참조하는 Hyperlink를 통해서 관계를 맺고 이를 Edge라고 할 수 있다. 이 때 Edge는 방향성을 가지기 때문에 Web은 Directed Graph 구조라고 말할 수 있다.
그런데 실제 Web page가 가지는 중요도는 모두 다를 것이다.
모두가 이용하는 네이버와 현재 이 글의 중요성이 같다고 말할 수 있을까?
따라서 Edge(Link)를 고려해서 각 Node(Web page) 중요도를 계산하고 순위를 매기는 Link Analysis approches 가 있으며 여기에 대한 방법들을 다뤄보려고 한다.
PageRank
가장 간단한 접근 방법으로, Web page가 가지는 Link의 개수를 통해 중요도를 계산하는 방식이다. Link에는 In-Link, Out-Link가 있는데 여기서는 해당 Web Page를 가리키는 In-Link의 개수만을 고려한다.
1️⃣ PageRank 수식
구체적인 계산 방법은 아래 그림과 수식을 보면 알 수 있는데,
중요도가 높은 Page로부터 Link를 받게 되면, 해당 Page도 이에 비례하여 더 높은 중요도를 가지게 된다.
Page 가 중요도 를 가지고 Out-Link(Out-degree) 를 가지면, 이때 각각의 Link는 의 중요도를 가지게 된다. 또 다른 Page 의 중요도는 In-Link의 중요도를 모두 합한 값을 통해 계산할 수 있다.
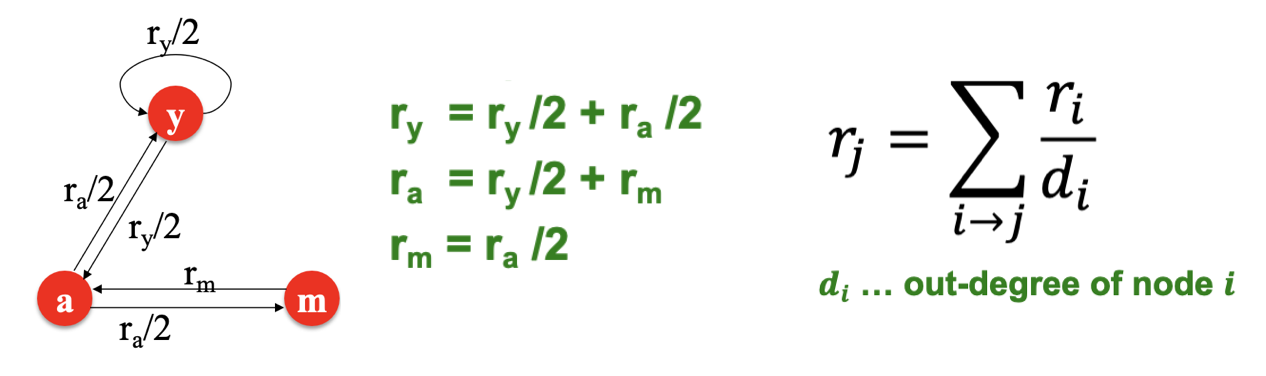
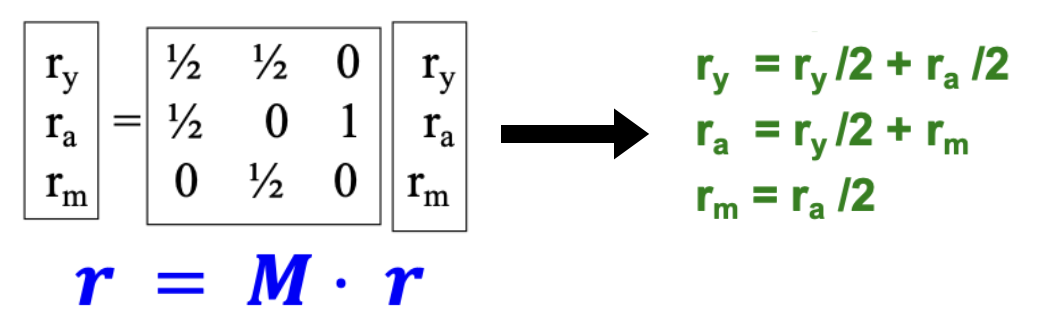
위의 식을 행렬(Link[Edge] 가중치)과 벡터(Page[Node] 중요도) 간의 곱셈 형태로도 표현할 수 있다.
먼저 행렬 은 Link 개수에 반비례하는 가중치로써, 특정 열벡터(Column vector, 특정 Page가 가지는 Out-Link의 가중치)의 합이 1을 가지는 Stochastic adjacency matrix이다.
다음 벡터 은 각 Page의 중요도로써, 이 또한 모든 벡터값(중요도)의 합이 1을 가진다.
이렇게 행렬식을 사용하여 앞에서의 식과 동일한 형태로 나타낼 수 있고, 이를 Flow Equations 이라 한다.
각 Page의 중요도에 대한 수식을 이렇게 세웠고 각각의 중요도(해)를 구하기 위해 가우스 소거법을 적용해보면, 순환(예 : )이 포함되어 있기 때문에 쉽게 구해지지 않기 때문에 Random Walk와 같은 방식을 활용할 수 있다.
2️⃣ PageRank with Random walk
Page Rank를 Random Walk 관점에서 생각해보자.
현재 ① Page 에서 임의의 Out-Link를 따라 이동했을때 도착하는 Page 를 기록하는 과정을 ② 무한히 반복한다면, 각 Page에 도착할 확률 를 알 수 있다.
이를 반복할수록 아래 수식과 같이 벡터값이 수렴하여 변동성 없는 stationary distribution 값을 가지게 되고, 이를 각 Page에 대한 중요도를 의미하는 로써 활용할 수 있다.
이러한 방식을 Power Iteration 이라고 말한다.
Power Iteration
Page Rank를 계산하기 위해 Random Walk를 활용하는 Power Iteration이 실제로 어떻게 동작하는지, 문제점은 없는지 자세히 살펴보자.
1️⃣ 동작 및 예시
Power Iteration의 동작 순서를 살펴보면 아래와 같다.
① 모든 Page의 중요도 초기화
② 현재 Page 중요도를 사용하여 Flow Equation 계산 및 중요도 업데이트
③ 업데이트 전/후 Page 중요도가 오차값보다 낮으면 중단
- 이때 오차 계산은 L1 norm 이외에 다른 방식도 사용 가능하다. (ex. L2 norm)
아래는 Power Iteration에 대한 예시이다.
Flow Equation에 의해 중요도가 계속 업데이트 되고 특정 값으로 수렴되는 것을 알 수 있다.

2️⃣ 문제점
위의 예시와 같이 적절한 중요도를 찾아낸다면 좋겠지만, 현재의 Power Iteration 방식은 몇몇 사례에서 제대로 동작하지 않고 특정 Page(Node)에 편향되거나 중요도가 전체 Web(Graph)내에서 순환되지 않는 경우 등 문제점이 있어, 이를 보완할 수 있는 방식이 추가로 필요하다.
① Spider traps
Spider traps은 Out-Link가 특정 Page 그룹 내에서만 존재하는 경우에 발생하는 문제이다.
이러한 경우 In-Link를 통해 다른 Page로부터 유입된 중요도가 다시 나가지 못하기 때문에 해당 그룹에 중요도가 편향되고, 이 외 Page의 중요도는 제대로 계산되지 않는 문제가 있다.
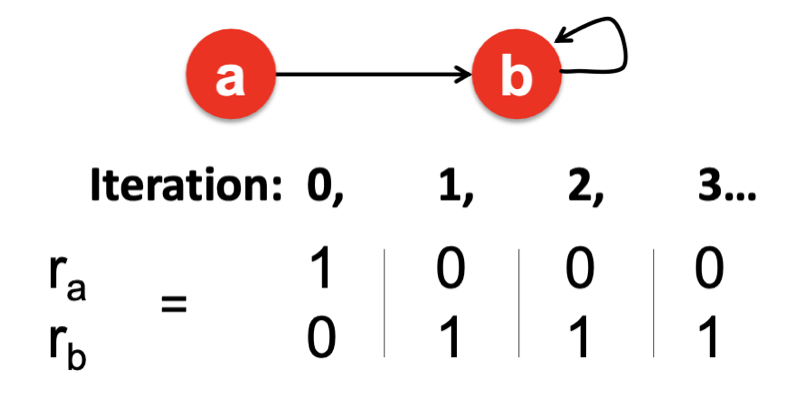
이때 수학적인 관점에서 문제가 있는 것은 아니지만, 특정 그룹 외 Page의 중요도가 굉장히 낮아지기 때문에 우리가 원하는 방향으로 수렴한다고 볼 수 없고 보완이 필요하다.
② Dead ends
Dead ends는 In-Link는 있지만 Out-Link가 없는 Page(Node)가 존재할 때 발생하는 문제이다.
Out-Link가 없는 Page에 유입되는 중요도는 다른 Page로 전달되지 못하고, 아래 그림과 같이 중요도가 유실된다는 문제점이 있다.
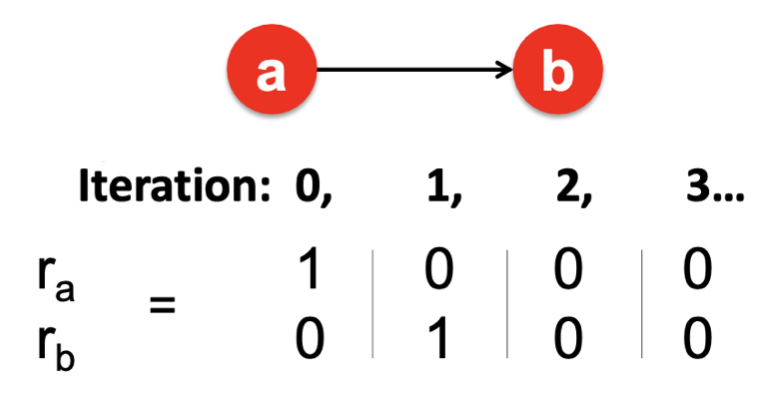
이때 수학적으로 접근했을때도, 행렬 의 열벡터 합이 1이 되지 않기 때문에 초기의 가정이 어긋나게 되기 때문에 해결해야하는 문제 중 하나이다.
3️⃣ 해결방안
앞서 언급했던 문제점들에 대해 어떻게 해결할 수 있을지 살펴보자.
① Spider traps
먼저 Spider traps의 경우 중요도가 특정 그룹 내에서만 순환되지 않도록, 정해진 경로 내의 Page가 아니라 랜덤으로 다른 Page로 이동할 수 있도록 하는 방안이 있다.
확률을 나타내는 를 사용하여, 특정 그룹 외의 Page로도 이동할 수 있게끔하여 문제를 해결하는 방안이다.
- with Probability : 정해진 경로 내의 Page로 이동
- with Probability : 정해진 경로 외의 다른 Page로 이동
② Dead ends
Dead end, 즉 Out-Link가 없는 Page에 대해서는 열벡터의 값을 0으로 두는 것이 아니라, 합이 1이 되도록 모든 원소에 임의의 값을 부여하는 방안이다. 이는 Graph에 존재하는 모든 Page에 이동할 수 있게끔 하여 중요도가 유실되지 않으면서 특정 Page에 영향을 미치지 않게끔 보완한 방안이다.
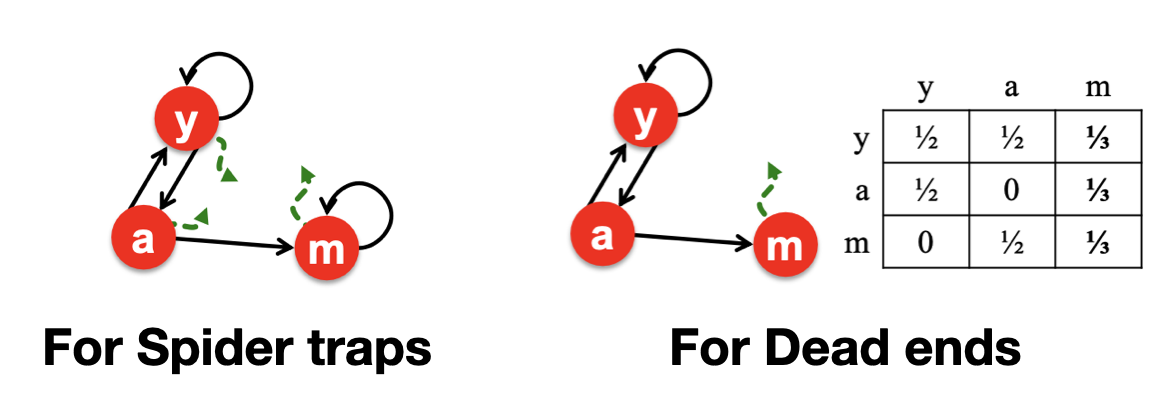
4️⃣ The Google Matrix
Google에서는 Spider traps과 Dead Ends 문제를 해결하기 위해 위의 2가지 해결방안을 종합한 Google Matrix를 제안하였다. 해결하는 방안은 앞서 언급한 바와 동일하며, 이를 아래와 같이 수식에 반영하였다.
PageRank Equation
The Google Matrix G
기존에는 행렬 을 활용한 Flow Equation을 통해 중요도를 업데이트하였으나,
여기에서는 2가지 보완점을 반영한 확률 인접 행렬 를 이용한 Flow Equation 을 사용할 수 있다.
추가로 는 0.8 또는 0.9를 주로 사용하며, 이 때 평균적으로 4~5번 업데이트 중 Random 이동이 1번 일어남을 의미한다. 추가로 아래는 행렬 가 계산되는 과정을 나타낸다.
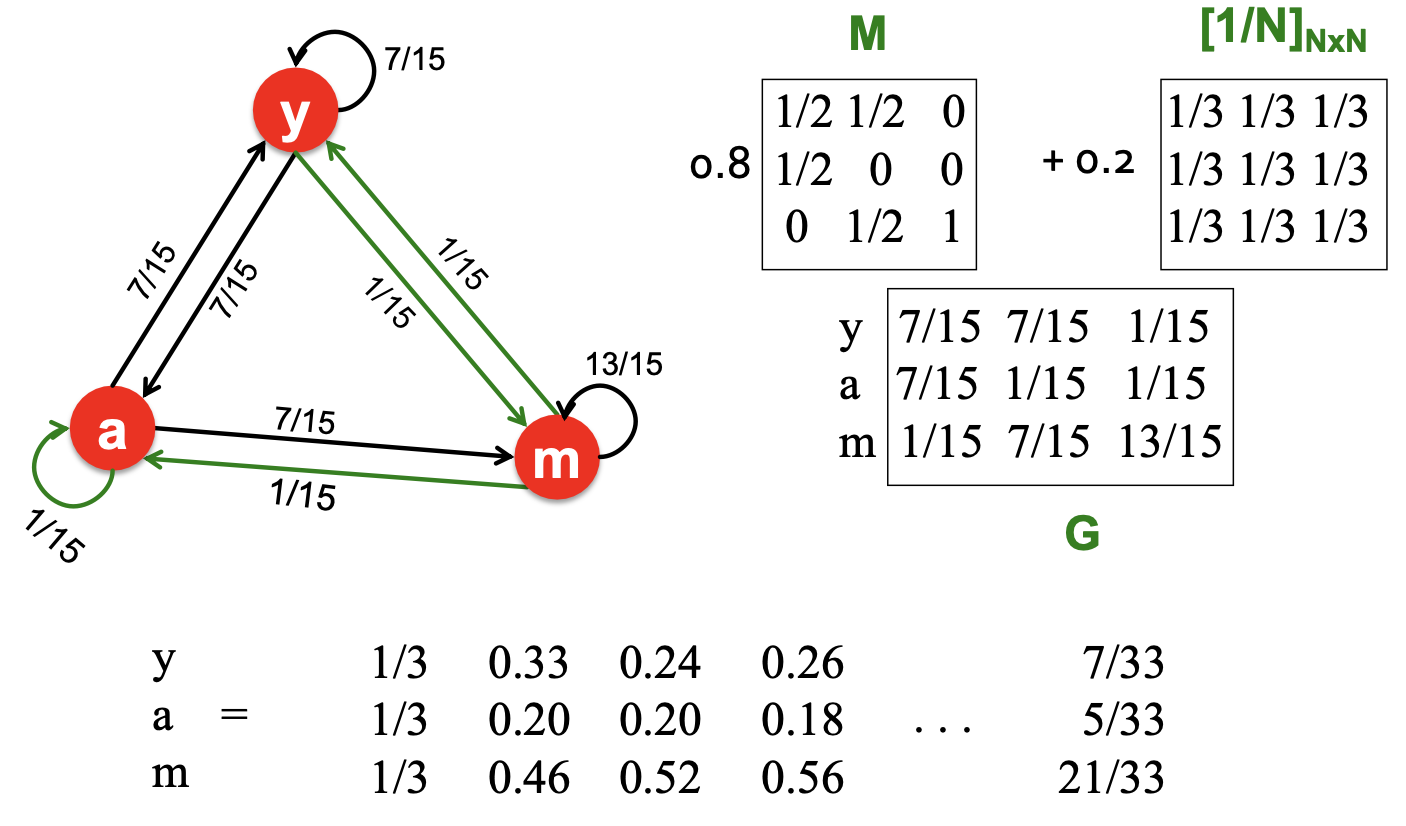
PageRank Variants
특정 Task에서 기존보다 효율적인 PageRank를 수행하기 위해서, 다른 제약 조건을 추가하고 변형시킨 PageRank Variant 들에 대해서 알아보자.
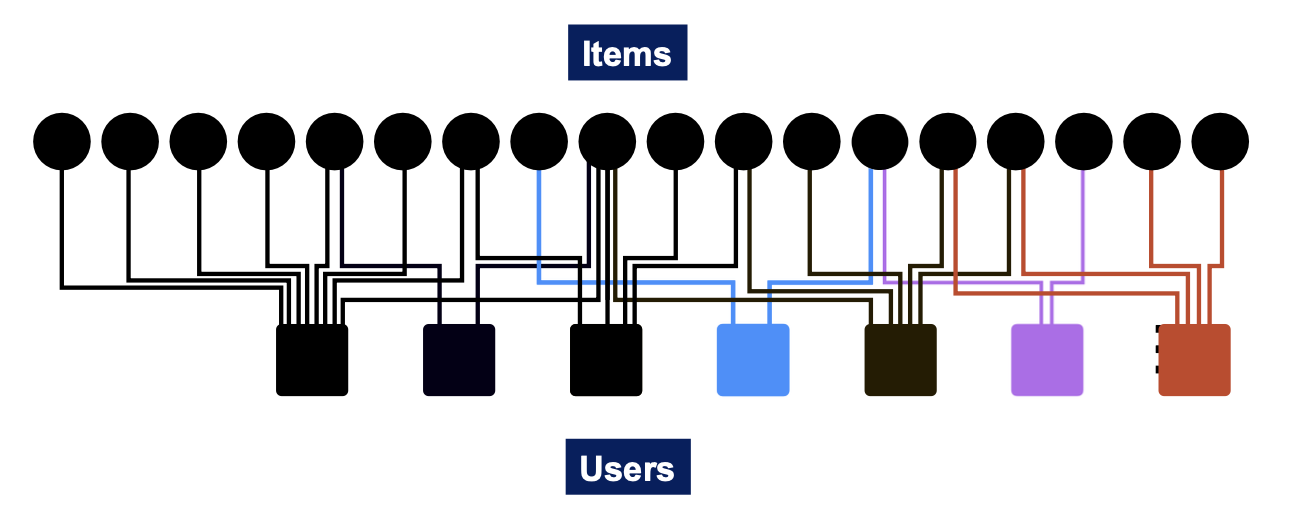
추천 시스템을 예로 들자면, 먼저 물품(Item)과 사용자(User)의 관계를 이분 그래프(Bipartite graph) 형태로 표현할 수 있다. 일반적으로 추천 시스템에서는 사용자 ❶과 ❷가 동일한 물품 를 구매했다면 사용자 ❶에게는 ❷가 구매했었던 다른 물품 을 보여주는 방식으로 새로운 물품을 추천한다. 이는 사용자의 구매 이력을 바탕으로 물품 간의 유사도를 측정하는 방식이라고 말할 수 있다.
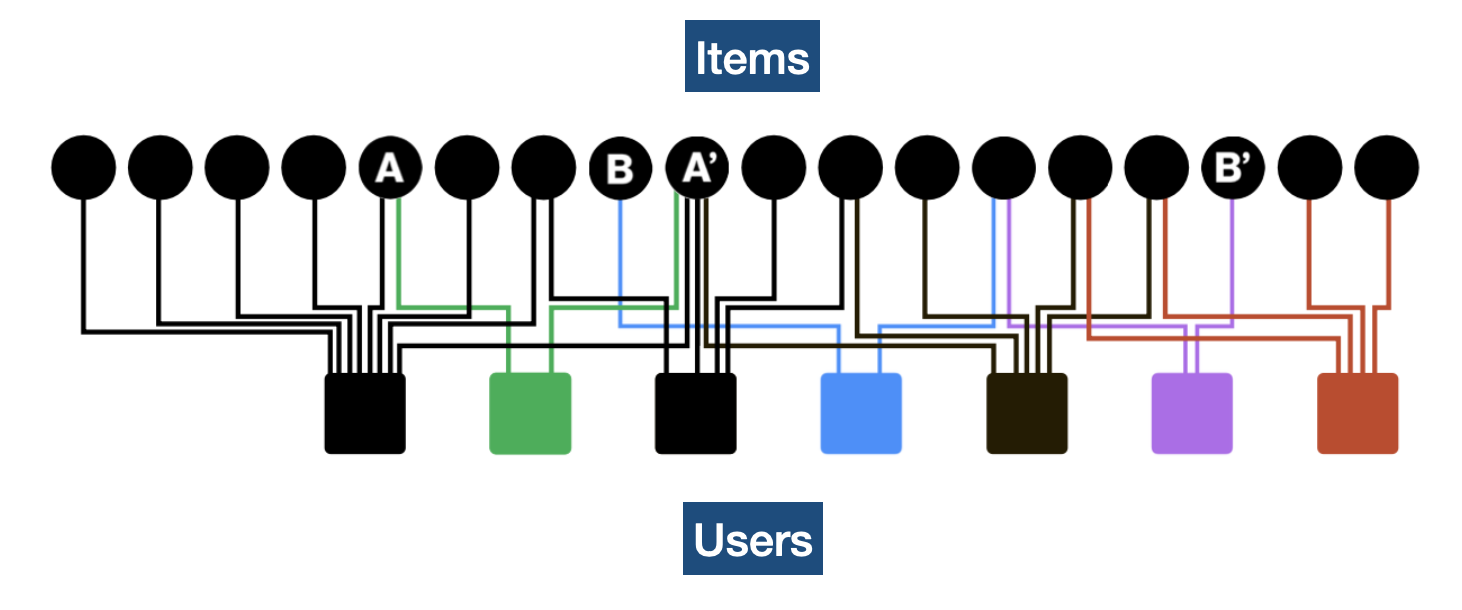
다만 아래와 같이 2명의 사용자가 동일한 물품을 구매하는 경우, 이웃이 1명이 있는 경우만 해도 굉장히 다양한 케이스가 있다는 것을 알 수 있다. 아래의 예시와 같이 2개 물품을 구매했는데 1개 물품이 겹치는 경우와, N개 물품을 구매했는데 1개 물품이 겹치는 경우가 새로운 물품을 추천할때 같은 우선순위라고 말할 순 없을 것이다. 즉 이러한 케이스들 간의 우선순위를 정하기 위해서는 앞서 언급했던 유사도의 수치화가 필요하다.
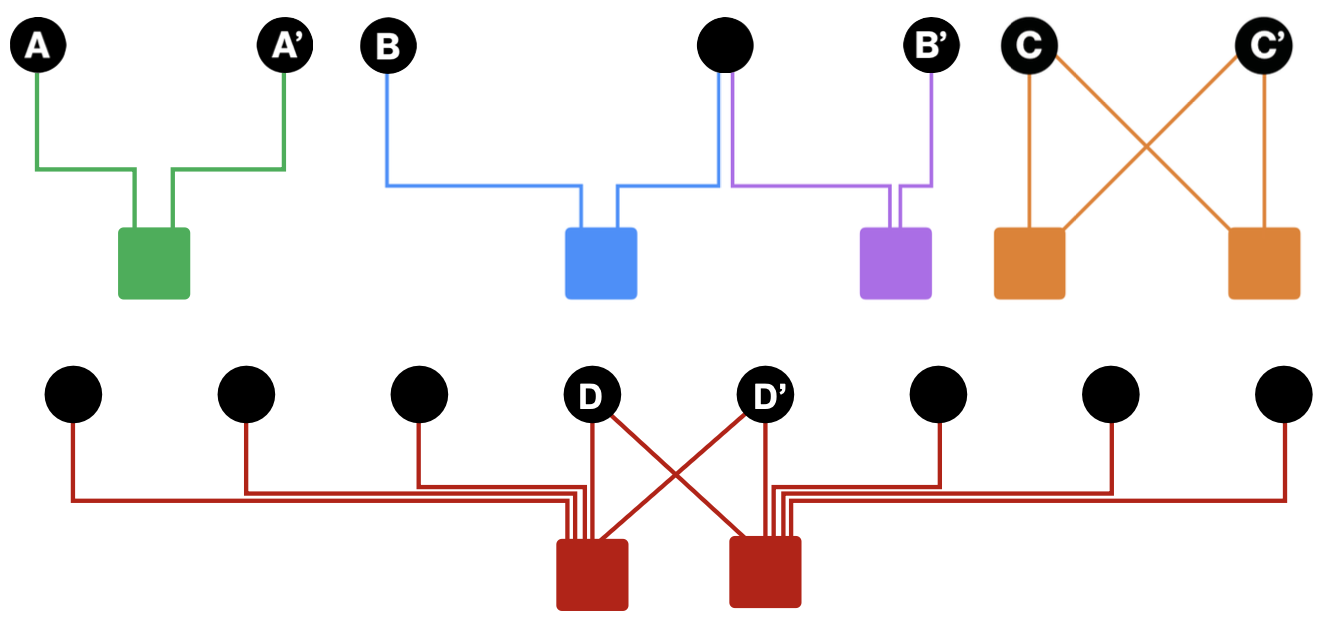
1️⃣ Personalized PageRank
유사도의 수치화를 위해서 PageRank에 제약 조건을 추가한 방식을 사용하는데, Personalized PageRank(이하 PPR)이라고 불리는 이 방식은 기존 PageRank에서 Random으로 Graph 내의 임의의 Node로 이동하던 것을, Graph 내의 Subset(특정 Node들의 집합)에 해당하는 임의의 Node로 이동하는 방식이다.
사용자가 공통으로 구매한 물품 에서 PPR 알고리즘을 수행하면, 사전에 정의한 해당 물품과 관련된 Node들로만 이동하게 되고 물품 와 다른 물품들간의 유사도를 구할 수 있다.
이를 Adjacency Matrix 표현하자면, 기존 Page Rank에서는 열벡터를 기준으로 동일한 값(ex. 1/N)을 부여해줬고, PPR에서는 Subset에 해당하는 Node들에 대해서만 특정 값을 부여하고 나머지는 0으로 초기화한다. 이때 아래 그림과 같이 Node별로 다른 값을 부여할 수 있다.
2️⃣ Random Walk with restart
앞서 언급한 PPR에 1가지 제약 조건을 추가한 방식이 있는데, Random으로 이동할 수 있는 대상을 시작 Node 1개로 한정시켜서, Random으로 시작점에서부터 다시 시작하게 하는 방식이다.
아래는 Pseudo Code로 작성된 알고리즘의 예시인데, QUERY_NODES는 Random으로 이동할 수 있는 대상을 의미하며 좌측과 같이 시작 Node 만 들어있는 것을 볼 수 있다.
1번의 Random Walk가 진행되는 과정을 살펴보면,
① 물품 → 사용자 → 물품 로 이동하여
② 물품 의 방문 횟수를 체크하고
③ 만약 확률 에 해당하는 경우 시작점에서부터 다시 진행하는 Restart를 수행한다.
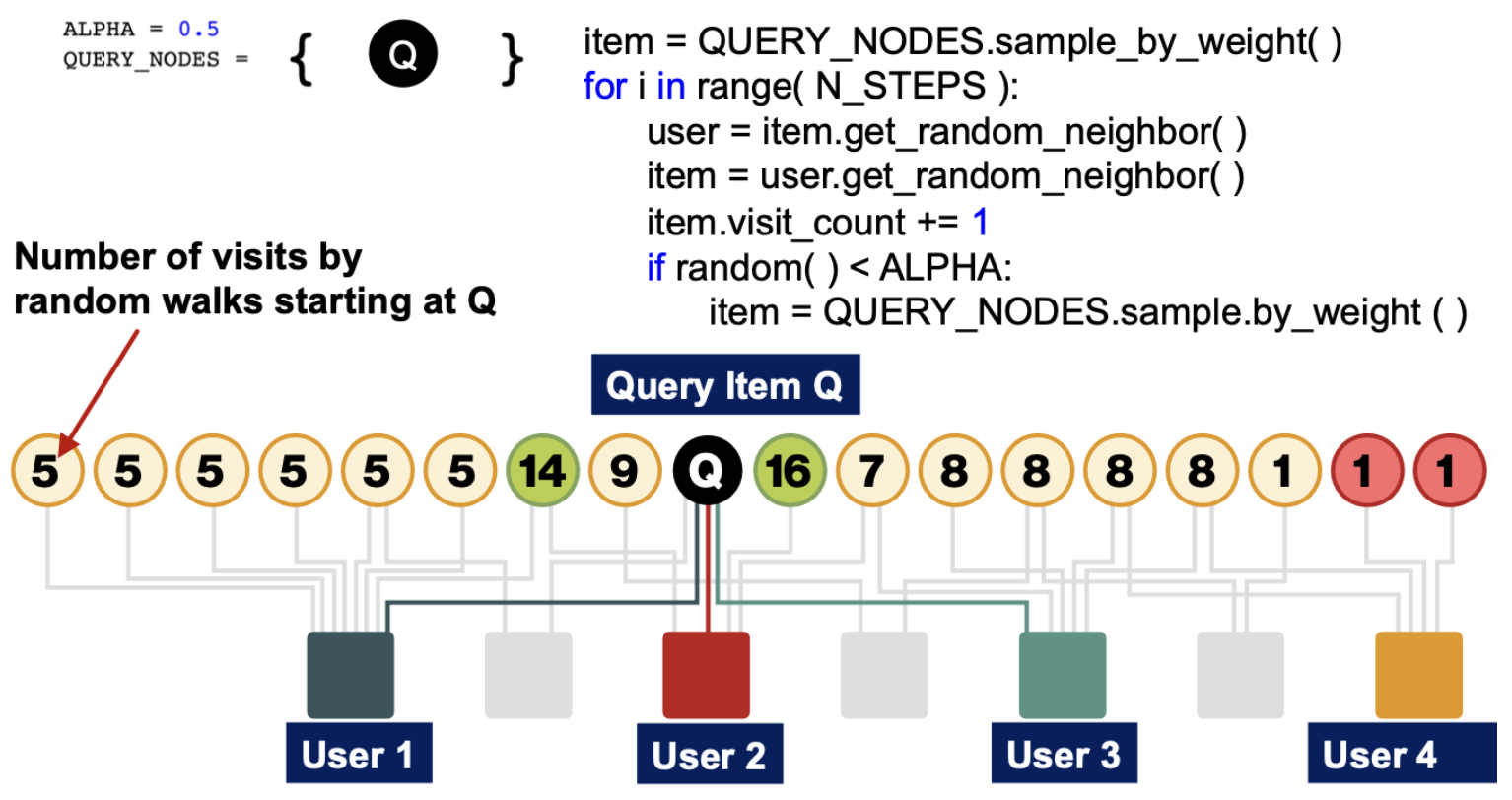
여기에서도 Adjacency Matrix 표현해보면, 시작 Node를 제외한 나머지는 0으로 초기화함을 알 수 있다.
장점
이러한 Restart 방식을 통해 다양한 케이스를 고려한 특정 Node와 다른 Node 간의 유사도를 구할 수 있다.
① 다중 연결 및 경로 (Multiple connections and paths)
② 단방향/양방향 연결 (Direct and indirect connnections)
③ Node별 Link의 개수 (Degree of the node)
Matrix Factorization
앞에서 다루었던 Random Walk 및 PageRank 모두 Graph 데이터를 Adjacency Matrix 형태로 표현하여 다루었는데, 이렇게 행렬을 사용하여 표현하면 각 Node를 고정된 크기의 Vector로 변환하는 Node Embedding 과정을 수학적으로 다룰 수 있다.
이전 글 Node Embeddings에서 다루었던 내용을 다시 복기해보면, 서로 연결된 Node Pair에 대해서는 Embedding vector 간의 내적 값을 최대화하는 방향으로 Embedding을 진행하였다.
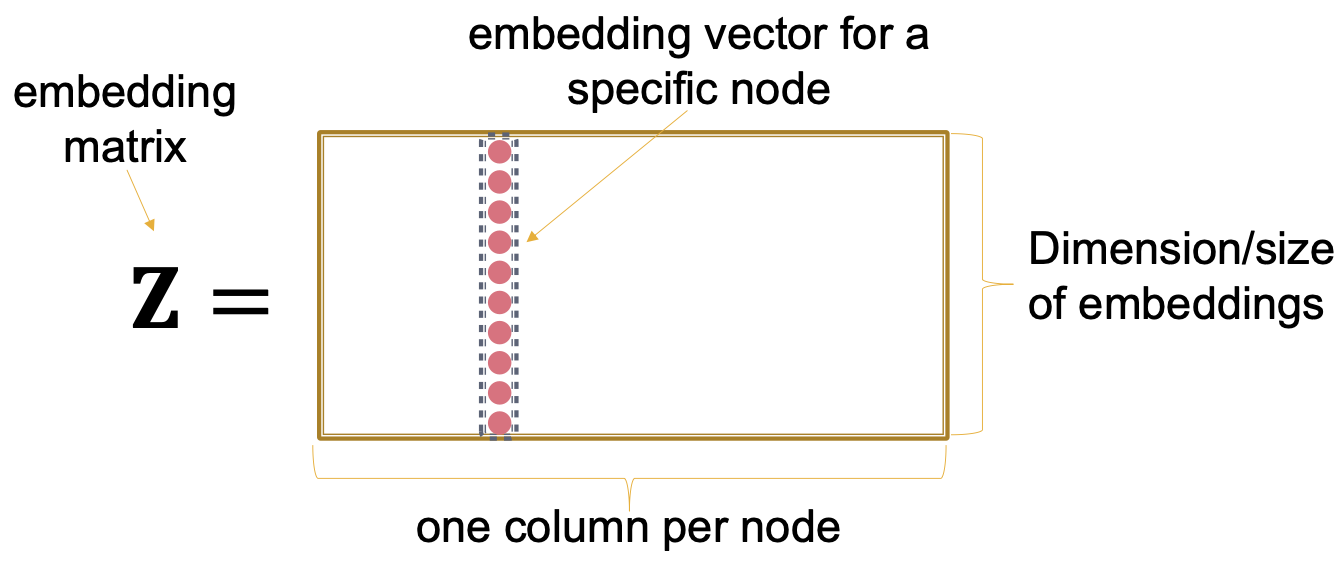
이를 확장시키면 Matrix 관점으로 확장시키면,
Graph Adjacency Matrix Embedding Matrix 으로 나타낼 수도 있다.
1️⃣ Matrix Factorization 최적화
다만 현실적으로 완벽하게 에 해당하는 를 구할 수 없기 때문에,
아래와 같은 최적화 문제를 해결하는 방식으로 를 구할 수 있다.
Random Walk 기반의 알고리즘인 Deep Walk, Node2Vec 모두 Matrix Factorization 형태로 표현할 수 있다. 아래 이미지의 수식은 Deep Walk에 대한 수식이고 여기에 Matrix Factorization 기반의 해석을 덧붙였다.
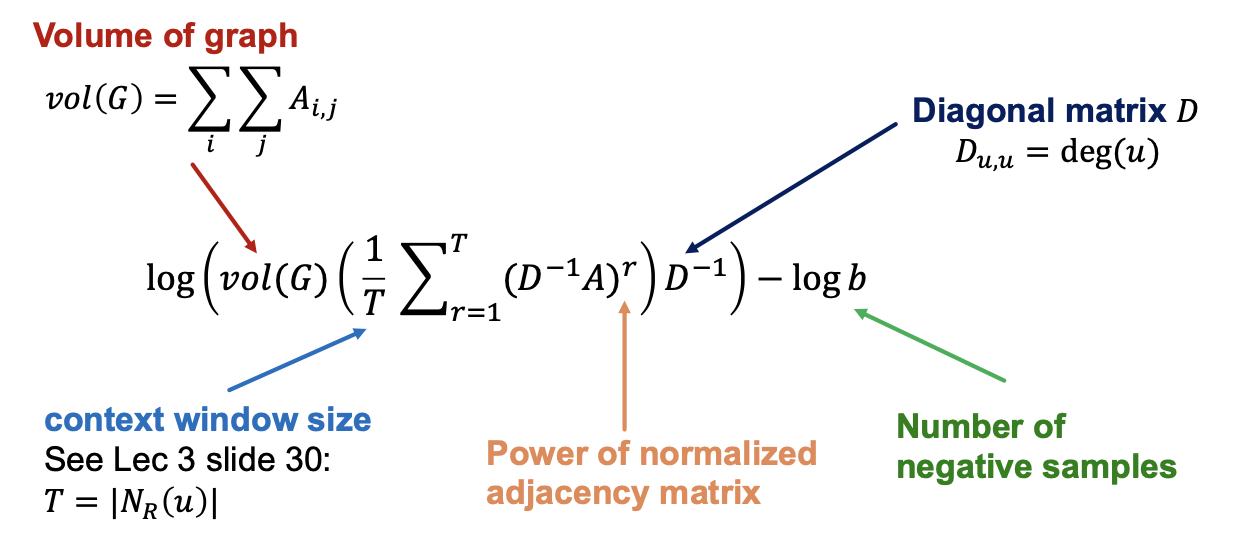
현재 Node Embedding 한계
Deep Walk와 같은 Node Embedding 방식들은 모두 Random Walk 기반의 방식이며, 이를 Matrix Factorization 방식으로 표현 가능함을 알 수 있었다. 다만 이러한 방식에는 존재하는 몇가지 한계에 대해서 알아보고, 다음 글에서는 어떻게 이런 문제점들을 해결할 수 있는지 알아보자.
① 새로운 Node에 대한 대응 어려움
Training Set에 없는 Node가 생성된다면, 이에 대한 Embedding Vector를 생성하기 위해서는 해당 Node를 포함해서 알고리즘을 다시 수행해야한다는 단점이 있다.
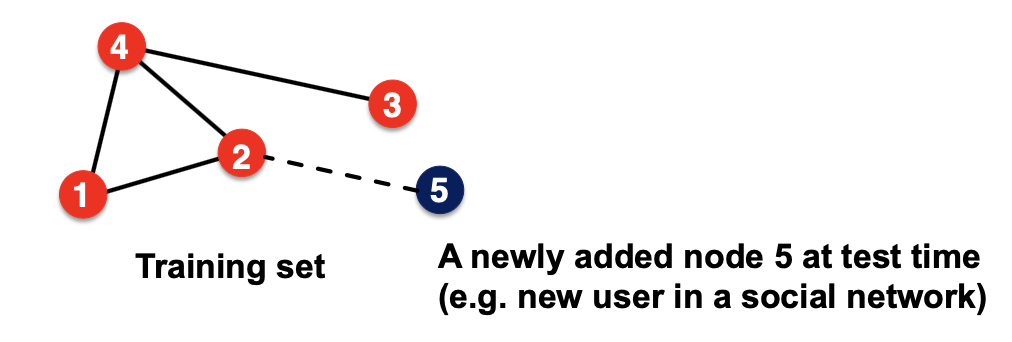
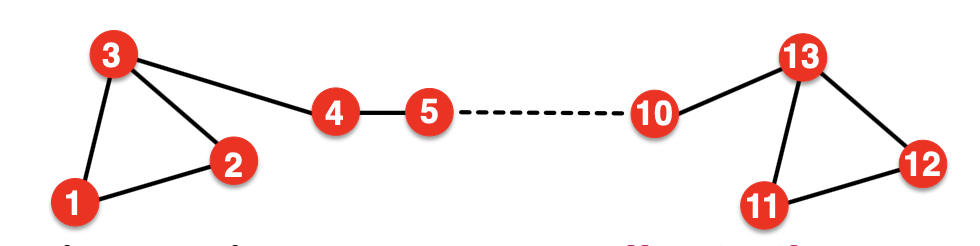
② 구조적 유사성 발견의 어려움
아래 그림에서는 1번 Node와 11번 Node는 구조적으로 유사한 위치(삼각형에서 동일한 위치 / Degree 2)이나, 실제 Embedding Vector는 다른 위치에 생성된다. Random Walk의 경우 인접한 Node 위주로 유사도를 측정하기 때문에 이러한 구조적 유사성(structurally similar)을 Embedding Vector에 포함시키기 어렵다는 단점이 있다.
③ Node/Edge/Graph Feature 활용 불가
마찬가지로 Random Walk의 방식에서는 연결된 Edge의 수로만 유사도를 측정하기 때문에, 이외의 다른 Feature 정보를 활용하기 어렵다.
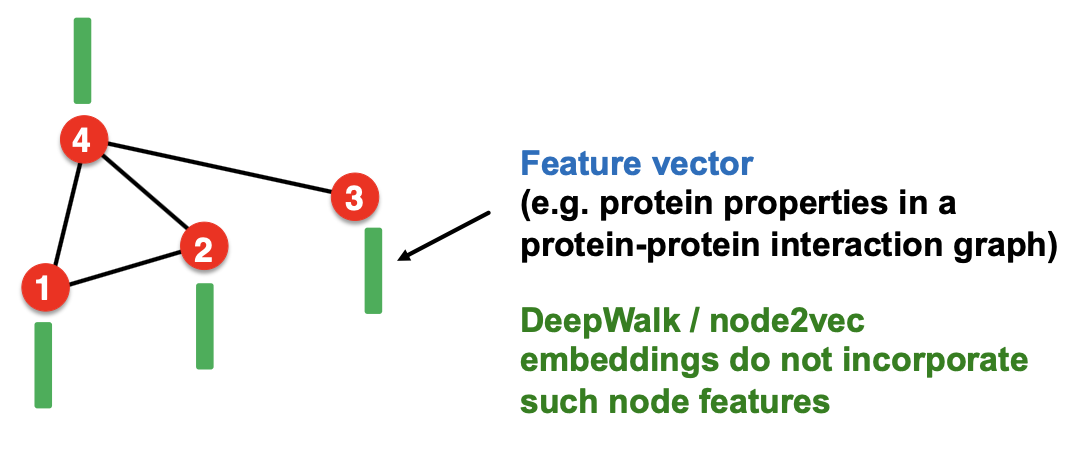
이러한 문제점들을 개선하기 위해 Deep Learning 기반의 Graph Neural Network이 활용되고 있으며, 다음 글에서는 여기에 대한 내용을 다뤄보고자 한다.