이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.
이번 글에서는 Graph 구조에서 Node Classcification을 어떻게 수행하는지, 여기에 가장 많이 활용되는 Message Passing 방식을 포함하여 다뤄보고자 한다.
Collective Classification
아래의 그림은 Graph 구조에서의 Node Classification의 한가지 사례로, Network(Graph)에서 일부는 Labeled Node이지만 Unlabeled Node인 다른 일부에 대해서 Node Classification (Semi-Supervised Learning)을 수행하는 경우이다.
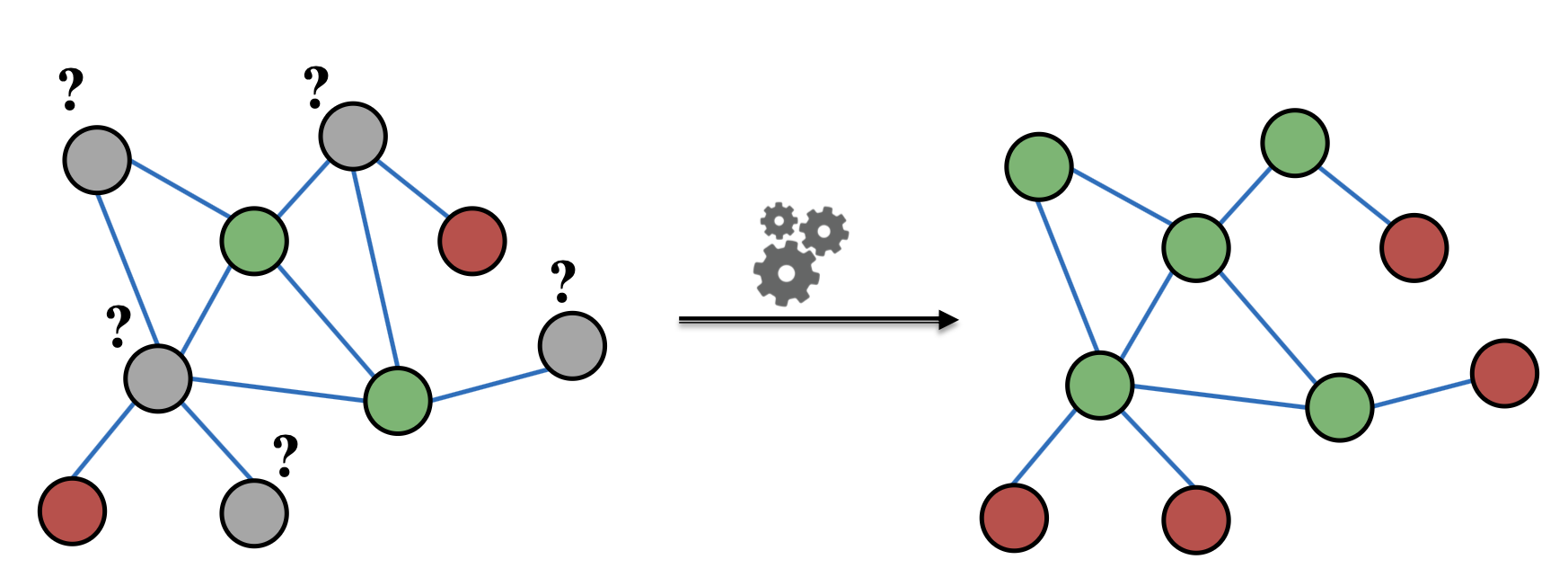
앞서 다뤘던 Node Embedding, Page Rank 모두 현재 Node와 이웃 Node 간의 관계를 활용하는 방식으로 Node Classification에서도 이웃 Node 간의 Correlation을 활용할 수 있으며 이를 Collective Classification 이라고 한다.
1️⃣ Correlations in Networks
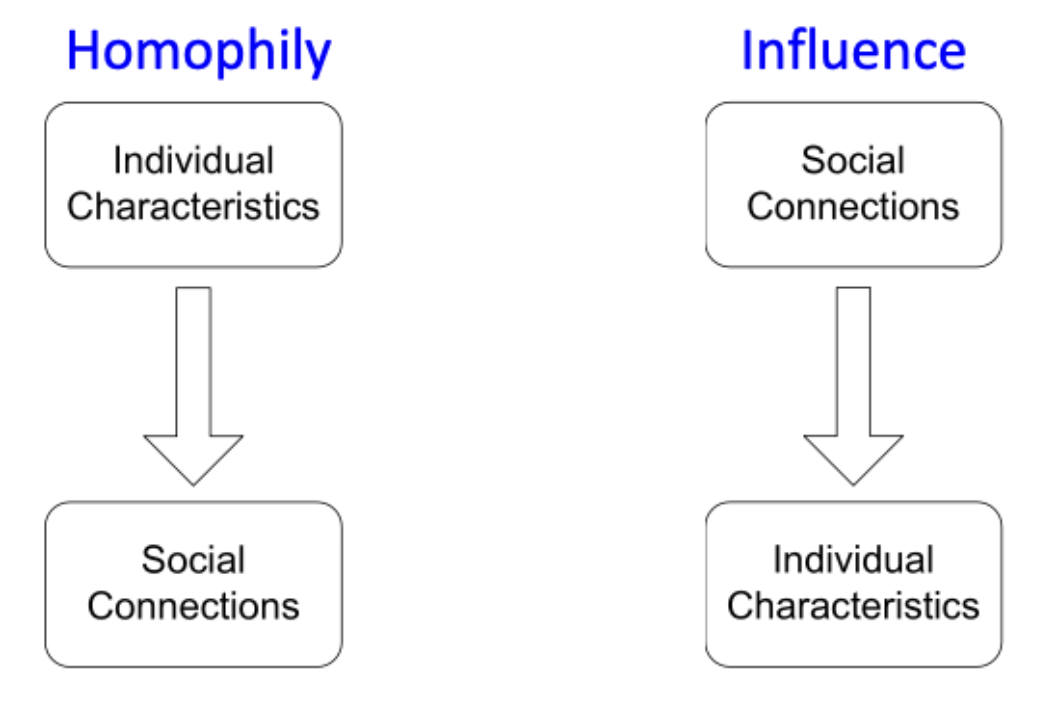
Collective Classification에서 활용되는 Correlation(상관관계)에는 크게 Homophily(동질성)과 Influence(영향력) 2가지 유형으로 구분할 수 있으며 각각 어떤 개념인지 살펴보자.
① Homophily
Homophily(동질성)은 유사한 Node들이 서로 연결될 가능성이 더 높은 경향을 가진다는 이론이며, 각 Node의 특성이 Network 내에서의 연결로 이어짐을 의미한다. 한가지 예로 우리가 같은 관심사를 가진 사람들끼리 친구가 되거나 마주칠(연결) 확률이 더 높다는 것을 말할 수 있으며, 이러한 Homophily는 다양한 분야(age, interests 등)에서 공통적으로 나타나는 현상이다.
② Influence
Influence(영향력)은 개별 Node의 특성이 다른 이웃 Node에 전파되어 영향을 미치게 된다는 이론이며, Network 내의 연결이 각 Node의 특성으로 이어짐을 의미한다. 예를 들자면 내가 친구에게 어떤 음악을 추천하고 친구가 그 음악을 좋아하게 되는 경우를 말할 수 있으며, 이러한 Influence는 Social Network에서 특히 많이 나타나는 현상이다.
2️⃣ Method
Collective Classification에서 사용되는 주요한 기법들로, 아래와 같은 특징이 존재한다.
- Relational Classification
: 이웃 Node의 Label만을 활용해서 이를 가중 평균하여 현재 Node Label을 갱신하는 방식 - Iterative Classification
: 이웃 Node의 Label과 Node 속성을 활용하는 분류기를 만들고 Node Label을 갱신하는 방식 - Loopy Belief Propagation
: Message Passing 기반의 확률적 추론으로, 방식과 달리 Homophily 속성에 의존적이지 않은 방식
Relational Classification
Relational Classification은 위에서 언급한 것과 같이 이웃 Node의 Label(Class)만을 활용해서 Node Classification을 하는 방식이다. 구조가 간단하여 구현이 쉽다는 장점이 있으나 각각의 Node가 가지는 속성은 활용하지 않고 알고리즘의 수렴이 보장되지 않는다라는 단점이 있다.
1️⃣ 수식 및 알고리즘
Relation Classification에서 알고리즘의 계산 순서를 살펴보면 아래와 같다.
① Initialization: Unlabeled Node의 을 0.5로 초기화한다.
은 Node 가 Class 에 속할 확률을 의미하며, Labeled Node를 제외한 모든 Unlabeled Node에 대해서 확률값을 0.5로 초기화한다.
② Update: Unlabeled Node의 확률값을 아래 수식을 통해 업데이트하고 수렴할때까지 반복한다.
아래 수식에서 는 Graph에 대한 인접 행렬을 의미하며, 이웃 Node의 확률값을 가중 평균하기 위해 Normalize 식(분모)이 추가되어있다. 만약 Edge에 가중치가 존재한다면 이웃 Node의 확률값이 각각 다른 비율로 반영되나 가중치가 없다면 동일하게 반영된다.
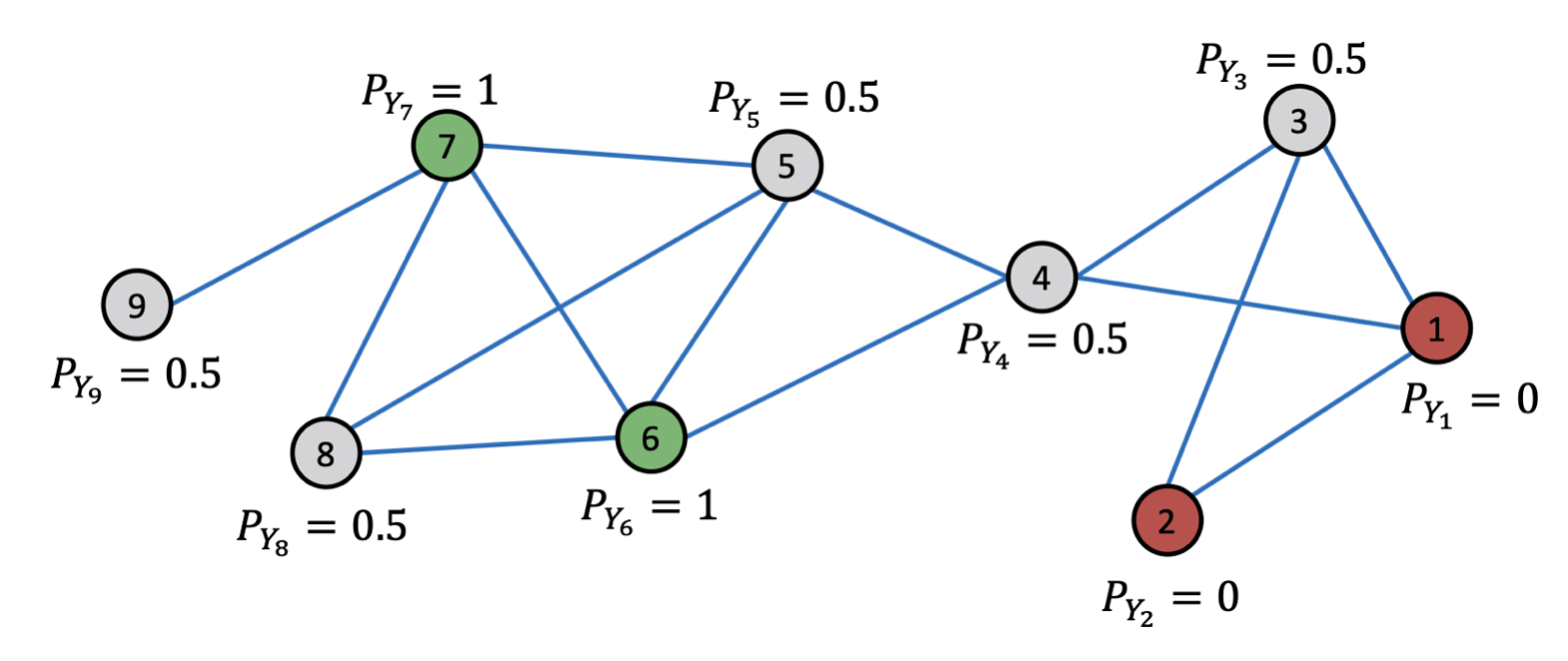
아래 그림에서 3번 Node의 경우, 연결된 1/2/4번 Node의 Class를 활용하여 3번 Node의 Class에 대한 확률 값을 업데이트한다.
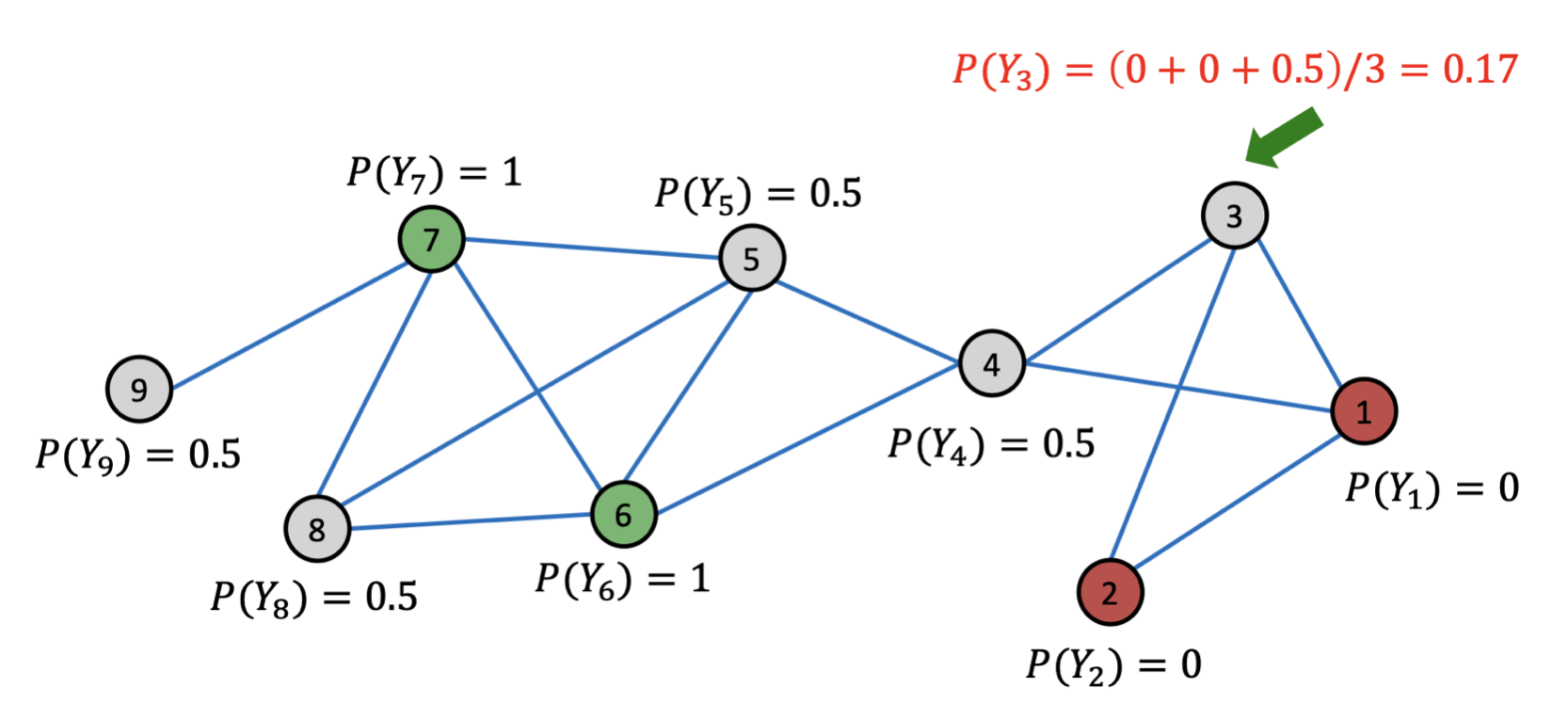
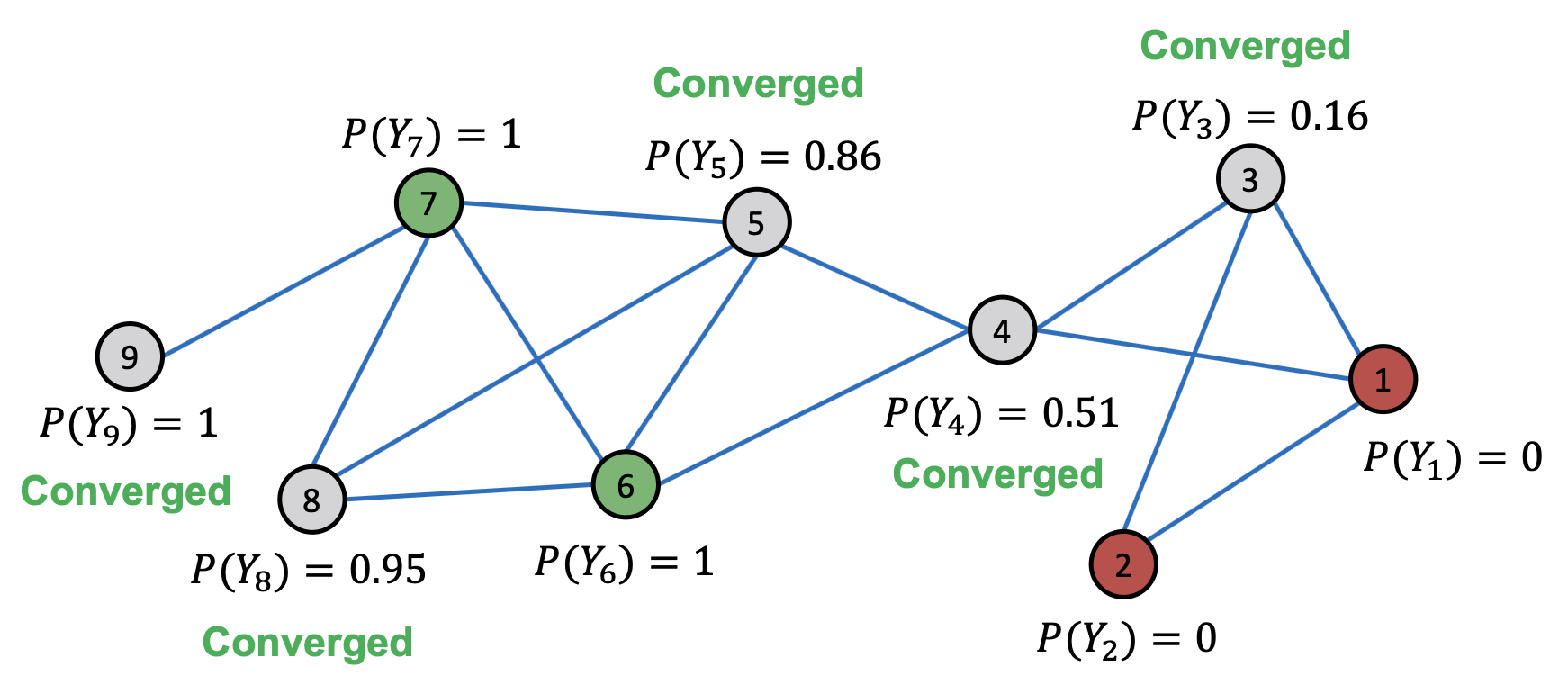
이러한 과정을 모든 Unlabeled Node에 대해 수행하고, 확률값이 수렴하게 되면(또는 최대 반복 횟수에 도달하면) 업데이트를 멈추고 확률값에 따라 Class를 구분할 수 있다. 아래 그림에서는 1/4/5/8번 Node의 Class=1() 이고, 3번 Node의 Class=0() 임을 알 수 있다.
Iterative Classification
Iterative Classification은 이웃 Node의 Class 정보만 활용하는게 아니라 Node의 속성 정보도 활용하여 Node Classification을 하는 방식이다. 이때 Classifier 2개를 사용한다.
각각의 Classifier는 아래와 같은 역할을 한다.
- : Node 가 가지는 속성 을 사용하여 Class 예측
- : Node 가 가지는 속성 와 이웃 Node의 Class에 대한 요약 정보 를 사용하여 Class 예측
- : Most common label in , Histogram of the number of each label in ...
1️⃣ 수식 및 알고리즘
하나의 예시를 통해 알고리즘이 동작하는 방식을 살펴보자.
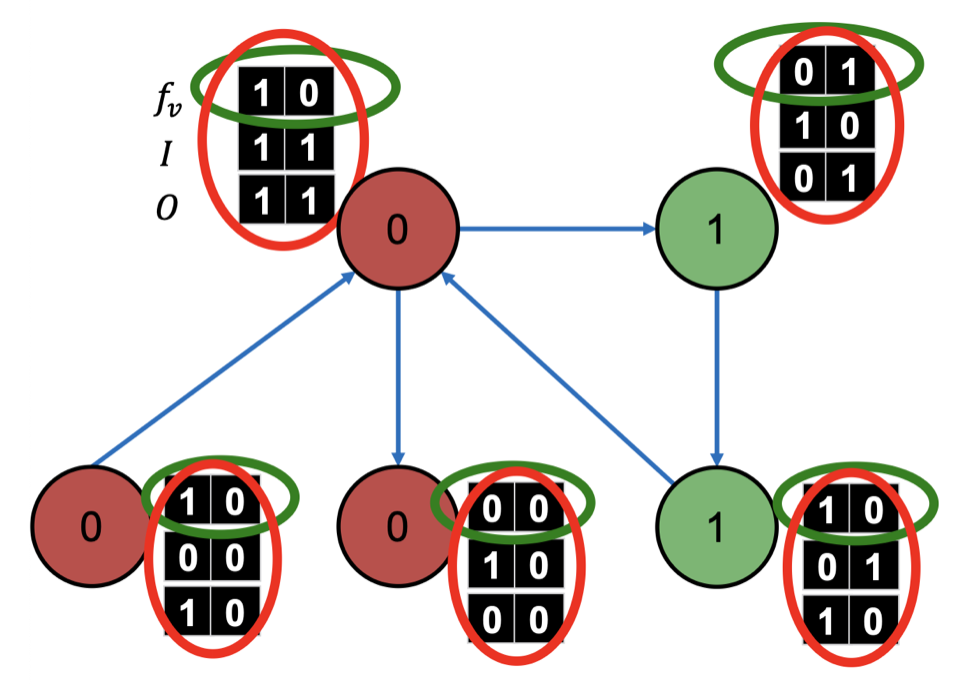
먼저 는 이웃 Node의 Class 정보를 담고 있는 Vector이며 Incoming/Outcoming Node에 대해 구분하여 담고 있다. 만약 이면, Class=0 인 이웃 Node(Incoming)가 1개임을 의미한다.
① Phase 1. Classifier 학습 (in Training Set)
먼저 Training Set를 사용해서 Classifier를 학습한다.
은 아래의 초록색 정보만 사용하고, 는 빨간색 정보를 사용해서 를 예측한다.
② Phase 2. Classifier 적용 및 반복 (in Test Set)
앞서 학습 된 Classifier를 사용해서 Test Set의 Unlabeled Node의 Class를 예측한다.
-
Classifier 를 사용하여 예측 및 업데이트
을 사용해서 주어진 Node의 속성 를 활용해 Class 를 예측하고, 이를 기반으로 이웃 Node Class에 대한 요약 정보인 를 업데이트한다.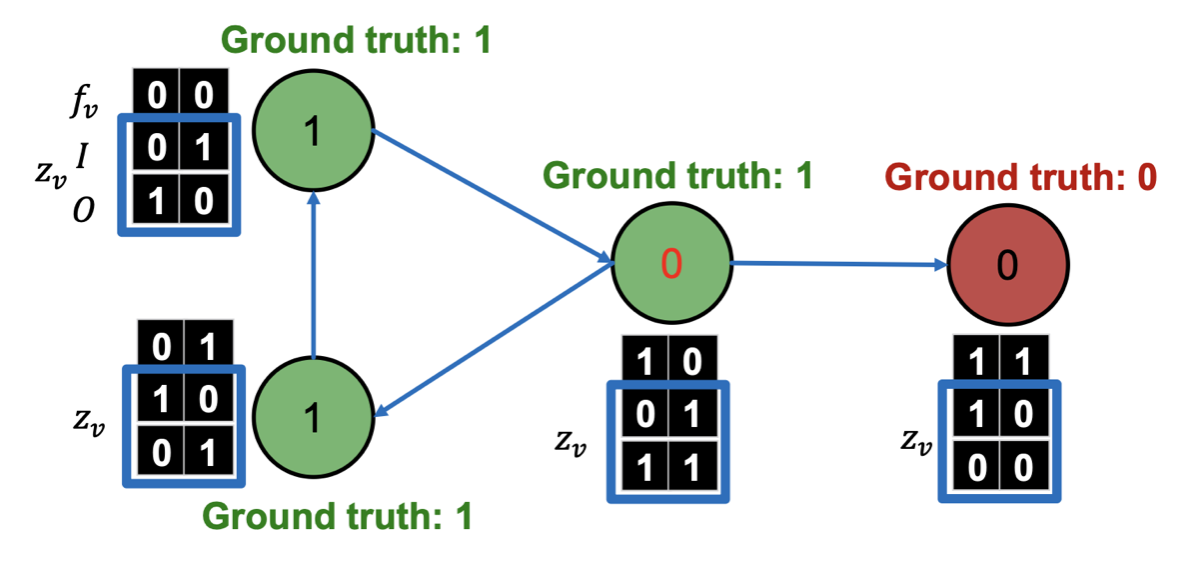
-
Classifier 를 사용하여 업데이트
새롭게 업데이트 된 와 정보를 사용해서 로 Class 를 예측하고 업데이트한다.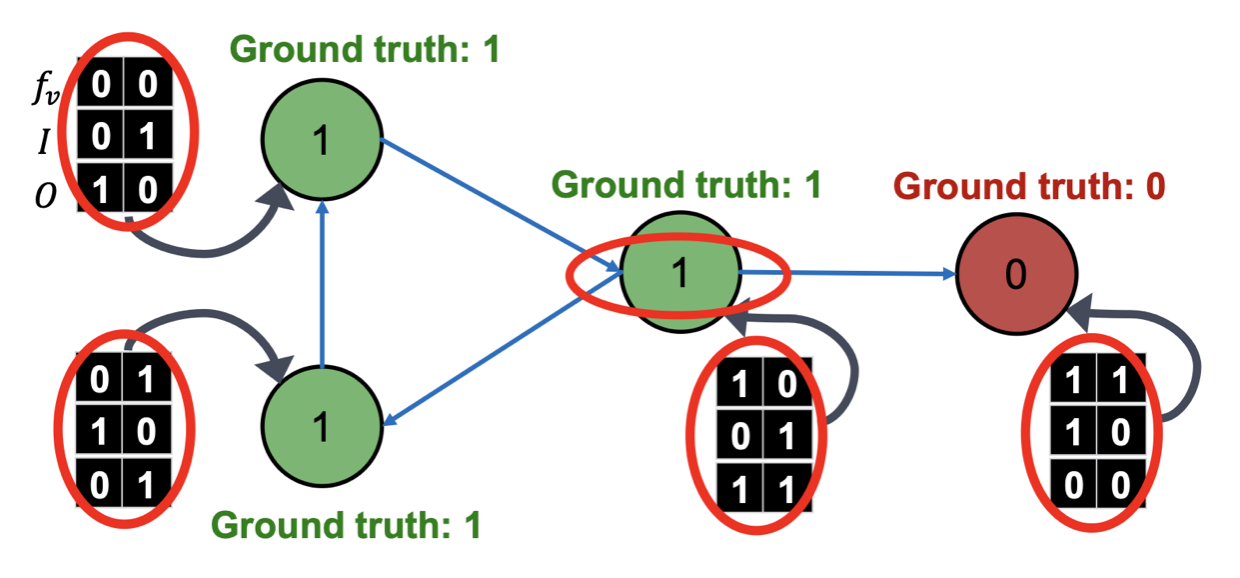
Belief Propagation
Belief Propagation은 Dynamic Programming 관점에서 접근한 방법이고, 이전 Node에서 전달받은 정보(Message)를 현재 Node의 정보와 결합해서 새로운 Belief를 계산해 업데이트 하고 다시 다음 Node로 전달하는 Message Passing 방식을 사용하며 이를 Graph 전반에 반복하여 적용시키는 것을 Loopy BP 알고리즘 이라고 한다.
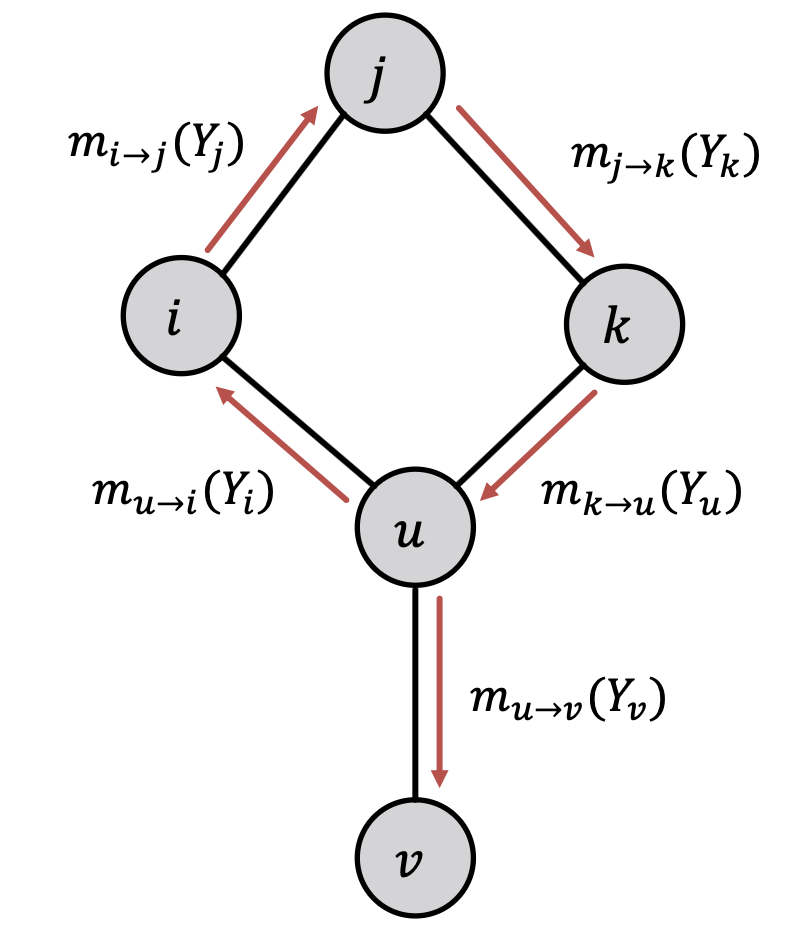
1️⃣ Message Passing
먼저 Message Passing 방식에 대해 살펴보자. Cycle이 없는 Path 및 Tree 구조에서의 Message Passing 방식은, Node의 순서를 정하고 순서에 따라 Belief를 계산 후 이를 전달하여 마지막 Node까지 진행해나간다.
각 Node에서는 Update Belief 동작이 일어나며, 이 때 이전 Node의 Message와 현재 Node의 정보를 결합해서 Belief를 계산한다. Path 구조에서는 In-Link에서 Out-Link 방향으로 진행되며 Tree 구조에서도 마찬가지로 In-Link(Leaves)에서 Out-Link(Root) 방향으로 Message Passing이 진행된다.
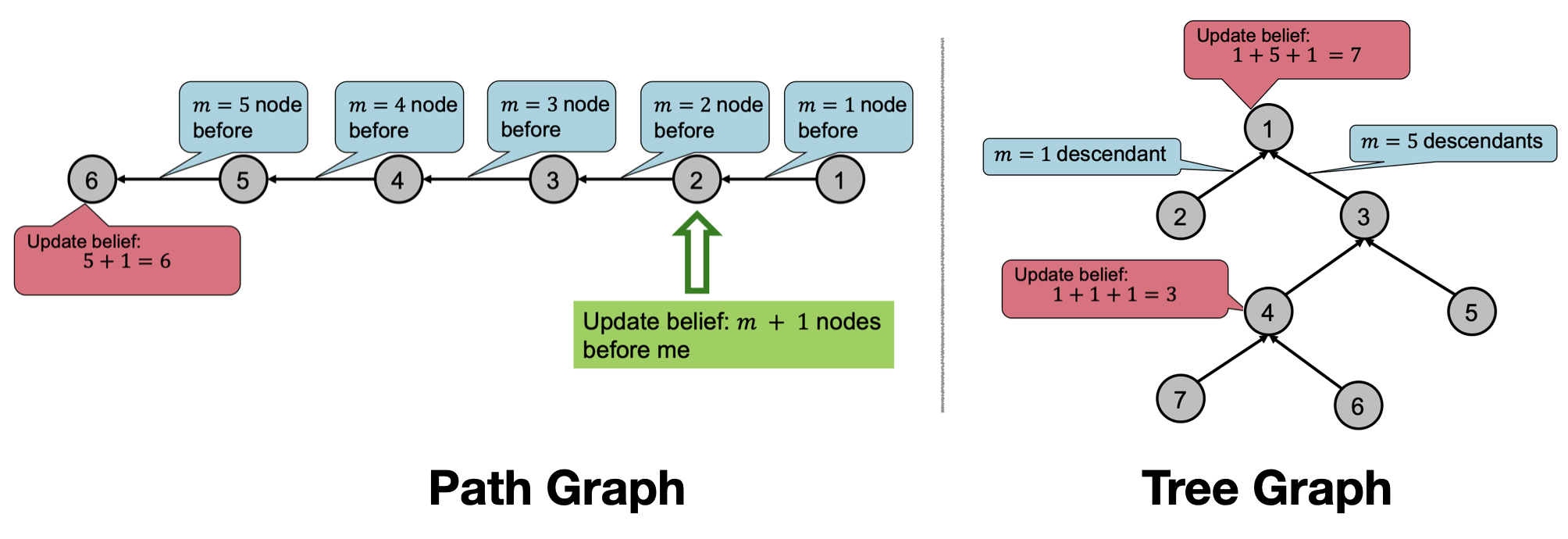
2️⃣ Loopy BP
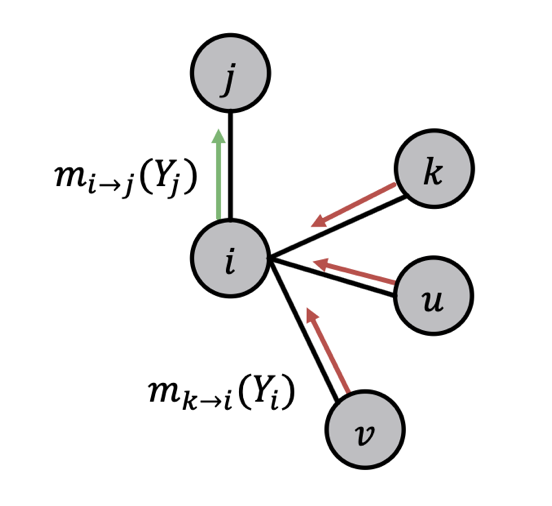
앞서 설명한 Message Passing을 Graph 구조에 적용한 것이 Loopy BP 알고리즘이며, 여기서도 동일하게 이전 Node의 Belief를 다음 Node로 전달하게 된다. 아래에서 Loopy BP 알고리즘에서 어떻게 Message와 Belief를 계산하는지 확인할 수 있다.
Notation
먼저 아래 수식에서 사용되는 Notation의 의미는 아래와 같다.
| 기호 | 의미 |
|---|---|
| Label-label potential matrix, Node 가 Class 일때 Node 가 Class 일 확률 | |
| Node 의 Prior belief, Node 가 Class 일 확률 | |
| Node 의 Message, Node 가 Class 에 속할 확률에 대한 추정치 | |
| 모든 Class(Label)의 집합 |
기존에 사용되던 이론인 Homophily는 이웃 Node 간의 Class가 유사할 확률을 의미하지만 여기서 사용되는 Label-label potential matrix는 이웃 Node 간의 Class가 다를 확률을 구하며, 기존 방식들과 달리 Homophily에 대한 의존성을 낮춘다.
수식 및 알고리즘
① Initialize: 모든 Message를 1로 초기화한다.
② Repeat: Message 업데이트 과정을 반복한다.
Node 에 대한 Message를 계산할때는, 이웃 Node의 Message를 합하는 과정에서 Node 를 제외하고 계산하며, 각각의 Class별로 해당 Message를 계산한다.
또한 앞어 Path/Tree 구조와 달리 Graph 구조에서는 Node의 순서를 결정할 수 없기 때문에 임의의 Node에서 시작한다.
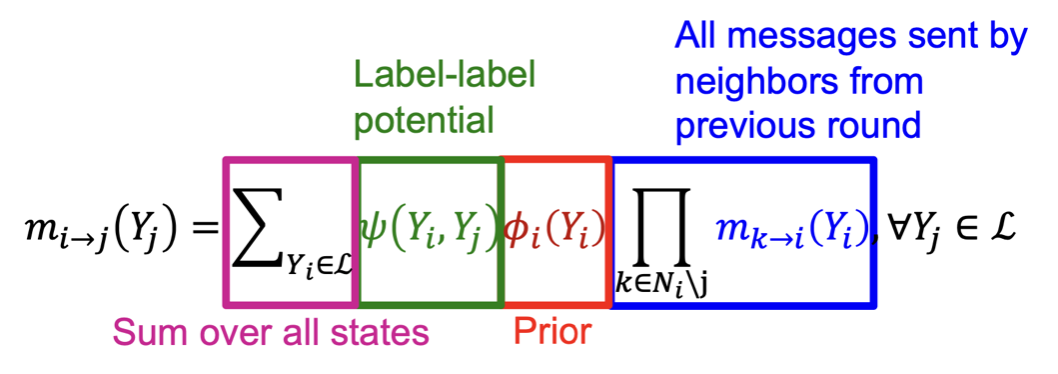
③ Belief: Message가 수렴하는 경우, 해당 Node에 대한 Belief를 계산한다.
Message가 수렴하면 해당 Node에 대해서 Class별로 Belief(해당 Class에 속할 확률)을 구해서 Class를 구분한다.
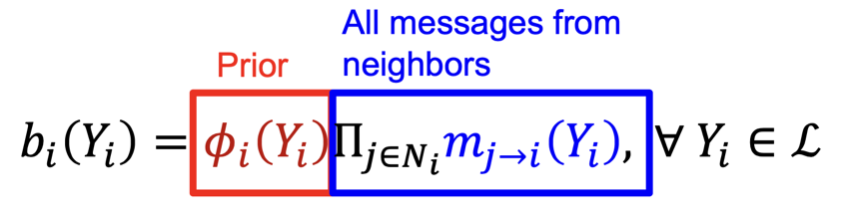
아래 그림과 같이 Graph 구조에 Cycle이 강한 경우 Message가 수렴하지 않아 알고리즘이 정상적으로 동작하지 않지만, 실제 문제에서는 Cycle이 길거나 약한 상관관계 내에서 존재하기 때문에 Loopy BP 알고리즘이 정상적으로 동작하고 많이 활용한다.