기초인공지능 #2 Informed Search

Kyeongmin·2024년 3월 23일

대학원

목록 보기

3/27

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.

개요

이전에는 목표(Goal)에 대한 정보가 없는 Uninformed Search에 대해서 알아봤다면, 이번에는 목표에 대한 정보를 가지고 더 최적화 된 탐색을 수행하는 Informed Search에 대해서 알아보려고 한다.

Heuristic

Heuristic 정의

현재 상태가 목표 상태까지 얼마나 가까운지 추정하는 함수
- Fringe(관심 대상)에 A / B 가 있을때 A가 B보다 더 좋다는 정보를 얻을 수 있음
각 탐색 문제에 별도로 설계된 함수

예시

각 도시별 목적지까지의 직선거리(오른쪽)는 휴리스틱의 한 예시이다.
여러 도시가 주어졌을때, 어떤 도시가 더 좋은 선택지인지 알 수 있다.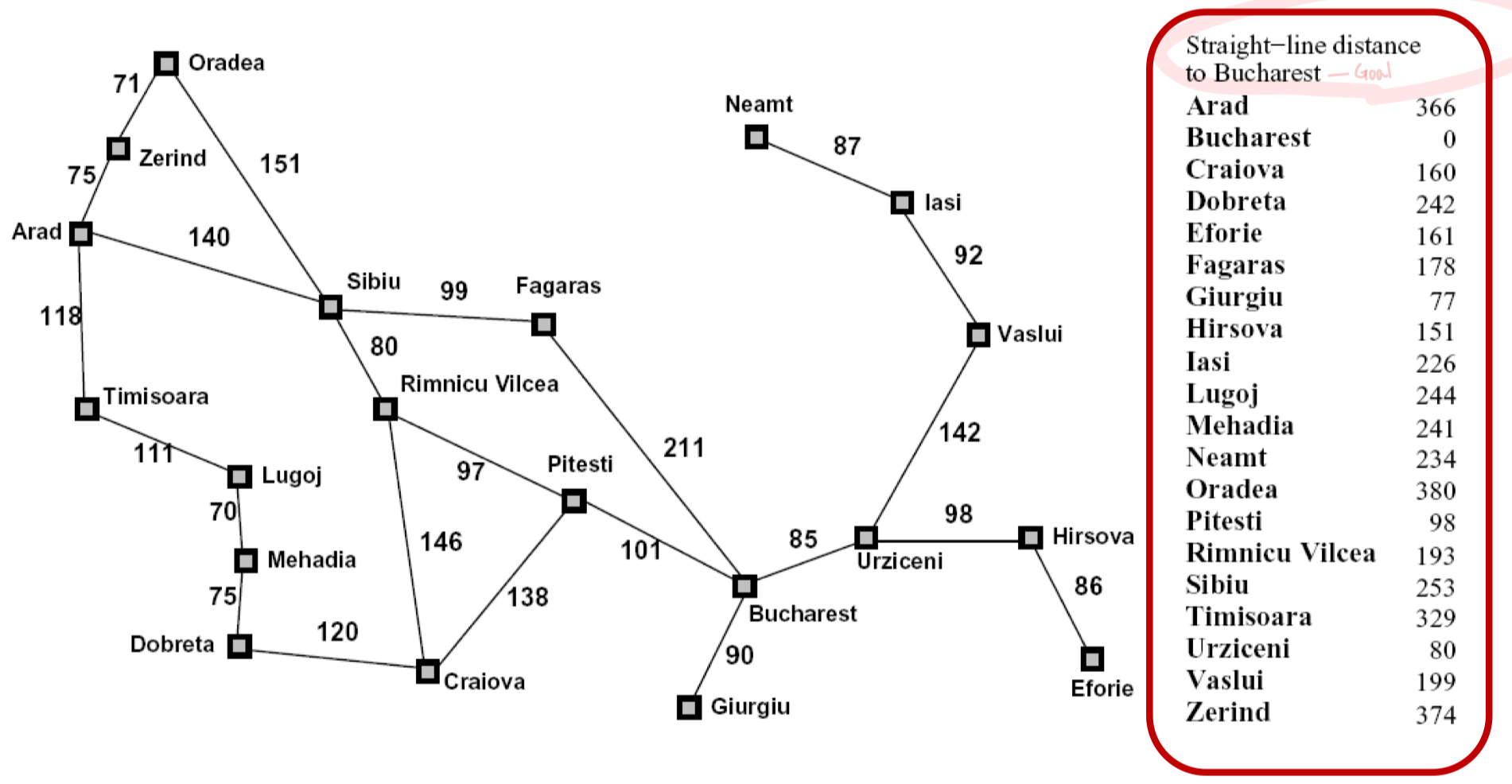

Greedy Search

$h(n)= Heuristic$ 을 통해서 목표와 가까운 정도를 추정하고, 가장 가깝다고 추정되는 Node를 선택한다.
다만 Greedy Search는 실제값이 아닌 추정값을 기반으로 다음 Node를 선택하기 때문에
간단한 문제에서는 잘 동작하지만, 최악의 경우 DFS를 사용할 경우와 비슷하다.

A* Search

1. A* Search란

$\textbf{A}^*$ Search는 $h(n)$ 의 한계를 보완하는 알고리즘이다.
$\textbf{A}^*$ Search는 n까지의 실제 비용 $g(n)$ , 목표까지의 추정 비용 $h(n)$ 을 더한 $f(n)$ 을 사용한다.

f(n) = g(n) + h(n)

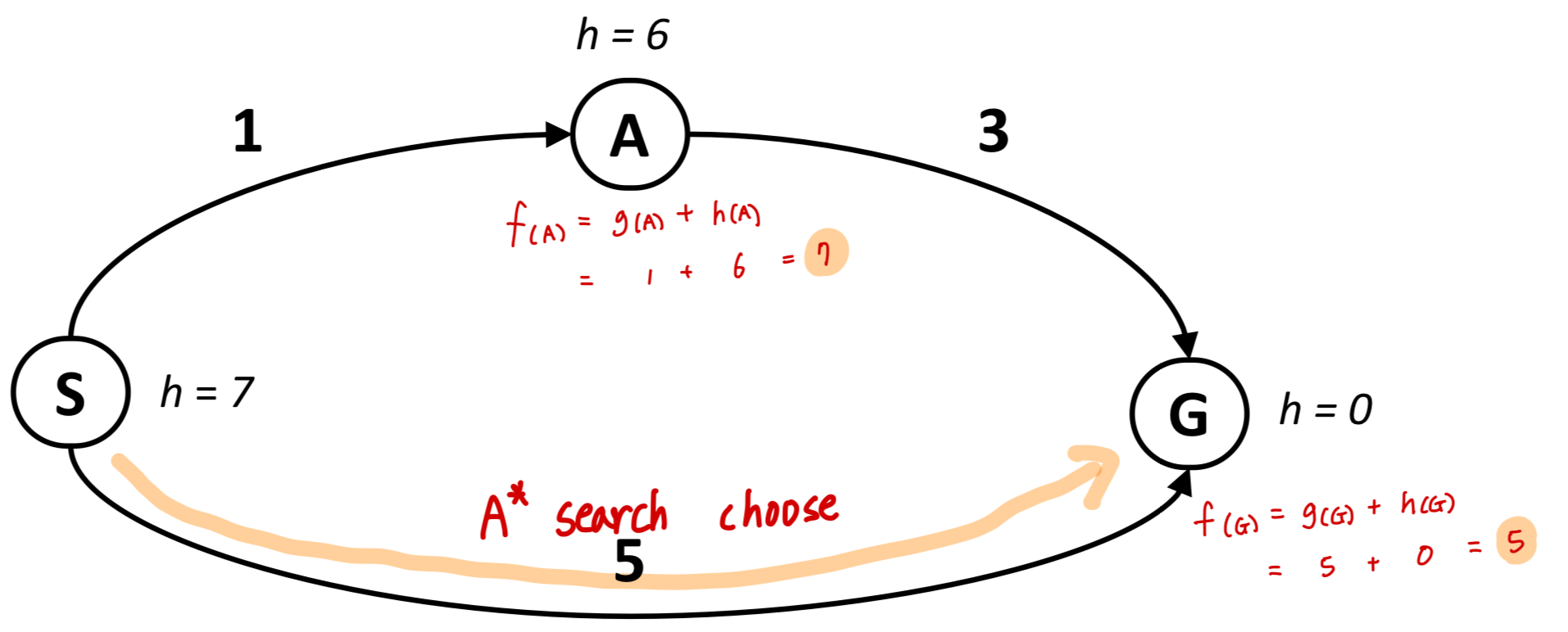
A* Search 를 사용한 예시를 들어보자.

위 그림에서 실제 최단거리는 [S, A, G] 이지만, A* Search를 사용하면 [S, G]를 선택하게 된다.
S-A로 이동할때의 f(n) 값은 7이지만, S-G로 이동할때의 f(n) 값은 5이기 때문에 최단거리인 A로 이동하지 않고 바로 G로 이동하게 된다.

위 그림을 보았을때 우리는 A* Search가 최적의 답을 찾아낸다고 말할 수 있을까?
이런 문제를 보완하기 위해 A* Search에서는 Admissible Heuristic을 사용해야 한다는 조건이 있다.

2. Admissible Heuristic이란?

Heuristic은 실제 Cost를 추정하는 값이므로 실제 Cost와 다른 값을 가질 수 있다.
Admissible Heuristic은 추정된 값이 실제 값보다 작거나 같아야 한다는 조건이 붙는다.
이를 수식으로 표현하면 아래와 같다.

0 \;\leq\; h(n) \;\leq\; h^*(n) \quad\vert\quad h^*(n)=\text{true cost to a nearest goal}

만약 위 예시에서 Admissible Heuristic을 사용한다면,
$0 \leq h(S) \leq 5,\;0 \leq h(A) \leq 3$ 이어야 한다.

Admissible Heuristic을 찾는 것에 대해선 다른 글에서 설명할 예정이다.

3. A* Search의 증명

그렇다면 Admissible Heuristic을 사용했을 때 A* Search가 정말 최적의 답을 찾는지 확인해보자.
아래 그림과 같이 최적해 A, 일반해 B(최적은 아닌 다른 해), 최적해 A의 조상 중 하나인 n이 있을때,
B, n이 Fringe에 있다고 가정해보자.

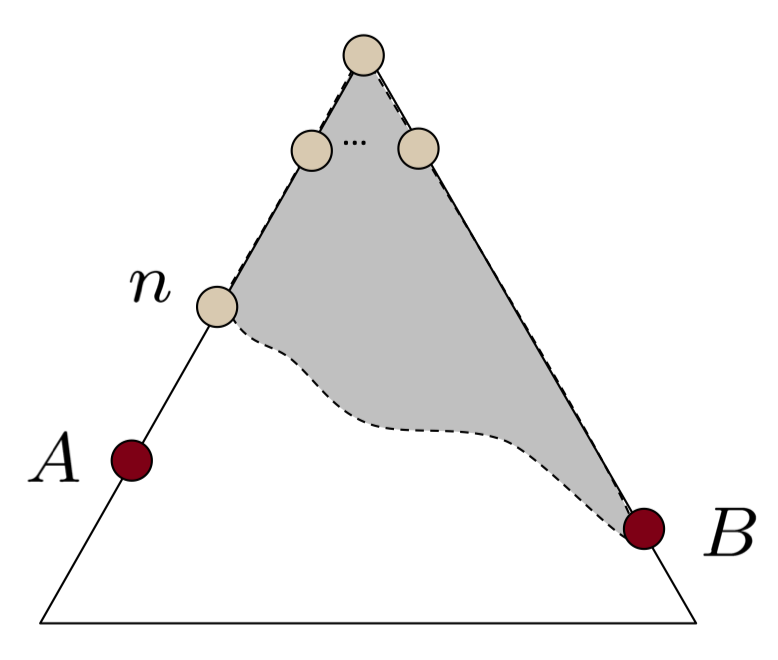
A* Search가 정말 최적해를 찾는다면, 일반해 B보다 n을 먼저 확인해야한다.
이 과정을 증명해보자.

1. f(n)은 f(A)보다 작거나 같다.
$f(n),\,f(A)$ 에 대해서 수식으로 표현하면 아래와 같다.

\begin{aligned} f(n)&=g(n)+h(n)\\ f(A)&=g(A)+h(A) \end{aligned}

우리는 Admissible Heuristic(추정값은 실제값보다 작거나 같음)을 사용하고 있기 때문에,
A→A 지점까지의 실제값은 0이고, 추정값은 이보다 작거나 같아야 하기 때문에 $h(A)=0$ 이다.

그럼 아래와 같이 축약할 수 있다.

\begin{aligned} f(n)&=g(n)+h(n)\\ f(A)&=g(A) \end{aligned}

여기에서 $g(A)=g(n)+g(n\rightarrow A)$ 와 같이 나타낼 수 있고,
$h(n)$ 은 n 지점부터 A 지점까지의 값을 추정한 값이므로 $g(n\rightarrow A)$ 의 값을 추정한 값이라고 할 수 있다.

이를 정리하면 아래와 같고, 결국 $f(n)\leq f(A)$ 를 증명할 수 있다.

\begin{aligned} f(n)&=g(n)+h(n)\\ f(A)&=g(n)+g(n\rightarrow A)\\ h(n)&\leq g(n\rightarrow A) \qquad\qquad\dots\; f(n) \leq f(A) \end{aligned}

2. f(A)은 f(B)보다 작거나 같다.
$f(A),\,f(B)$ 에 대해서 수식으로 표현하면 아래와 같다.

\begin{aligned} f(A)&=g(A)+h(A)\\ f(B)&=g(B)+h(B)\\ \end{aligned}

여기서 A는 최적해, B는 최적해가 아닌 일반해이기 때문에 $g(A)\leq g(B)$ 이고,
$h(A),\,h(B)=h(A\rightarrow A),\,h(B\rightarrow B)$ 이기 때문에, $h(A),\,h(B)=0,0$ 이다.

이를 다시 수식으로 정리하면 아래와 같고, $f(A) \leq f(B)$ 를 증명할 수 있다.

\begin{aligned} f(A)&=g(A)\\ f(B)&=g(B)\\ g(A)&\leq g(B) \qquad\qquad\dots\; f(A) \leq f(B) \end{aligned}

3. A* Search에서 n은 B보다 먼저 확인된다.
1/2번 증명을 정리하면 아래 식과 같다.

f(n) \leq f(A) \leq f(B)

A* Search에서는 f 값을 가지고 Fringe에서 확인할 대상을 선택하기 때문에,
n, B 모두 Fringe에 있어도 n Node가 먼저 선택됨을 증명할 수 있고, 이는 최적해를 찾는 탐색 알고리즘이라고 할 수 있다.

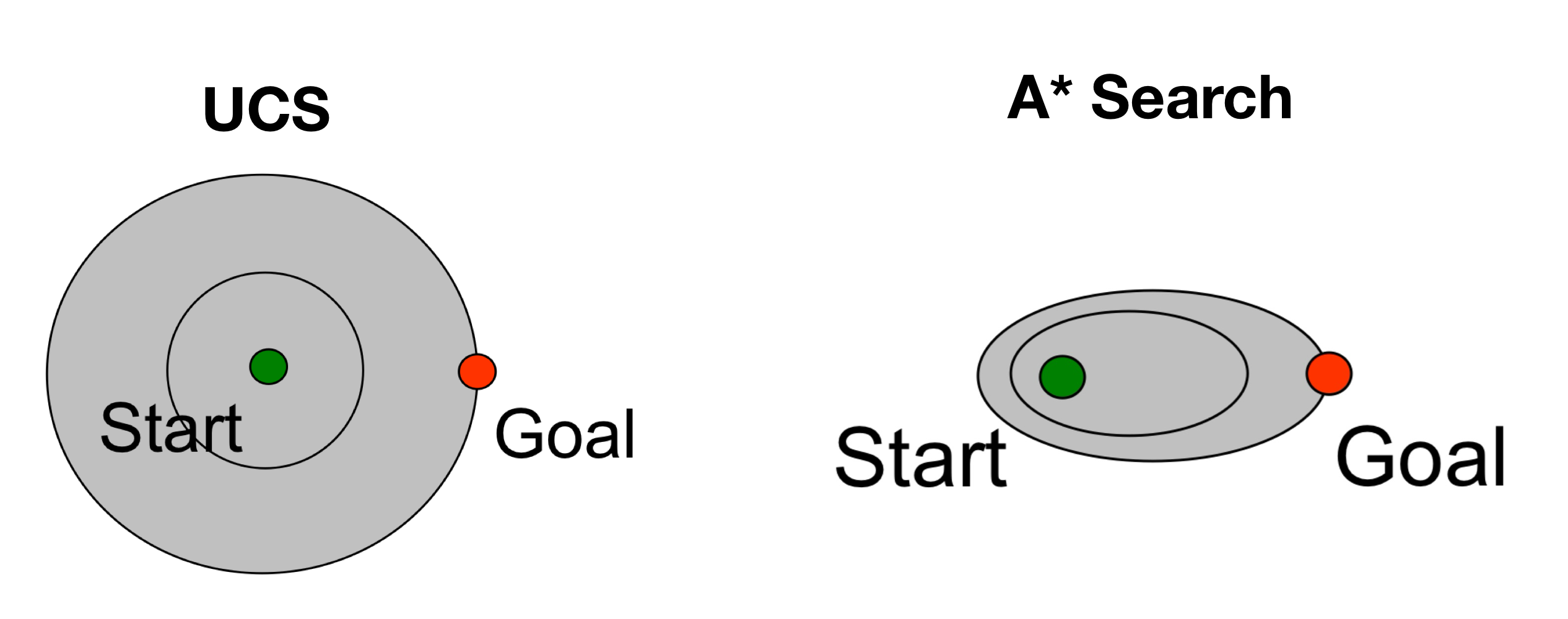
4. UCS VS A* Search

아래 그림과 같이 UCS는 모든 방향을 다 확인하지만, A* Search는 목표 지점을 향해있는 방향을 주로 확인한다.
다만 A* Search의 성능은 Heuristic의 성능에 따라 달라지게 되는데
Heuristic의 추정치가 0에 가까워진다면 UCS ≈ A* Search 이고,
Heuristic의 추정치가 0 이라면 UCS = A* Search 이다.