기계학습 #4 Model Selection

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

---

이전 글에서 Overfitting에 대한 정의와 이를 방지하는 Regularization에 대해서 정리했었다.
본 글에서는 Model의 상태(Over/Undefitting)를 알아내고 최적의 Model을 선택하는 Model Selection 기법들에 대해서 다룰 예정이다.

시작하기에 앞서, 우리가 Ridge Regression Model을 만든 후 새로운 데이터에 대해 평가해보았을 때,
굉장히 큰 Error가 발생하면 우리는 어떻게 대처할 수 있을까?

앞에서 배운 내용에 따르면 Model 성능이 낮은 이유는
Underfitting $L_{train} \uparrow, L_{test} \uparrow$ / Overfitting $L_{train} \downarrow, L_{test} \uparrow$ 2가지가 있었고,

이를 개선하기 위해 아래 방법들을 시도해 볼 수 있었다.
Underfitting 개선 : 많은 Feature(X인자) / 복잡한(다항식) Feature / 적은 Regularization($\lambda$)
Overfitting 개선 : 많은 학습 데이터 / 적은 Feature(X인자) / 더 높은 Regularization($\lambda$)

위의 방법들은 결국 최적의 Hyperparameter(ex. $\lambda, \text{M} \dots$)를 찾는 것이고,
이를 찾기 위한 과정을 Machine Learning Diagnostic이라고 부른다.

---

Model Selection

먼저 우리는 어떻게 최적의 Model 인지에 대해 알 수 있을까?
최적의 Model은 Under/Overfitting 어느 한 곳으로 치우쳐지지 않은 Model이라고 말할 수 있다.

그럼 우리는 Train Error, Test Error를 확인함으로써 Model이 Under/Overfitting이 되었는지 확인하여 최적의 Model 인지에 대해 알 수 있을 것이다.

Model의 성능을 조절하는 방법은 Hyperparameter를 조절하는 아래 2가지 방법이 있다.
1️⃣ Model Complexity(degree $M$) 2️⃣ Regularization parameter $\lambda$
여기에 대한 값을 얼마나 조절해야 하는지에 대한 문제가 바로 Model Selection Problem이다.

이제 Model Selection에 관련된 방법을 아래에서 다뤄보고자 한다.

1. Test Set

먼저 우리는 가지고 있는 데이터를 Train/Test Set으로 나눠서,
Train Set으로만 Model을 학습시키고 Test Set에 대해 평가해봄으로써 최적의 Model을 찾아낼 수 있다.

Model(Mapping Function)을 여러개 만들고, 각각 Train Set에 대해 학습한 이후 Test Set Error가 가장 낮은 모델을 선택해볼 수 있다.

다만 Test Set은 평가를 위한 데이터지, Model을 학습시키고 선택하는 과정을 위한 데이터가 아니다.
Test Set을 Model Selection에 사용하게 된다면 결국 Model 은 Test Set에 Overfitting 될 수 있다.
그리고 여기엔 잘못 된 가정이 있다. 우리가 미래의 데이터를 알 수 없듯이, 우리는 Test Set을 가질 수 없다.

이런 문제점과 가정에도 불구하고 현재의 데이터를 통해 일반화 된, 최적의 Model을 구하기 위한 시도들이 존재한다.

2. Validation Set

데이터를 Train / Validation / Test Set 3종류로 나눠보자.
동일하게 Train Set으로만 모델을 학습시키고 Validation Set에 대한 평가 결과를 통해 Model을 선택함으로써 모델이 Test Set에 Overfitting 되는 것을 피하고 온전히 평가용으로만 사용할 수 있다.

다만 여기서도 똑같은 문제가 발생한다.
Test Set은 아니지만 결국 Validation Set에 Overfitting 된다는 문제이다.
또한 여전히 Validation Set $\neq$ Test Set 이라는 문제점도 존재한다.

3. K-Fold Cross-Validation

단일 Validation Set을 이용했을때의 문제점을 극복하기 위한 방법이 K-Fold Cross Validation 이다.
여기에선 데이터를 K개의 Set로 나누고, K번 학습을 반복하며 각각의 Set를 한번씩 Validataion Set으로 가정하여 평가 결과를 확인하는 방법이다.

최적의 모델을 선택하는 방법에는 여러가지가 있지만 간단하게 소개하자면,
1️⃣ N개의 모델 중 K개의 학습에 대한 평가 결과가 좋고 표준편차가 낮은 모델 선택
2️⃣ K개의 데이터 세트 중 가장 낮은 Loss를 가진 모델 선택
이 외에도 다양한 방법이 있으니 참고만 하길 바란다.

다만 K-Fold Cross-Validation은,
$N_{model} \,\times\, K_{data}$ 번 학습을 진행해야 하기 때문에 계산 비용이 많이 들게 되고, 모든 Hyper parameter의 경우의 수를 다 확인해 볼 수 없다는 단점이 존재한다.

Bias-Variance Problem

지금까지 최적의 모델을 선택하기 위해 Test Error를 확인하는 방법들에 대해서 다뤘다.
여기에서는 Error 가 가지고 있는 속성에 대해서 얘기해보고자 한다.

우리는 Error 를 아래 2가지로 나누어 정의할 수 있다.

• Error due to Bias : 모델의 예측값과 실제값과의 차이에 의한 Error $(\approx \text{Underfitting})$
• Error due to Variance : 모델 예측값의 변동성에 의한 Error $(\approx \text{Overfitting})$

글로만 보면 잘 이해가 되지 않아서,
Bias / Variance를 그림으로 나타내면 아래처럼 4가지 경우로 나눌 수 있다.

• Bias ⬇️ / Variance ⬇️ : 가장 이상적인 경우로써 우리가 찾고자 하는 모델
• Bias ⬆️ / Variance ⬇️ : 예측값과 실제값에 비해 편향되어 있는 경우 $(\approx \text{Underfitting})$
• Bias ⬇️ / Variance ⬆️ : 예측값의 변동성으로 실제값에 비해 퍼져 있는 경우 $(\approx \text{Overfitting})$
• Bias ⬇️ / Variance ⬇️ : 가장 최악의 경우

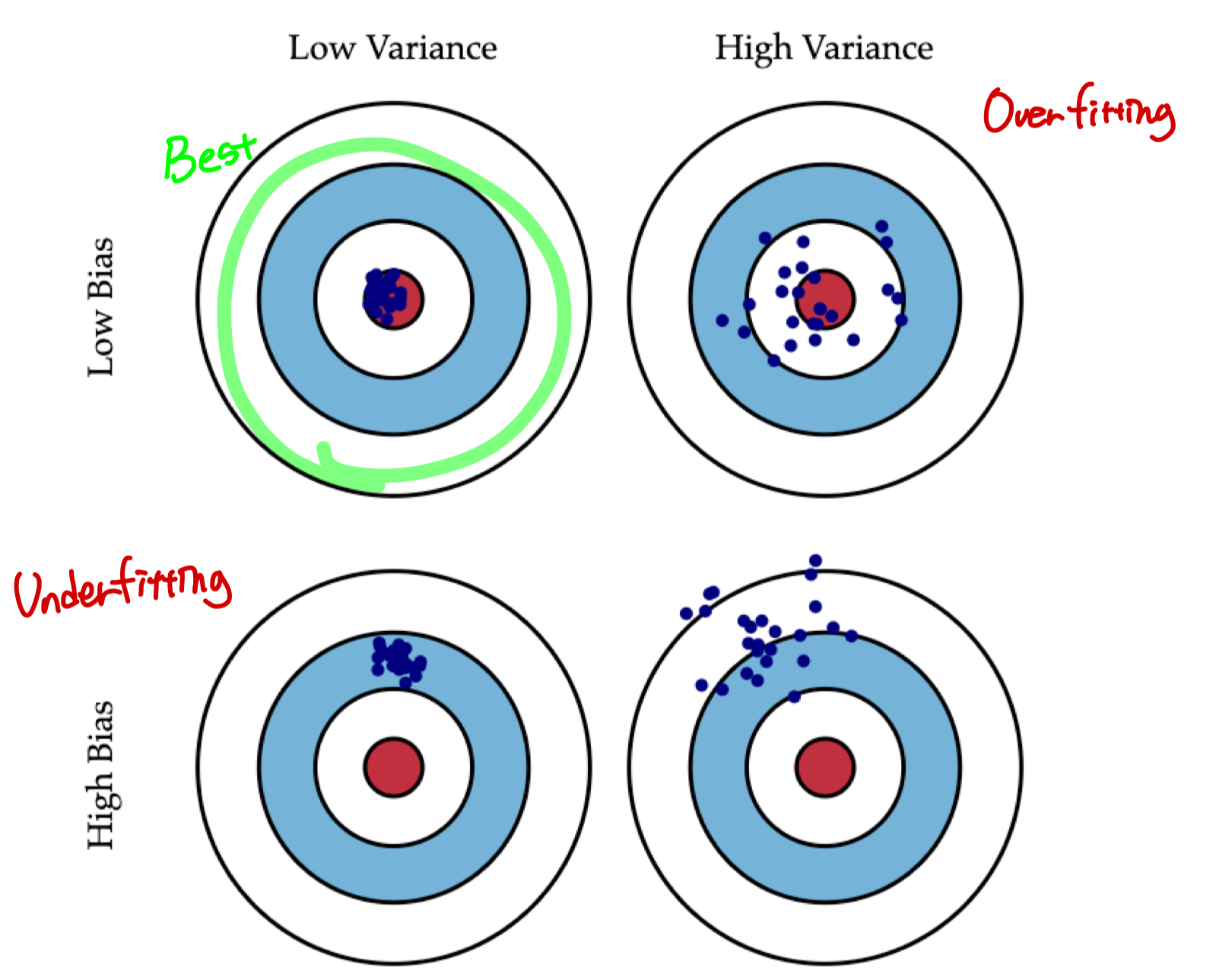
Bias-Variance Tradeoff
아래 그림처럼 Bias, Variance 모두 낮게 할 수는 없다.

(그림은 여기 사이트에서 참조하였다.)

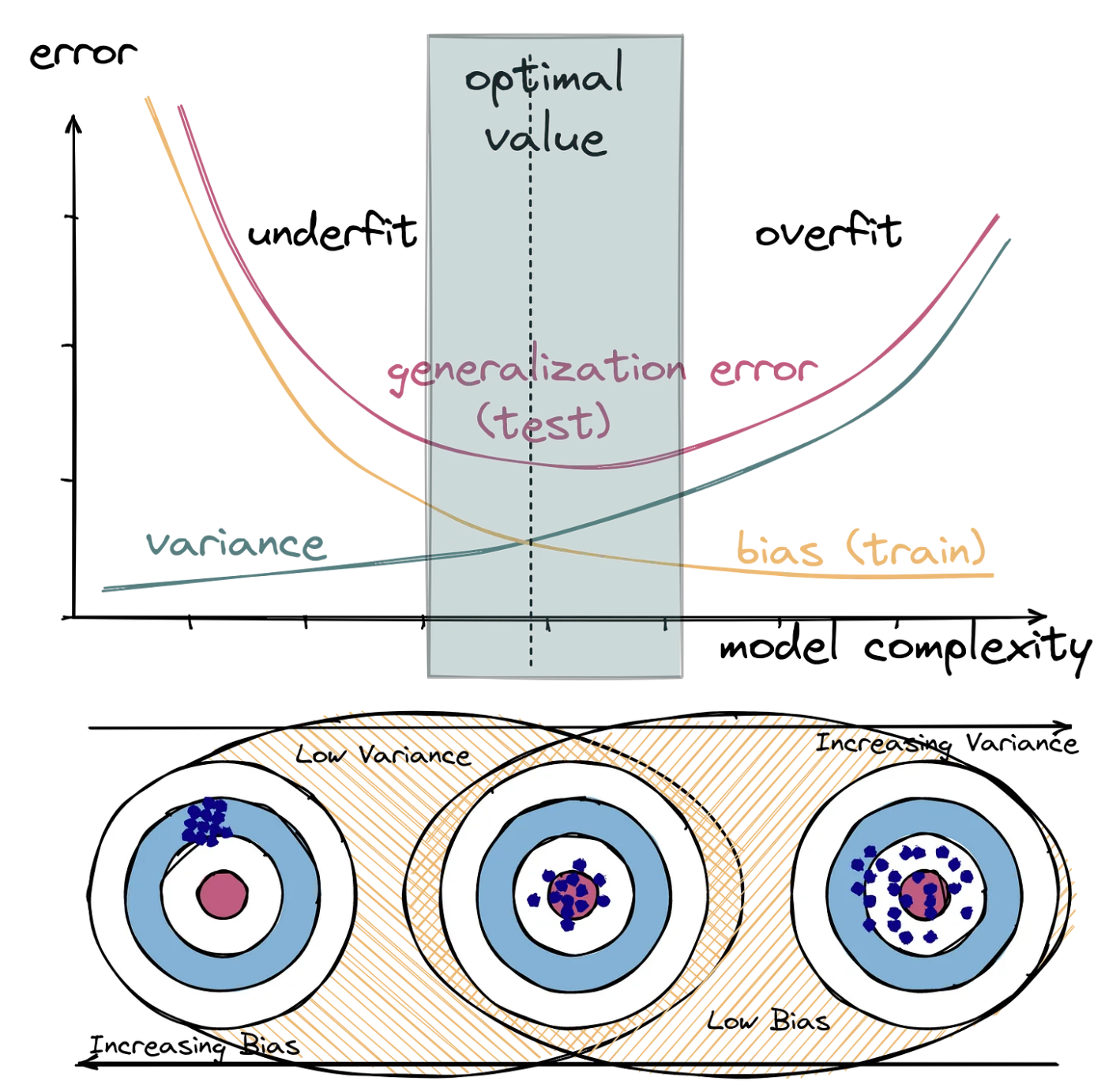
Regularization with Bias-Variance

Regularization은 복잡한 모델을 간단하게 만드는 방법으로 $\lambda$를 통해서 강도를 조절할 수 있다.
즉 $\lambda$의 크기에 따라서 Bias-Variance는 아래와 같은 관계를 지니게 된다.
$\text{Large}\,\lambda \Rightarrow \text{High Bias (Underfitting)} \;,\;\text{Small}\,\lambda \Rightarrow \text{High Variance (Overfitting)}$

Training set size with Bias-Variance

Training set size 또한 Bias-Variance와 밀접한 관계를 지닌다.
Training set size의 증가는 High Varinace(=Complex Model)에 도움이 될 수 있지만,
High Bias(=Simple Model)에는 도움이 되지 않는다.