기초인공지능 #6 Adversarial Search

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.

---

Adversarial Search(적대적 탐색)을 의미 그대로 생각해보자.
어떤 상대방과 경쟁하는 것 같고, 겨뤄야 할 것 같은 느낌이 든다.
체스, 바둑과 같은 예시를 들어볼 수 있고, 이렇게 상대방과 경쟁하는 게임에 사용되는 방법이
바로 Adversarial Search이다.

Game

게임에는 아래와 같이 여러 유형이 있다.

• Deterministic(결정론적) / Stochastic(확률론적)
• Perfect(완전) / Partial(부분) Information
• N-Players
• Zero Sum

게임의 종류에 따라 우리가 모든 상태(경우의 수)를 알 수 없는 경우가 있는데,
이는 우리가 모든 상태에 대해 시뮬레이션 함으로써 어떤 경로가 최적해임을 알 수 없다는 것을 의미한다.
즉 최적해에 대한 Sequece of action을 구할 수 없다는 것이다.

이런 경우에 우리가 게임 문제에 대한 탐색을 통해 찾고자 하는 해는,
주어진 상태에 따라 최선의 행동을 추천해줄 수 있는 strategy(policy)이다.

1. Formalizations

먼저 Deterministic game에 대해서 공식화함으로써 간단하게 나타내보고자 한다.
Deterministic game을 공식화하는 방법에는 여러 방법이 있고, 아래는 그 중 하나이다.

• States : $S$
• Players : $P=\{1, \,\dots\, , N\}$
• Actions : $A$
• Transition Function : $S\times A \rightarrow S$
  Planning Search에서의 Successor의 기능이라고 생각하면 된다.
  주사위 같이 확률적인 Action을 사용한다면 복잡도가 높아진다.
• Terminal Test : $S \rightarrow \{t,f\}$
  Planning Search에서의 Goal Test와 유사한 개념이지만,
  Game에서는 특정한 Goal, 즉 해를 찾는 것이 아니기 때문에 Game의 종료 여부를 확인한다.
• Terminal Utilities : $S\times P \rightarrow R$
  Game이 종료되었을 때의 결과, 즉 Reward를 의미하며 이를 통해 게임의 승자를 확인할 수 있다.
  해당 값을 높이는 방향으로 탐색하여 게임을 승리할 수 있게 해야한다.
• Solution : $S \rightarrow A$
  이전에 언급했던바와 같이 찾고자 하는 해는 Policy이다.
  즉 주어진 상태에서 어떤 행동을 할 것인지 추천해주는 Policy를 찾는 것이다.

2. Zero-Sum Game

Adversarial Search는 여러 유형에서 사용되지만, 본문에서는 Zero-Sum 게임을 주로 다룰 것이다.
Zero-Sum Game은 여러 Agent가 서로 상반된 목적(Utilities)을 가지고 경쟁하는 게임을 말한다.
예로써 어떤 Utility에 대해 A는 maxmize, B는 minimize 하는 경우를 말할 수 있다.

Adversarial Search

Adversarial Search를 통해 풀고자 하는 문제는 나 뿐만 아니라 상대방이 존재하는 경우에 대한 문제이고,
그렇기 때문에 탐색 과정에 상대방이 어떻게 행동할지에 대해서 가정하고 예측하는 것이 포함된다.

1. Single-Agent Tree

먼저 기존의 Planning 문제를 위에서 다뤘던 공식을 통해 나타내보자.

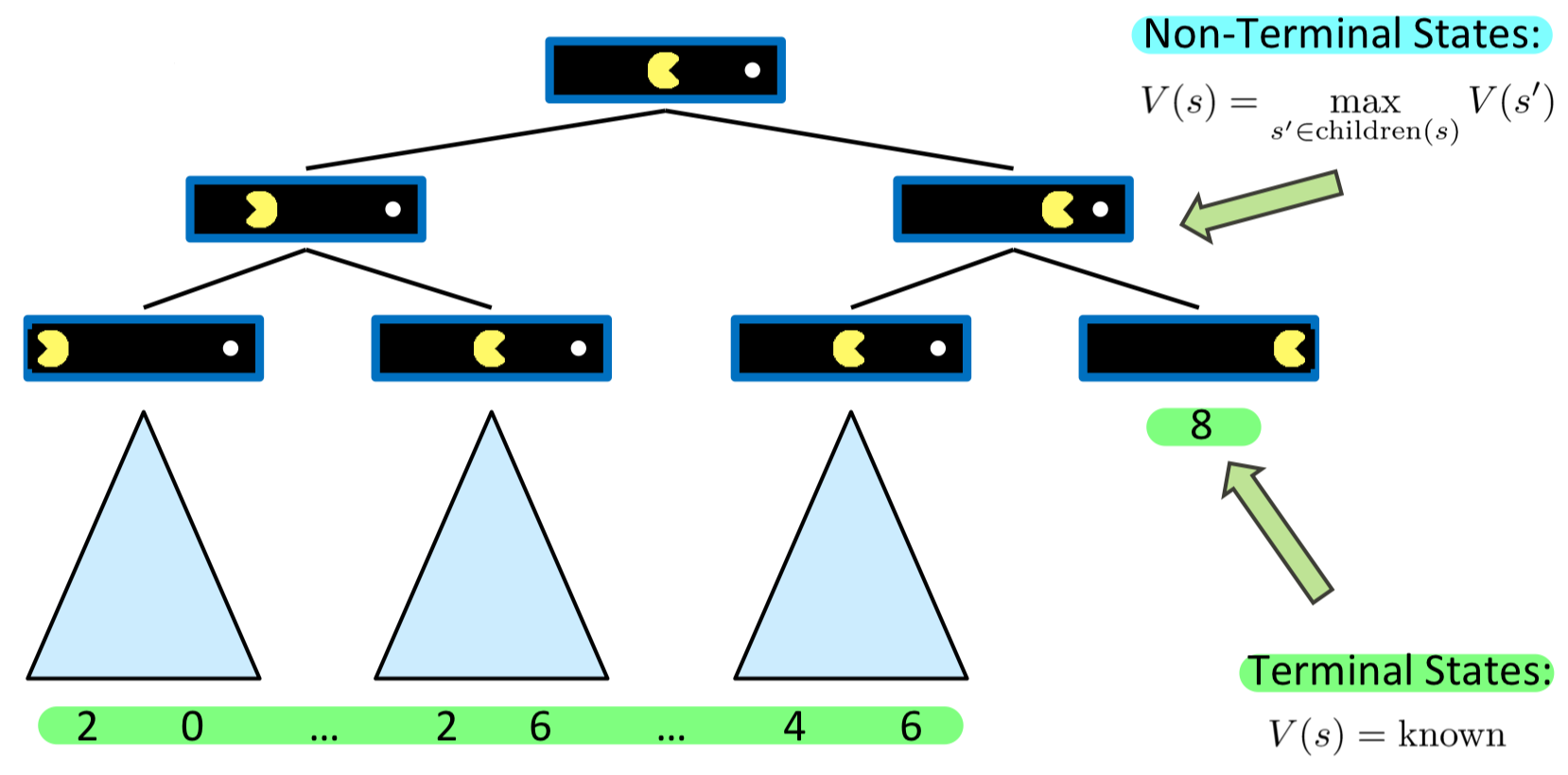
위의 그림에서 각각의 파란 상자는 States $S$이고, Action $A$을 통한 다음 State를 나타낸 Tree 구조이다.
$\text{Terminal Test} = \{t\}$인 마지막 States는 Terminal States 이고,
그렇지 않은 States는 Non-Terminal States 이다.

Terminal States 에서의 값(Utility)는 정해져있기 때문에 $V(s) =\text{known}$
Non-Terminal States 에서는 높은 값을 가지는 방향으로 행동해야 하고,
이는 높은 값을 가지는 자식 노드쪽으로 행동하는 것을 의미하기에
$V(s)=\underset{s'\in\text{children}(s)}{\operatorname{max}}V(s')$

2. Adversarial Game Tree

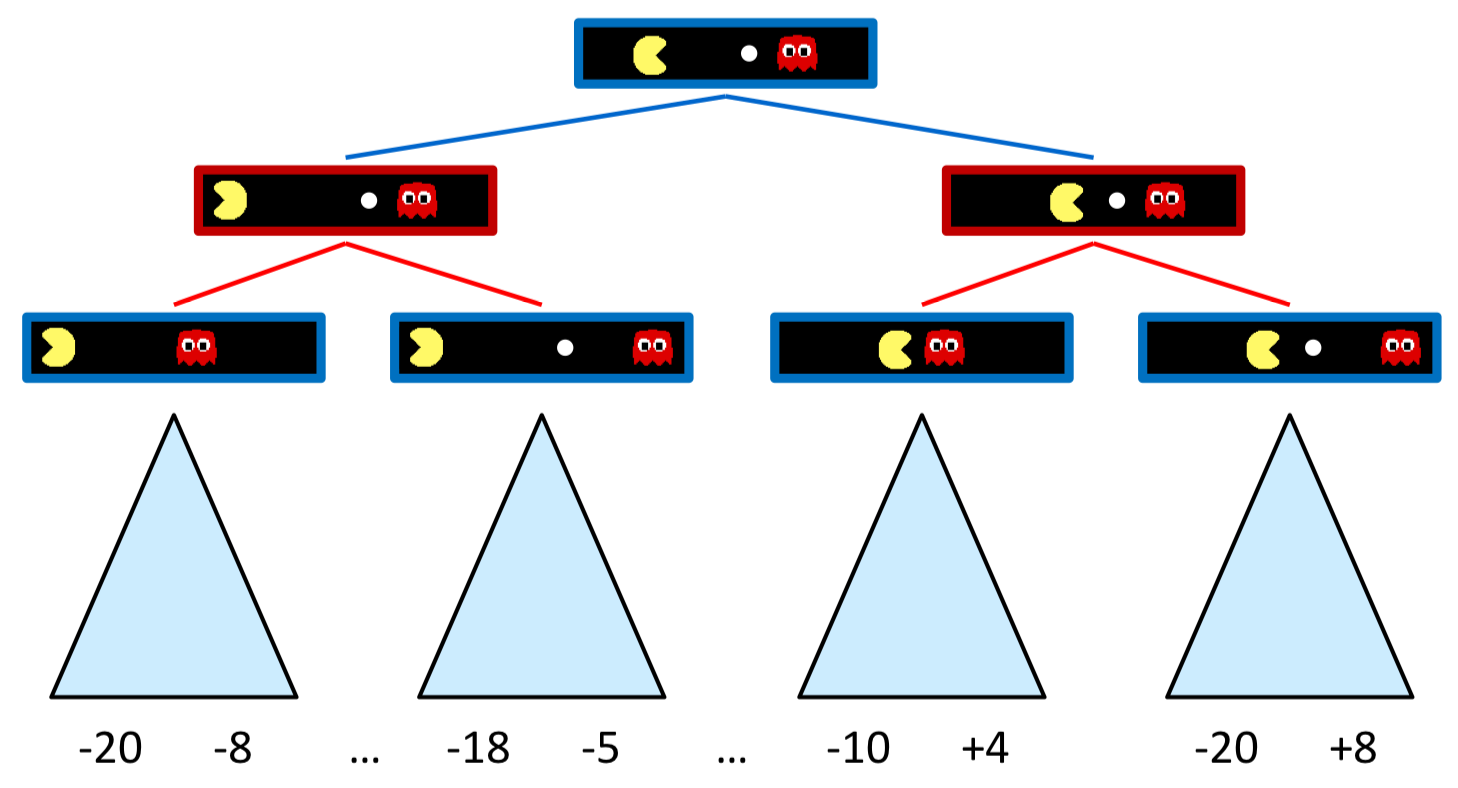
그렇다면 본래 풀고자 했었던 게임을 Tree 구조로 나타내보자. 먼저 나를 포함한 여러 Agent가 존재하고, 나 → 상대방 순으로 이동하여 게임이 종료될 때까지 반복하는 문제라고 생각해보자.
모든 경우의 수를 그려보아도, 상대방이 어떻게 행동할 것인지 모르기 때문에 이전처럼 무작정 좋은 점수를 향해서만 탐색할 수 는 없다. 문제에서 최고점은 8점(가장 오른쪽)이고, 이를 향해서 이동한다고 해도 상대방의 행동에 따라서 최고점 8점이 아닌 최저점 -20점을 얻게 될 수도 있기 때문이다.

---

그럼 우리는 어떻게 접근해야지 Adversarial Search 문제를 잘 풀어낼 수 있을까?
먼저 상대방이 어떻게 행동할지에 대한 가정에 따라 MiniMax Search(상대방은 항상 최선의 행동을 수행), Expectimax Search(상대방은 확률에 따라 행동을 수행)으로 나눌 수 있다.

MiniMax Search

1. 정의

간단하게 생각해보면 나는 점수를 최대화하는 것이 목표지만, 상대방은 내 점수를 최소화하는 것이 목표라고 가정해 볼 수 있다. 그렇다면 우리는 이러한 가정 아래 Adversarial Game Tree에서 상대방의 행동을 예측해볼 수 있을 것이다.

그렇다면 위에서 Terminal / Non-Terminal States 에서 얻을 수 있는 값에 대해 수식화한 것과 같이
여기에서 Terminal / Non-Terminal(Agent , Opponent) 로 나누어 수식화할 수 있다.

• Terminal States : $V(s) =\text{known}$
• States Under Agent`s Control : $V(s)=\underset{s'\in\text{children}(s)}{\operatorname{max}}V(s')$
• States Under Opponent`s Control : $V(s')=\underset{s\in\text{children}(s')}{\operatorname{min}}V(s)$

아래 그림과 같이 Terminal States가 존재한다면,
상대방은 각각의 States 중에 최저점을, 나는 각각의 States 중에 최고점을 얻을 수 있는 상태를 고를 것이기 때문에 최종적으로 -8점을 얻을 수 있다.

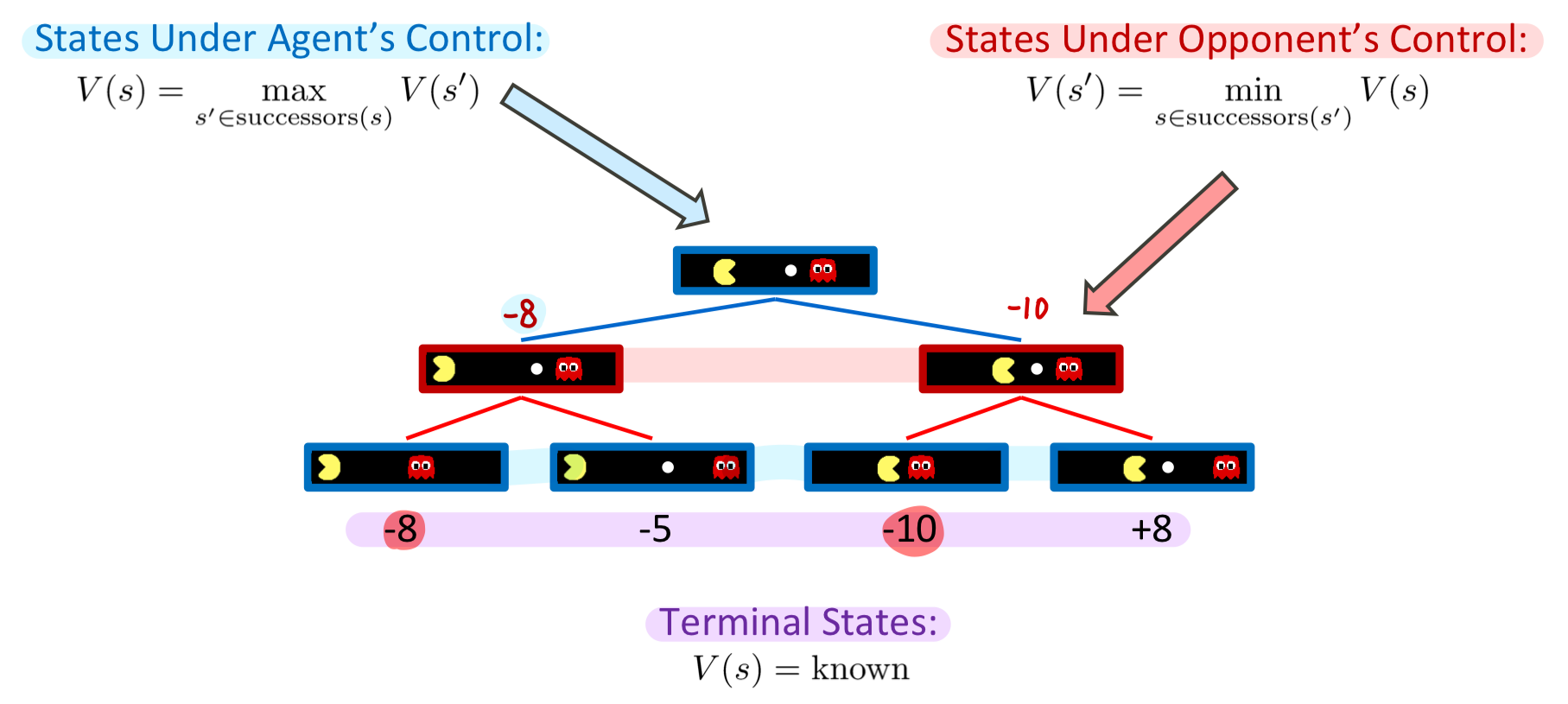
이렇게 나는 점수를 최대화 / 상대방은 최소화하는 방법을 Minimax 라고 한다.
이러한 방법은 Deterministic / Zero-Sum 게임에 활용되며, 예로는 Chess / Tic-tac-toe 등이 있다.

기존의 Planning과 유사하게 State Space Search Tree를 탐색하는 방법이며,
Minimax의 Strategy는 각각의 Agent가 최적의 행동을 수행한다는 것이다.

특징

Minimax의 효율성을 생각해보자.
먼저 Minimax는 Terminal States를 알기 위해서 마지막 Node까지 탐색해야 하고, 해(최고점)을 알기 위해서는 모든 Node를 탐색해야만 한다. 따라서 exhaustive DFS 와 유사하게 동작한다고 말할 수 있다.
또한 Minimax는 상대방이 항상 최저점, 즉 Optimal Action을 취한다는 가정이 있기 때문에,
Minimax가 Optimal을 보장하는 경우는 아래와 같다.
$\text{Opponent}=\text{optimal}\Rightarrow\text{Minimax}=\text{optimal} \\ \text{Opponent}\neq\text{optimal}\Rightarrow\text{Minimax}\neq\text{optimal}$

• Time Complexity : $O(b^m)$
• Space Complexity : $O(bm)$

또한 우리가 가지고 있는 자원은 한정적이고, 어떤 게임에서는 시간 제한이 존재하기 때문에
모든 Node를 탐색해야 하는 Minimax로 문제를 풀기에는 한계가 존재한다.
Chess의 경우에는 $b\approx35, m\approx100$ 이기 때문에 사실상 Minimax로는 풀기 어렵다.

Pseudo Code

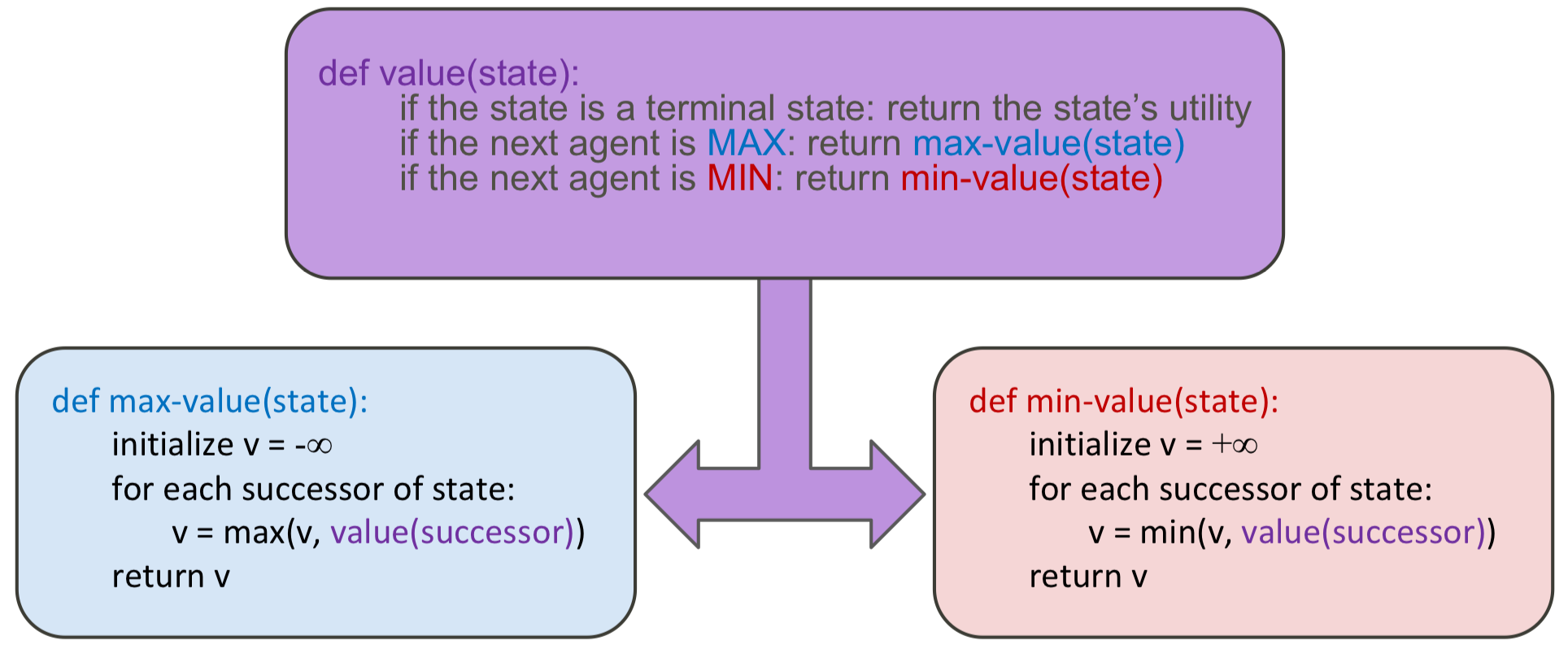
2. Alpha-Beta Pruning

이런 문제를 보완하고자 나온 방법이 Pruning 기법을 적용한 Alpha-Beta Pruning이다.

과연 우리는 모든 Node를 다 탐색해야만 할까? 결론부터 말하면 그렇지 않다.
만약 같은 상위 Node를 가진 하위 Node라면, 이미 탐색했던 다른 하위 Node의 값에 따라 다른 하위 Node의 탐색 여부를 결정 지을 수 있다.

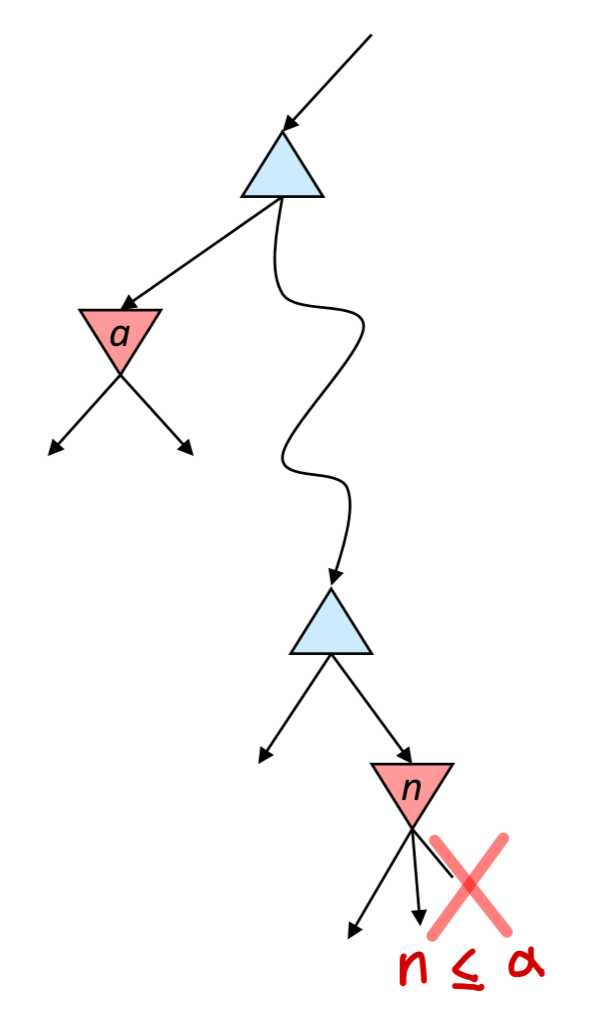
아래의 예시에서는, 만약 어떤 Min Node에 $\alpha$가 존재하고 다른 하위의 Min Node에 $n$이 존재할 때,
$\alpha \ge n$이라면 $n$의 형제 Node들은 탐색하지 않아도 된다.

왜나면 상위의 Max Node는 결국 $\alpha$를 선택할 것이기 때문이다.

(Alpha-Beta Pruning 시뮬레이션 아래 링크 참고 부탁 바란다.)

여기

특징

해당 방법에서 사용되는 용어를 조금 설명하자면 아래와 같다.

• $\alpha$ : 상위 Node에서의 Max Node가 가지고 있는 최댓값
• $\beta$ : 상위 Node에서의 Min Node가 가지고 있는 최솟값
• $\alpha-cut$ : Min Node에서 해당 Node의 값 $v \leftrightarrow \alpha$값 비교를 통한 하위 Node 삭제
• $\beta-cut$ : Max Node에서 해당 Node의 값 $v \leftrightarrow \beta$값 비교를 통해 하위 Node 삭제

Pruning의 과정은 최종적으로 우리가 찾고자하는 Root 값에는 영향이 없지만 중간 Node들이 가지고 있는 값에는 영향을 줄 수 있기 때문에 이 부분을 조심해야 한다.

만약 정렬이 잘 되어있는 Tree 구조라면, 시간 복잡도는 $O(b^{m/2})$ 이다.
다만 대부분의 문제에서는 여전히 지수 함수 형태의 시간복잡도를 가진다.

Pseudo Code

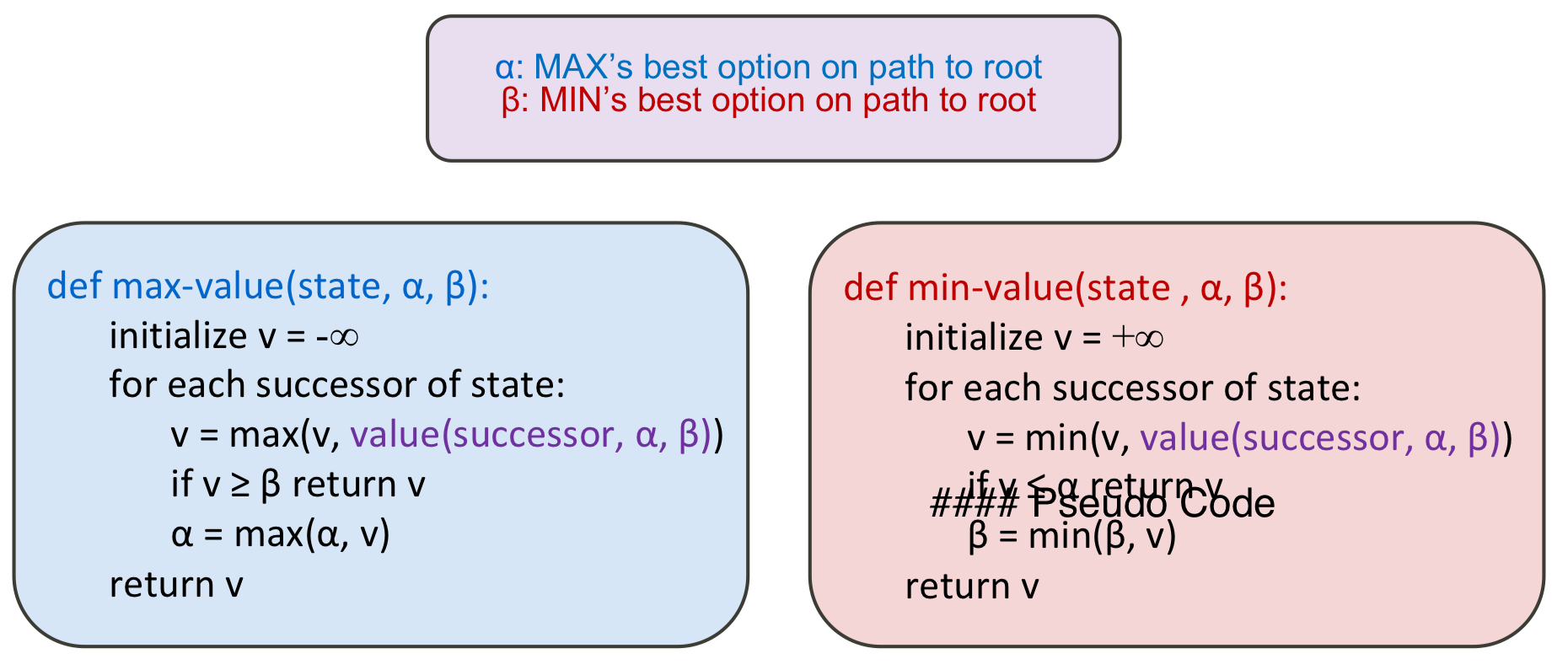
3. Depth-limited Search

정의

이전 방법들이 가지고 있는 시간 복잡도 문제를 개선하기 위한 방법이 바로 Depth-limited Search 이다.
최대로 탐색 가능한 Depth를 제한해두고, Terminal utilitiy 값을 추정함으로써 복잡도를 줄이는 방법이다.

Depth의 제한이 들어가기 때문에 이전에 다뤘던 "Iterative Deepening" 방식을 사용할 수도 있다.

다만 이 방법은 값을 추정하기 때문에 복잡도는 낮지만 Optimal은 보장하지 못한다는 단점이 있다.

Evaluation Functions

일반적으로 Evaluation Function은 특정 Feature에 대한 Weighted linear sum을 통해 구한다.

문제점

1. Complexity
   Evaluation Function은 언제나 불확실성을 가지지만, Tree 탐색의 Depth를 늘릴수록 불확실성은 줄어들기 때문에 Evaluation Function의 성능은 중요하지 않아진다.
   다만 Depth를 늘리거나, Evaluation Function(Features)의 성능을 올리는 방법 모두 복잡도가 높아지기 때문에 이를 잘 조율하는 것이 중요하다.

2. Inifinite Replanning
   Depth-limited Search에서 제한된 Depth에 따라서, Depth 제한에 의해 현재 State부터 Target State 까지 Depth에 도달하지 못해 무한 반복하는 경우가 발생할 수 있다.
   이런 Risk를 사전에 판단하여 적절한 Depth를 부여해주는 것이 좋다.

※ 참고

Alpha-Beta Pruninig은 정렬 상태에 대한 의존성이 크다.
이런 부분을 활용하여 Evaluation function을 사용하여 어떠한 Node(State)를 먼저 확인할 것인지에 대한 가이드를 제공하는 방법도 탐색 효율을 증가시킬 수 있다.

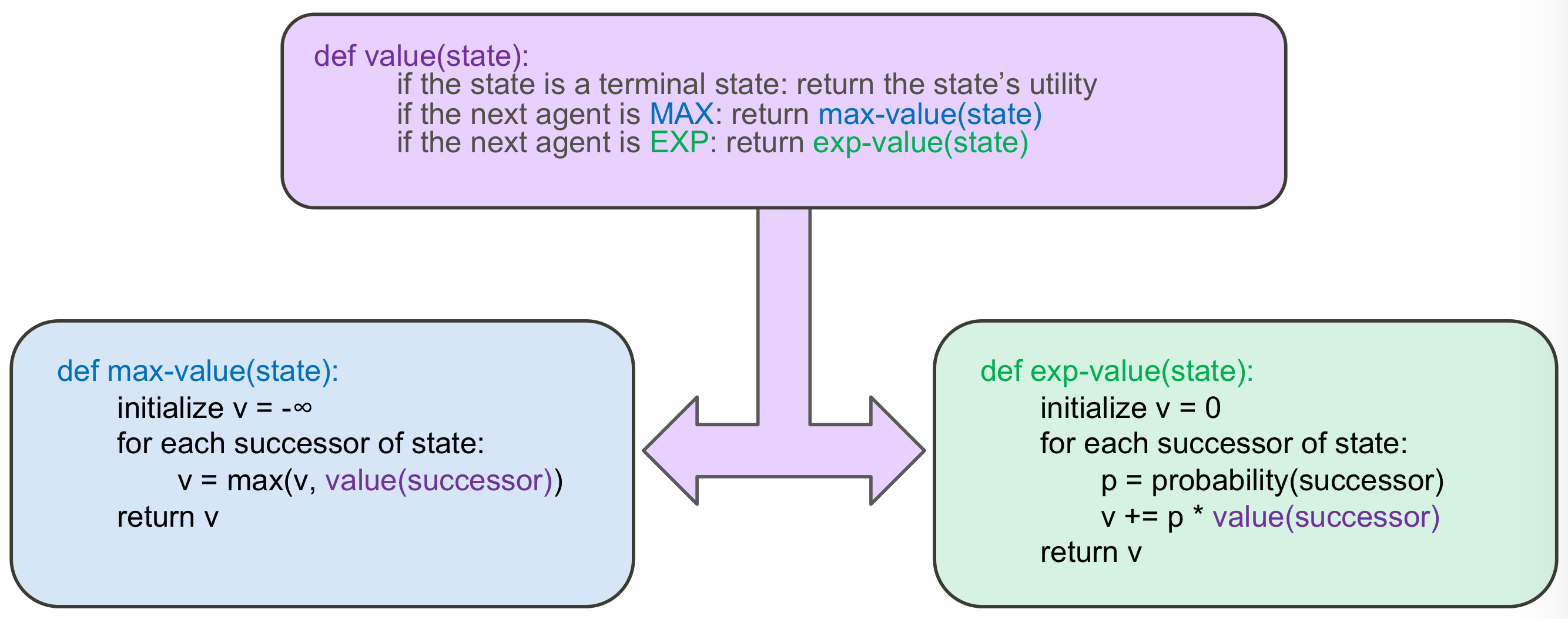
Expectimax Search

1. 정의

Expectimax Search는 Minimax Search와 다르게 상대방이 최선을 다할지, 또는 다른 행동을 수행할지가 확률에 의해서 결정된다는 차이점이 있다.

따라서 이전에 min값을 취함으로써 상대방의 행동을 예측한 것과는 달리,
여기에서는 확률을 통한 기댓값을 취함으로써 상대방의 행동을 예측해볼 수 있다.
다만 이러한 방법은 Optimal을 보장하지 못한다는 단점이 있다.

Expectimax Search에서는 아래 그림과 같이 Opponent Agent를 동그라미로 표현한다.
또한 좌측 Node의 기댓값은 아래 식과 같이 구할 수 있다.
$\text{Terminal States}(v_1,v_2,v_3) \times \text{Probability}(p_1, p_2, p_3) = \mathrm{sum}(v_1p_1, v_2p_2,v_3p_3)$

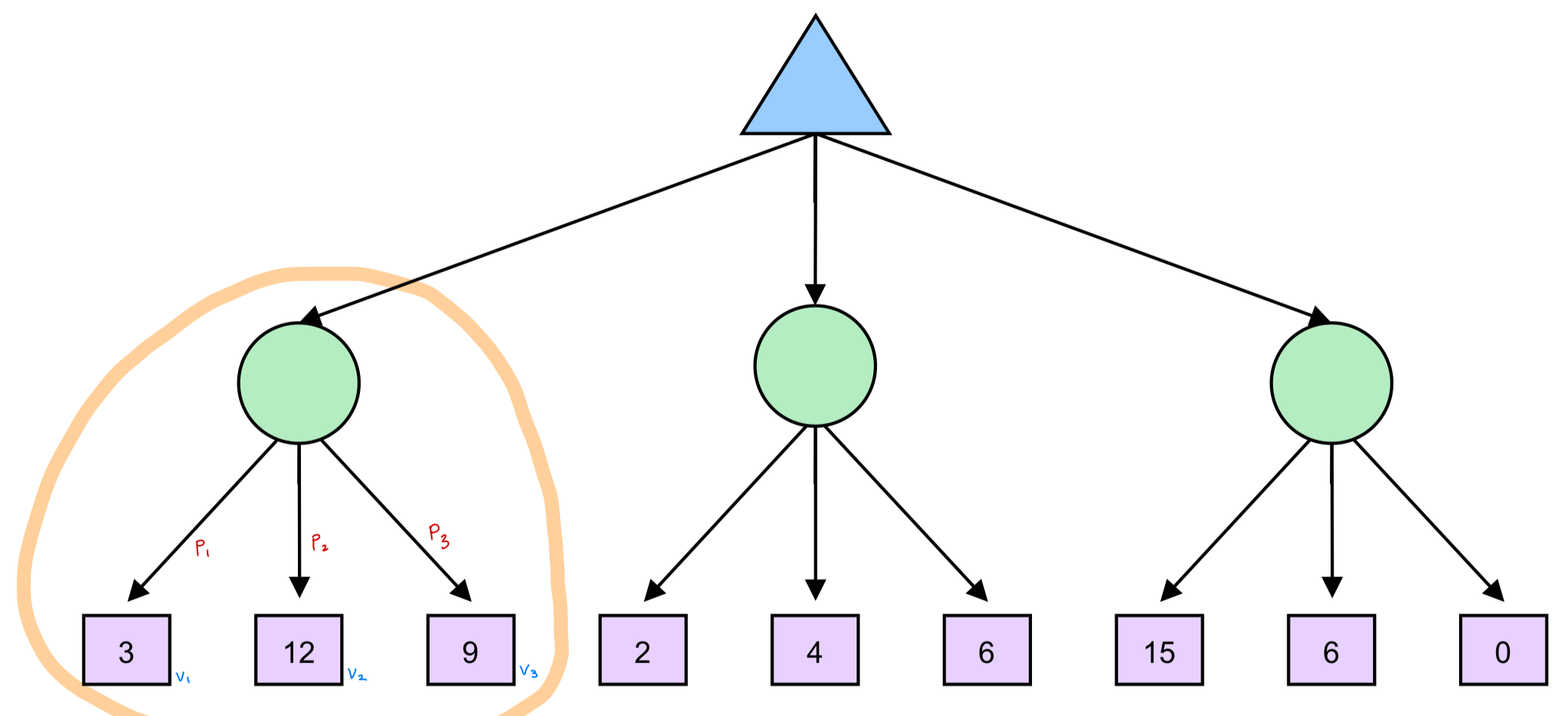
사실각 State에 대한 확률을 구하는 것은 어려운 문제이지만,
여기에서는 어떠한 방식으로든 확률이 주어졌다고 가정한 상태에서 해결하는 방식이라고 볼 수 있다.

특징

위에서 Adversarial Search의 성능 개선을 위해 ① Alpha-Beta Pruning ② Depth-limited Search 2가지 방법을 제시했었다. 하지만 여기에서 Alpha-Beta Pruning 기법은 Expectimax Search에 적용할 수 없고, Depth-limited Search 기법만 적용할 수 있다.

Minimax Search에서 하위 State 값 중 1개 값만을 상위 State 값으로 사용하지만,
Expectimax Search에서는 하위 State 값 모두가 상위 State 값으로 반영되기 때문에
Expectimax Search에서는 Alpha-Beta Pruning을 할 수 없다.

Pseudo Code