기초인공지능 #5 Constraint Satisfaction Problems

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.

---

지금까지 살펴봤던 Search Problems에 대해서 한번 생각해보자.
우리는 아래와 같은 가정을 가진 Search Problems에 대해서 살펴보고 있다.

• Single agent(단일 에이전트)
• Deterministic actions (결정된 행동, 행동에 대한 결과가 동일)
• Fully observed state (완전히 관찰된 상태)
• Discrete state space (이산형 상태 공간)

위와 같은 가정을 가진 Search Problems은, 아래 2가지로 나눌 수 있다.

• Planning(경로)
  • Solution : Path to the goal (Sequence of actions)
• Identification(식별)
  • Solution : Goal itself (Assignments to variables)

본문에서 다룰 Constraint Satisfaction Problems(이하 CSP)는
Search problems의 Identification 중 특수한 경우를 말한다.

CSP

1. CSP 정의

Search problems은 State / Goal test 를 정의할 수 있으며,
CSP 또한 Search problems이기 때문에 이를 정의할 수 있다.

• State : variables $X_i$ from domain $D$
• Goal test : set of constraints

2. 예시

1️⃣ Map Coloring

위의 문제는 인접한 지역에는 서로 다른 색깔로 칠해야 하는 문제이다.
이를 Variables, Domain 등으로 정의하면 아래와 같다.

• Variables : WA, NT, Q, NSW, V, SA, T
• Domains : $\{\text{red, green, blue}\}$
• Constraints
  • Implicit (암시적) : $\text{WA}\neq\text{NT}$
  • Explicit (명시적) : $\text{(WA, NT)}\in\{\text{(red, green), (red, blue), ...)}\}$

2️⃣ N-Queens (Formulation 1)

N-Queens는 Goal 까지의 Path가 아닌 Solution 그 자체가 중요한 문제이다.
이 문제도 아래와 같이 CSP 형태로 정의할 수 있다.

• Variables : $X_{ij}$ (보드의 전체 좌표)
• Domains : $\{0,1\}$
• Constraints
  $\forall i,j,k \;(X_{ij},\,X_{ik}) \in \{(0,0), \, (0,1), \, (1,0)\}\\ \forall i,j,k \;(X_{ij},\,X_{kj}) \in \{(0,0), \, (0,1), \, (1,0)\}\\ \forall i,j,k \;(X_{ij},\,X_{i+k,j+k}) \in \{(0,0), \, (0,1), \, (1,0)\}\\ \forall i,j,k \;(X_{ij},\,X_{i+k,j-k}) \in \{(0,0), \, (0,1), \, (1,0)\}\\$
  위의 제약조건은 꽤 복잡해보이지만, 풀어서 설명하자면
  같은 행/열 또는 대각선에는 1개의 Queen만 존재해야한다는 것을 표현한 것이다.

3️⃣ N-Queens (Formulation 2)
위와 같이 복잡한 제약 조건을 우리가 알고 있는 사전 지식을 통해서 조금 더 단순화 시킬 수 있다.
N-Queens 문제에서는 1개 열에 1개의 Queen만 배치할 수 있다.

Formulation 1에서는 변수를 보드의 전체 좌표로 설정하였는데,
사전 지식(1개 열 = 1개 Queen)을 통해 변수를 각 열마다의 Queen 좌표로 설정할 수 있다.
이렇게 변수를 만들게 되면 제약조건도 더 단순화할 수 있다.

• Variables : $Q_{k}$ (각 열의 Queen 좌표)
• Domains : $\{1,2,3,\,\dots\,, N\}$
• Constraints
  • Implicit (암시적) : $\forall i,j \; \text{non-threatening}(Q_i, \,Q_j)$
  • Explicit (명시적) : $(Q_i\,Q_j)\in\{(1,3), \,(1,4),\,\dots\}$

3. Constraint Graphs

CSP에서는 이름과 같이 Constraint(제약조건)에 대한 정의가 중요하다.
CSP의 Solution은 제약조건을 만족하는 완전한 해이기 때문이다.

이러한 Constraint을 Graph 형태로 나타낼 수 있다.
먼저 최대 2개 변수 사이에 대해서만 Constraint가 있는 경우를 Binary CSP라고 하며,
이를 Graph 형태로 나타낸 것을 Binary constraint graph이라고 한다.
Graph에서 Node = Variables, Arcs = contstraints를 나타낸다.

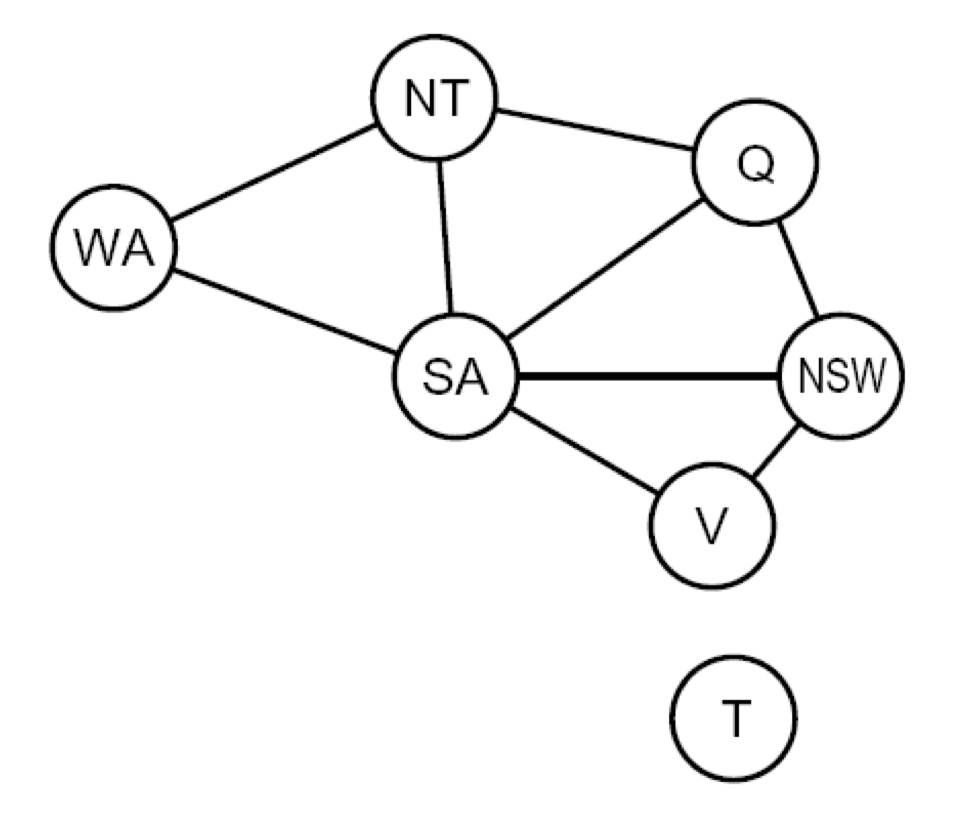
아래 그림은 Map Coloring 문제에 대해 Constraint graph로 나타낸 것이고,
해당 문제에서는 서로 인접한 2개 지역(=Variables)에 대해서만 Constraint가 존재하기 때문에
아래와 같이 표현할 수 있다.

4. CSP 유형

CSP를 정의할 때 필요한 Variables / Domain 의 특성에 따라 아래와 같이 나눌 수 있다.

• Discrete(이산형) variables
  • Finite(유한) domains
    • Domain = Boolean (Boolean CSPs)
    • $\text{Size}\;d\rightarrow \text{complete assignments }O(d^n)$ ※ n은 변수의 개수
  • Infinite(무한) domains
    • Domain = integers,strings ... (Scheduling)
• Continuous(연속형) variables
  • Domain = times

5. Constraint 유형

또한 CSP를 정의할 때 필요했던 Constraint와 Variables의 관계에 따라 아래와 같이 분류할 수 있다.

• Unary(단항) constraints : 제약조건이 1개 변수에 대해서만 관련되어 있는 경우 $(\text{SA}\neq \text{green})$
• Binary(이항) constraints : 제약조건이 2개 변수에 대해서 관련되어 있는 경우 $(\text{SA}\neq \text{WA})$
• Higher-order(고차항) constraints : 제약조건이 3개 변수 이상에 대해서 관련되어 있는 경우

그리고 우리가 앞서 다뤄왔던 Constraints는 특정 경우를 완전히 배제한다.
이러한 Constraints를 우리는 Hard Constraints 라고 말할 수 있으며,
이와 다르게 특정 경우에 대한 선호도를 나타내는 Constraints를 Soft Constraints로 말할 수 있다.

CSP 해결

위에서는 CSP에 대해서 정의 내리고, 어떠한 유형이 있는지 살펴보았다.
그럼 어떤 알고리즘을 통해서 CSP에 대한 해를 찾을 수 있는지 알아보자.

1. 기존 Search를 통한 해결

맨 처음에 정리했었던과 같이 CSP는 Search Problems 중 하나이다.
그렇다면 CSP 문제에 대해 기존 Planning 문제에 사용했었던 Search Algorithms을 적용해보자.

기존의 Search Algorithms을 적용하기 위해 CSP를 아래와 같이 정의할 수 있다.

• Initial state : Empty assignements ... {}
• Successor function : Assign value to an unassigned variable
• Goal test : ① Complete, ② Satisfies all constraints

여기에 Uninformed Search Methods 중 BFS / DFS를 적용해보면 해를 찾을 수 있지만 많은 문제가 있다.
1️⃣ BFS in CSP
CSP의 해는 Complete 하다는 특징을 가지고 있다.
해를 찾기 위해선 모든 변수에 값을 할당해야하는데, 이는 Deepest Node까지 탐색을 진행해야함을 의미한다.
결국 BFS에서는 모든 경우의 수를 메모리에 저장하고 있어야 한다는 문제점이 발생한다.

2️⃣ DFS in CSP
CSP의 해는 모든 제약조건을 만족해야하는데,
Complete 해이지만 초기의 할당값들이 제약조건을 만족하지 못할 수 있다.
기존 DFS에서는 Complete 해를 만들기 전까지 이전에 할당한 값들이 제약조건을 만족하는지 미리 알 수 없으므로 불필요한 탐색이 매우 많이 발생한다는 문제점이 발생한다.

2. Backtracking Search

CSP에서 위와 같은 문제를 해결하기 위한 Algorithm이 바로 Backtracking이다.
Backtracking은 아래의 아이디어들을 통해 위에서의 문제들을 개선하였다.

1️⃣ One Variable at a time
변수에 값을 할당할 때, 할당 순서를 고려하지 않고 할당된 값만을 고려한다.
예를 들어 $\text{[WA = red then NT = green], [NT = green then WA = red]}$ 2개 경우는 같다.
이는 변수에 값을 할당하는 순서를 고정시킴으로써 해결할 수 있다.

2️⃣ Check constraints as you go
변수에 값을 할당하기 전, 제약조건이 충돌된 경우가 없는지 확인한다.
이를 통해서 제약조건을 만족하지 못하는 경우에 대한 탐색, 즉 불필요한 탐색을 줄일 수 있다.
이러한 방법을 Incremental goal test 라고도 말한다.

DFS에 위의 2개 개선점을 적용한 Algorithm을 Backtracking Search 라고 한다.

Backtracking 성능 개선

위에서 설명한 Backtracking Search도 물론 기존 대비 성능이 우수하지만,
어떻게 효율적으로 변수의 할당 순서를 고정할 것인지 / 제약조건이 충돌되는 경우를 얼마나 빨리 확인 할 수 있는지 등에 대해서 고민해본다면, 더 성능이 좋은 Backtracking Search를 구현할 수 있을 것이다.

Backtracking Search의 성능 개선을 위한 방법은 크게 3가지로 구분할 수 있다.
1️⃣ Filtering : 해를 구할 수 없는지(제약조건을 만족하지 못하는 경우를 포함) 감지하기 위한 방법
2️⃣ Ordering : Variable(변수) 선택 / Value(값) 할당에 대한 효율적인 방법
3️⃣ Structure : 문제가 가진 구조를 통한 효율적인 탐색 방법

1. Filtering

Forward Checking

Filtering을 위한 방법으로, Forward Checking 이란 관점이 있다.

Forward Checking은 다음 방법을 통해 해를 구할 수 없는지 확인할 수 있다.

  1) 할당되지 않은 변수에 대해 할당 가능한 값의 집합을 구성한다.
  2) 변수에 값을 할당한다.
  3) 아직 할당되지 않은 변수 중 할당된 변수에 영향을 받는 변수들에 대해 값의 집합을 업데이트 한다.
  4) 아직 할당되지 않은 변수가 가지고 있는 값의 집합이 비어있다면, 해를 구할 수 없는 경우이다.

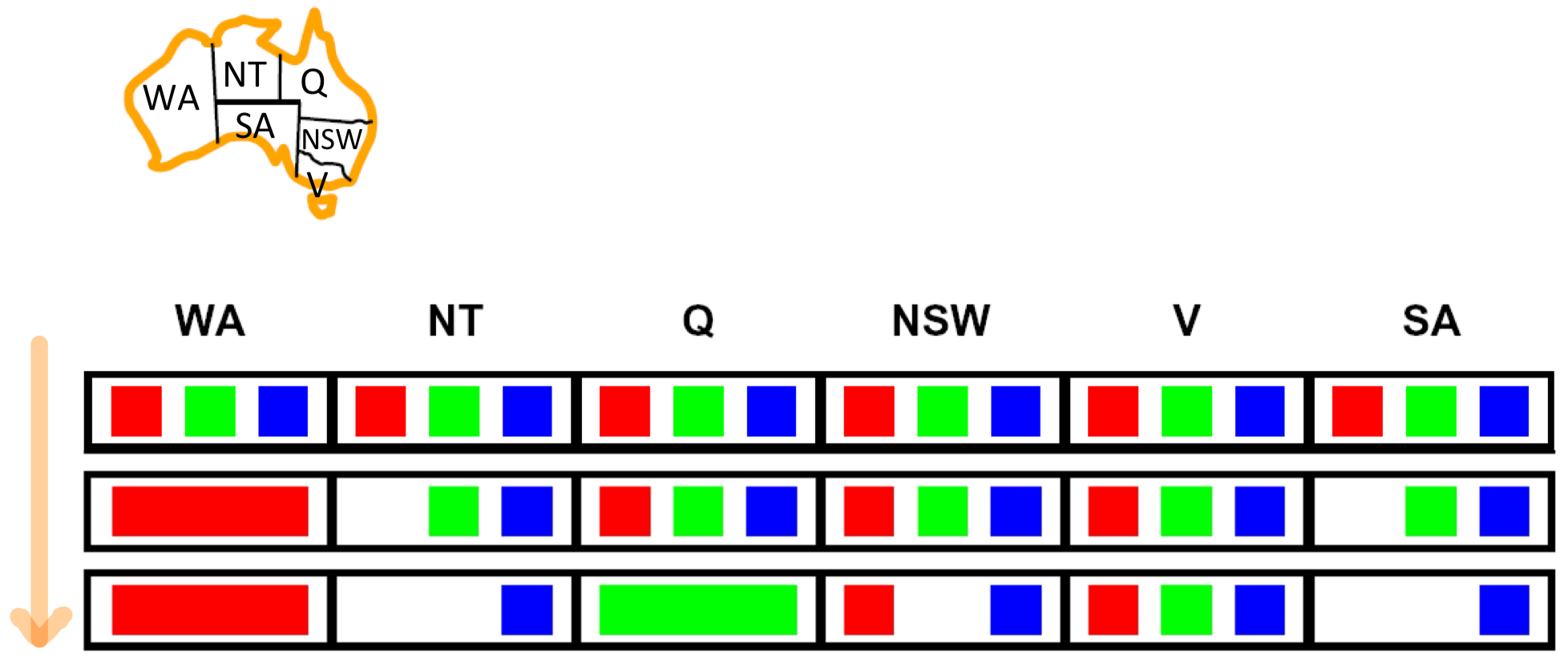
Map Coloring 문제를 예로 들자면, 위와 같은 순서대로 Forward Cheking 을 할 수 있다.
$\text{WA, Q}$에 대해서 각각 값을 할당하고, 할당된 변수와 근접한 변수(영향을 받는)를 확인하는 과정을 보여준다.

다만 위 그림에서 $\text{NT, SA}$에 할당 가능한 값을 보면 2개 변수 모두 $\text{blue}$만을 가지고 있음을 알 수 있다.
이 경우는 해를 구할 수 없는 경우지만, Forward Checking은 할당된 변수와 근접한 변수와의 제약조건, 즉 $\text{NT}\rightarrow\text{Q}, \;\text{SA}\rightarrow\text{Q}$만을 확인하고 $\text{NT}\rightarrow\text{SA}$ 간의 제약조건은 확인하지 않기 때문에 해를 구할 수 없는 경우인지 판단할 수 없다.

위의 예시에서는 $\text{[WA = red then Q = green]}$를 할당했을 때, $SA = \{\}$ 이기 때문에 해를 구할 수 없는 경우임을 알 수 있다.

Constraint Propagation

위의 Forward Checking의 단점을 보완한 것이 Constraint Propagation이다.
Constraint Propagation은 값이 할당된 변수의 근접한 변수만 확인하는 것이 아니라, 제약조건 관계가 있는 모든 변수를 확인하는 방법이다.

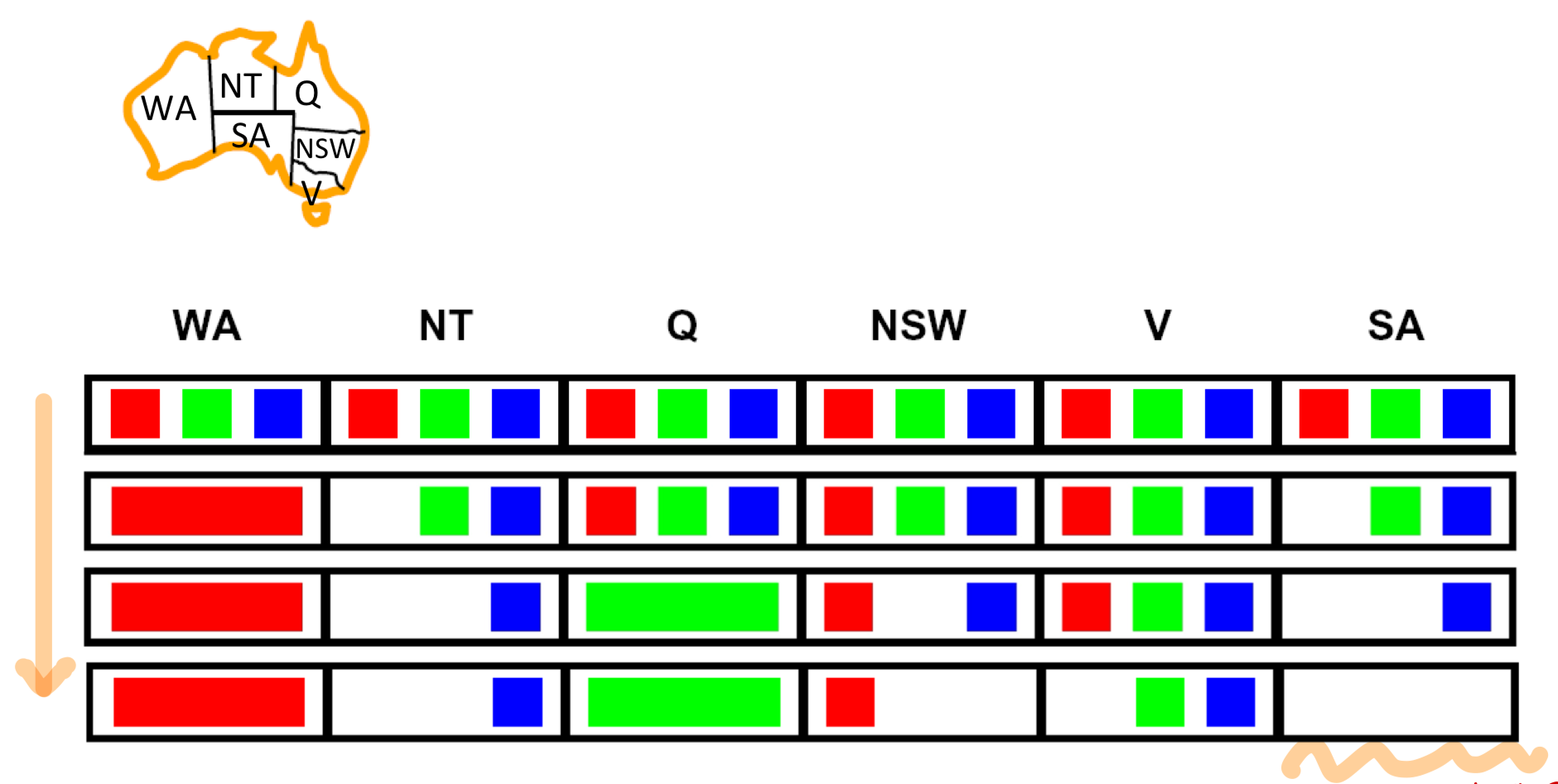
위 그림을 보면, 3번째 단계까지는 Forward Checking과 동일하지만,
Constraing Propagation에서는 $\text{NT}\rightarrow\text{SA}$간의 제약조건까지 확인하여 각 변수에 할당할 수 있는 값을 업데이트함으로써 $\text{Q = green}$ 할당 시에 $\text{SA}$에 이후에 해를 구할 수 없는 경우임을 미리 알 수 있다.

즉, 제약조건 영향을 받은 변수들로부터 제약조건 영향을 받을 변수들까지 확인함으로써 해를 구할 수 없는 Fail Case를 더 빨리 감지 할 수 있다.
이렇게 변수를 확인하는 과정에서 각 변수들의 제약조건들이 충돌하지 않게끔 확인하는 과정은
Consistency(일관성)을 유지하기 위함이라고 말할 수 있다.

K-Consistency

K개 변수 사이에서 Consistency가 만족되는 경우를 말하고,
Consistency에 대한 정의를 일반화 시킨 개념이라고 보면 될 것 같다.

• 1-Consistency (=Node Consistency) : 단일 Node(변수)에 대한 제약조건을 충족하는 경우
• 2-Consistency (=Arc Consistency) : 2개 변수 간에 대한 제약조건을 충족하는 경우
• 3-Consistency (=Path Consistency) : 3개 변수 간에 대한 제약조건을 충족하는 경우
• K-Consistency : K개 변수 간에 대한 제약조건을 충족하는 경우

만약 어떠한 문제가 $1,2,\,\dots\, K$ Consistency를 모두 충족하는 경우 Strong K-Consistency 라고 말한다.

2. Ordering

Ordering은 Variables(변수)에 Value(값)을 할당하는 과정을 효율적으로 하고자 하는 방법이다.
Ordering은 선택하는 대상에 따라서 크게 Variables(변수) / Value(값) 2가지로 분류할 수 있다.
이 2가지에 대한 Ordering 방법을 살펴보자.

1️⃣ Variable Ordering: Minimum remaining values (MRV)
MRV는 어떠한 변수를 선택할지에 대한 방법으로,
MRV는 할당할 수 있는 값(from Domain)이 가장 적게 남은 변수를 선택하는 방법이다.
이를 통해 실패 여부를 빨리 확인함(Fail-fast Ordering)으로써 불필요한 탐색을 줄이고자 함이다.

2️⃣ Value Ordering : Least Constraining Value (LCV)
LCV는 어떠한 값을 할당할지에 대한 방법으로,
값을 할당했을 때 Constraint을 적게 생기게 하는 방향으로 값을 선택하는 방법이다.

3. Structure

Independent Subproblems

만약 1개의 문제에서 독립적인 부분 문제로 나눌 수 있다면, 분리해서 해를 구하는 것이 더 빠르다.
그러나 부분 문제로 나누기 위해서는 문제에 대한 이해도가 많이 필요하다.

Tree-Structured

Constraint graph에서 Loop가 없다면 이는 Tree 구조 형태이고 시간복잡도 $O(nd^2)$로 풀 수 있다.

Tree-Structured CSP는 아래 과정을 거쳐 풀어낼 수 있다.
1️⃣ Topological sort(위상 정렬)
아무 변수를 Root 변수로 지정하고 이를 기준으로 부모-자식 관계를 만들어준다.

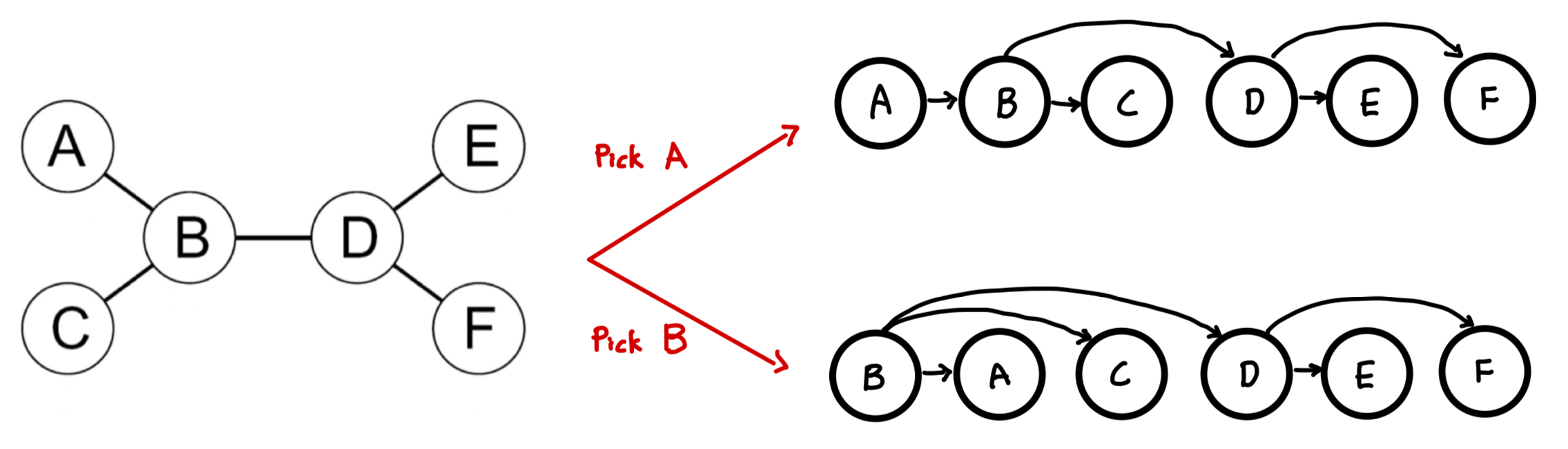
위의 그림은 기존의 Tree에서 각각 A/B를 선택하여 만든 Topological sorted tree이다.
이때의 시간 복잡도는 $O(n)$ 이다.

2️⃣ Remove backward
만들어진 Tree에서 모든 부모→자식 간의 Arc Consistency 를 확인하여 충돌되는 원소를 삭제한다.
아래 그림은 A를 Root 변수로 지정하고, Consistency를 만족하지 못하는 원소를 삭제한 모습이다.

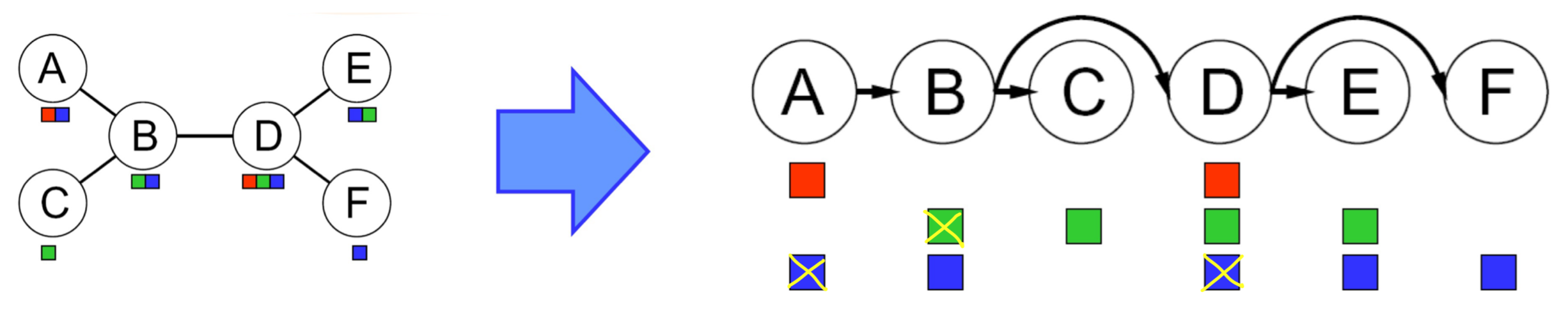
Arc Consistency는 Root 변수(A)를 제외한 모든 변수에 대해서 확인해야하므로
N개의 변수에 대해 d^2(x 변수 내 원소의 개수 * y 변수 내 원소의 개수) 만큼 확인해야 한다.
따라서 시간 복잡도는 $O(nd^2)$이다.

3️⃣ Assign forward
만약 1개의 변수라도 원소를 갖지 못한다면 이는 해가 없음을 의미한다.

그렇지 않고 모든 변수가 Arc Consistency를 만족한다면,
Root 변수의 값이 결정된다면 나머지 변수에 대해서도 값을 할당해줄 수 있다.
이에 대한 시간 복잡도는 $O(n)$이다.

위의 과정들을 통해 Tree-structured 에서 보다 간단하게 해를 구할 수 있고,
전체 과정의 시간 복잡도는 $O(nd^2)$라고 말할 수 있다.

Nearly Tree-Structured

만약 주어진 문제가 Tree-Structured는 아니지만 이에 가까운 구조라면,
이러한 문제를 Tree-Structured로 바꾸어서 해결할 수도 있다.

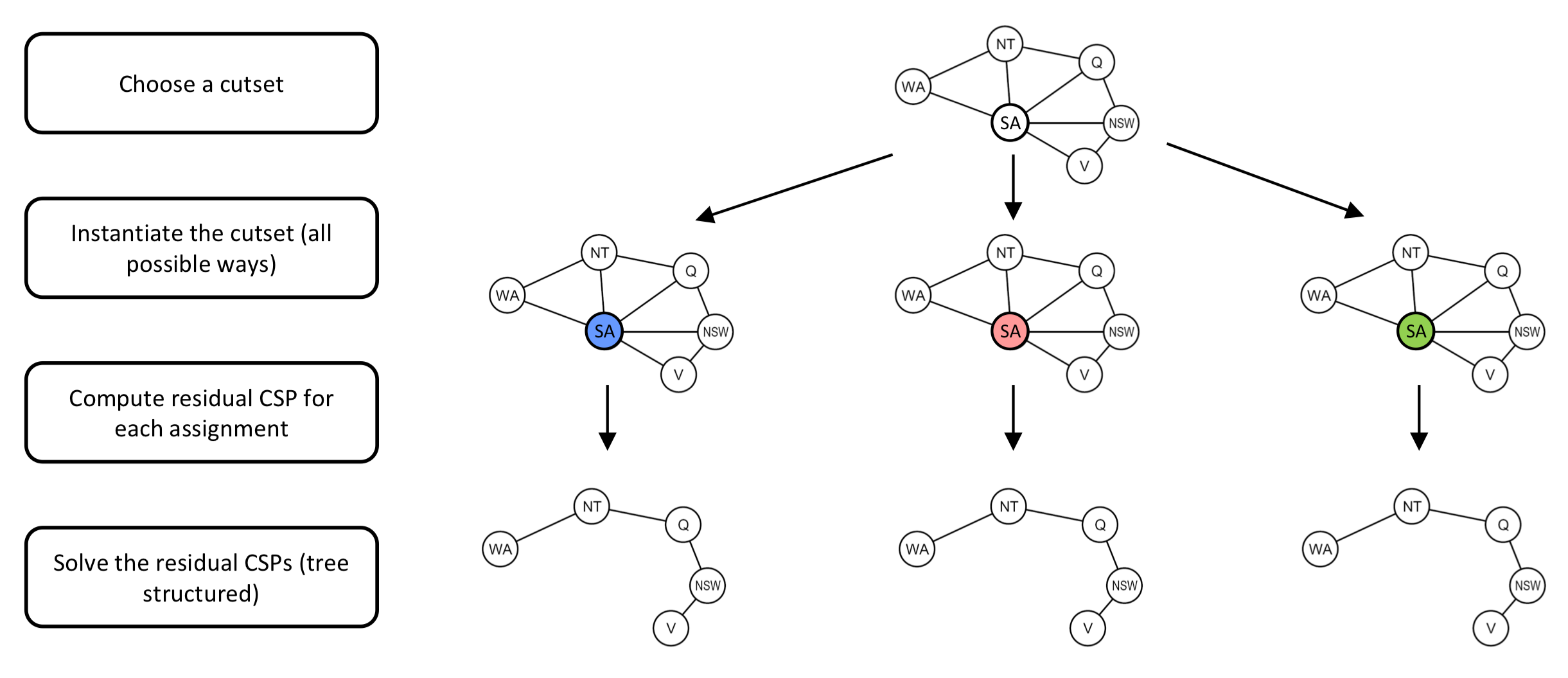
만약 문제에서 존재하지 않는다면 문제를 Tree-Structured로 바꿀 수 있는 특정 변수 Cutset을 찾아내고,
Cutset의 값을 강제적으로 할당한 뒤, Tree-Structured 형태의 문제를 풀면 해를 구할 수 있다.

c = Cutset 개수 / d = 원소 개수일 때, Cutset에 값을 할당하는 경우의 수는 $d^c$
Cutset 변수를 제외한 Tree-Structured 문제 해결의 시간 복잡도는 $O((n-c)d^2)$이기 때문에
전체 시간 복잡도는 $O((d^c)(n-c)d^2)$ 이다.

Tree Decomposition

매우 복잡한 문제를 강제로 부분 문제로 바꾸어 풀어내는 방법이고, 간단하게 설명하면 아래와 같다.
1) 기존 문제를 Tree-Structured 형태의 부분 문제로 분할
2) 부분 문제들을 Tree 형태로 구성
3) 부분 문제로 인해 생기는 제약 조건 추가
4) 각 부분 문제 해결을 통한 기존 문제의 해결

Iterative for CSP

CSP는 경로가 중요한 문제가 아니라 해 그 자체가 중요한 문제이다.
즉, 어떤 과정을 통해서 답을 구했는지가 중요하지 않기 때문에 이전에 다뤘던 반복을 통한 알고리즘인 Local Search를 사용해 볼 수 있다.

Local Search는 Complete state(모든 변수에 값이 할당된 상태)에서 활용하는 방법이기 때문에,
Complete & Satisfies constraints 해를 구하는 CSP 와 일치하는 부분이 있다.

Local Search를 적용한다면 현재 상태와 이웃 상태에 대한 값의 차이를 계산할 수 있어야하는데,
이는 각 상태별 Conflicted variable와 같은 값으로 계산할 수 있고,
값 재할당으로 통해서 현재 상태에서 이웃 상태로 이동 시킬 수 있다.

기존 Search(Uninformed/Informed) ↔︎ Local Search의 차이점은
기존 Search는 값이 할당 되지 않은 상태로부터 탐색을 시작하고,
Local Search는 값이 전부 할당 되어 있는 상태로부터 탐색을 시작한다.

참고 : Performance of Min-Conflicts

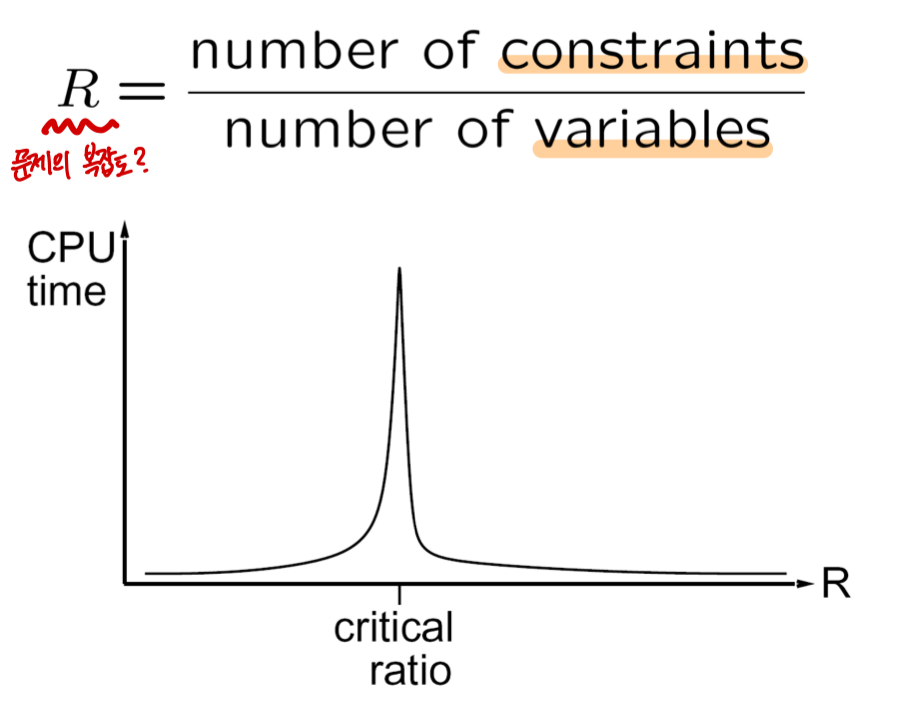
문제의 Constraints가 무수히 많거나, Variables가 무수히 많은 경우 문제는 단순해진다.
하지만 한쪽이 일방적으로 많지 않은 어느 지점(critical ratio)에서는 문제의 복잡도가 급격하게 증가한다.

일반적인 문제들은 Critical ratio 지점의 문제들로써 복잡도가 높은 경향이 있는데,
위에서의 Iterative Method(= Min-Conflicts Algorithm)은 이러한 문제에 대해서
특정 시간 내에서 풀 수 있다는 특징을 지니고 효율적인 경우가 많다.
(ex. N-Queens with n=10,000,000)