기계학습 #5 Neural Network

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

---

이번 글에서는 흔히 딥러닝이라고 불리는 Neural Networks에 대해서 알아보고자 한다.
인간의 뇌세포인 Neuron의 구조를 모방하고 이를 여러겹으로 중첩하여 모델이 가지는 복잡도를 엄청나게 올리는 방법이며, 이를 어떻게 구현하는지 알아보고자 한다.

Perceptron

앞서 말했듯이 Neural Networks 는 Neuron을 모방하여 만들어진 구조이며
1개 Neuron을 모방한 것이 Single Layer Perceptron, 이를 여러겹으로 중첩한 구조를 Multi Layer Perceptron 또는 Neural Networks 이라고 한다.

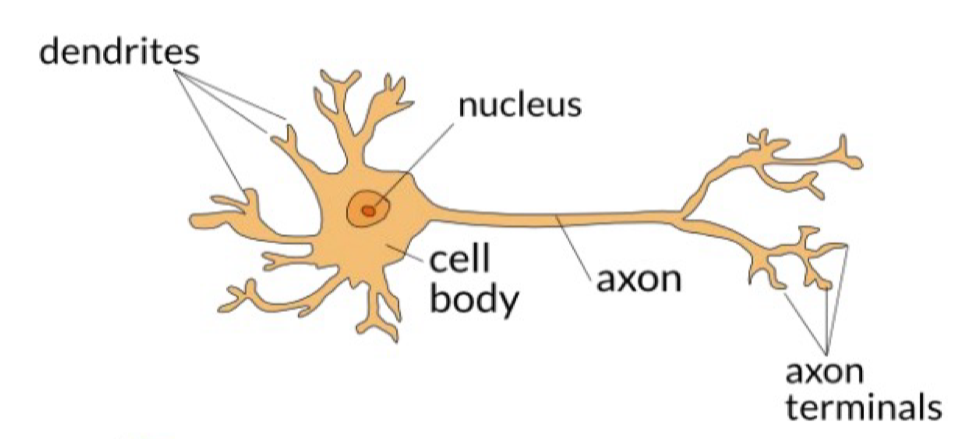
1. Neuron

그럼 먼저 Neuron의 동작 원리에 대해서 알아보자.

뇌세포 Neuron은 ① dendrites를 통해 신호를 받아들이고, dendrites의 굵기에 따라 들어오는 신호의 강도가 달라진다. ② 들어온 신호는 Cell body에 쌓이게 되고, ③ 일정 수준 이상이 되는 경우 axon을 통해 이동하며 신호의 세기가 약해지거나 강해진다. ④ 이렇게 이동한 신호는 axon terminals을 통해 배출되는데, 이는 다른 Neuron의 dendrites와 연결되어 있기 때문에 다른 Neuron으로 전달된다.

2. Single Layer Perceptron

그럼 위의 Neuron을 수식을 통해 나타내보면 어떻게 나타낼 수 있을까? 아래 그림을 살펴보자.

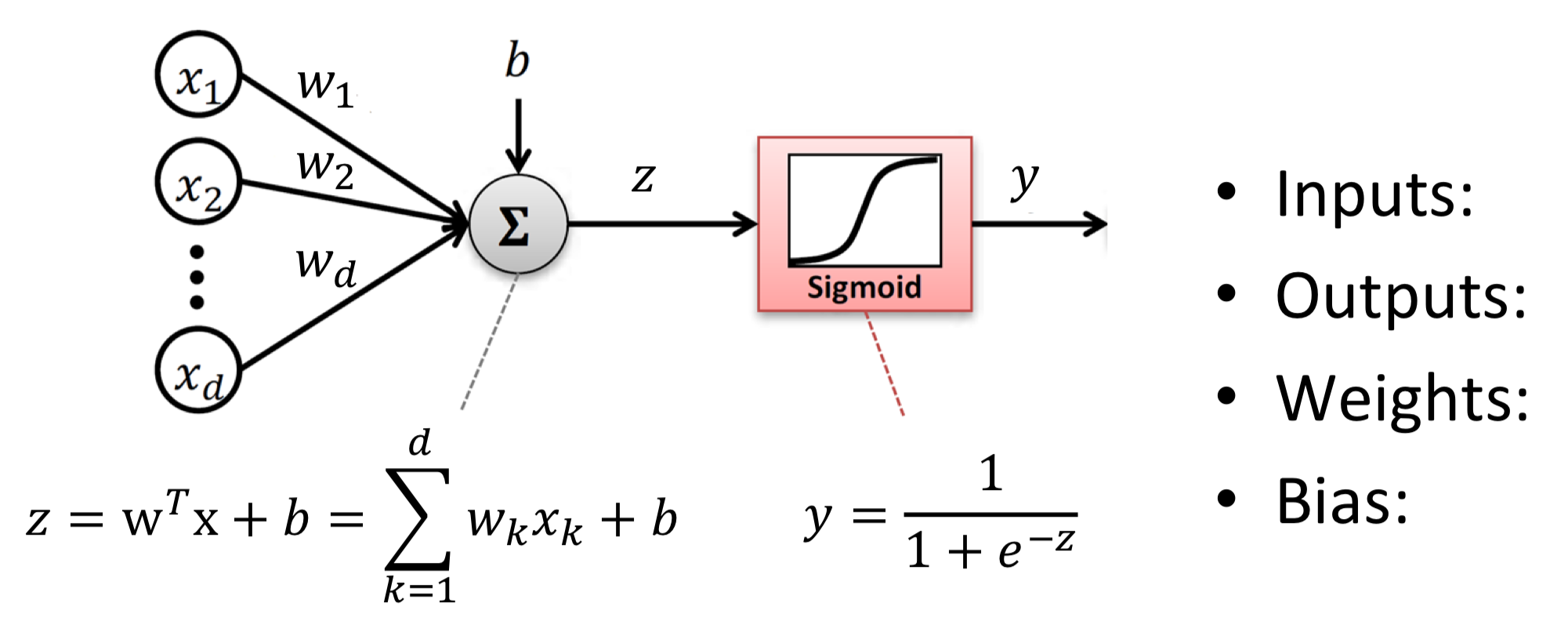
먼저 ① 입력값은 $w$ 를 통해서 각각 입력값의 크기가 조절된 채로 입력된다. ② 그리고 입력 된 신호는 모두 더해지게 되고 $(\Sigma)$, ③ Sigmoid Function 을 통해 0과 1 사이의 값으로 변환된다. ④ 이렇게 변환 된 값은 출력으로 내보내진다.

이렇게 Neuron을 본따 만들어진 구조를 Single Layer Perceptron 이라고 한다.

2. Single Layer Perceptron 한계

다만 Single Layer Perceptron은 한계가 있다.
컴퓨터의 기본적인 논리 연산인 OR, AND, NOT 등의 연산은 계산할 수 있지만,
XOR 연산은 Single Layer Perceptron으로 풀 수 없다는 것이다.

하지만 이러한 문제도 Single Layer Perceptron을 여러개 사용한,
Multi Layer Perceptron 구조를 이용한다면 풀어낼 수 있다.
아래의 그림과 같이 2개 Layer를 가진 Perceptron을 사용한다면, XOR 문제를 포함한 더 복잡한 문제들을 풀어낼 수 있다.

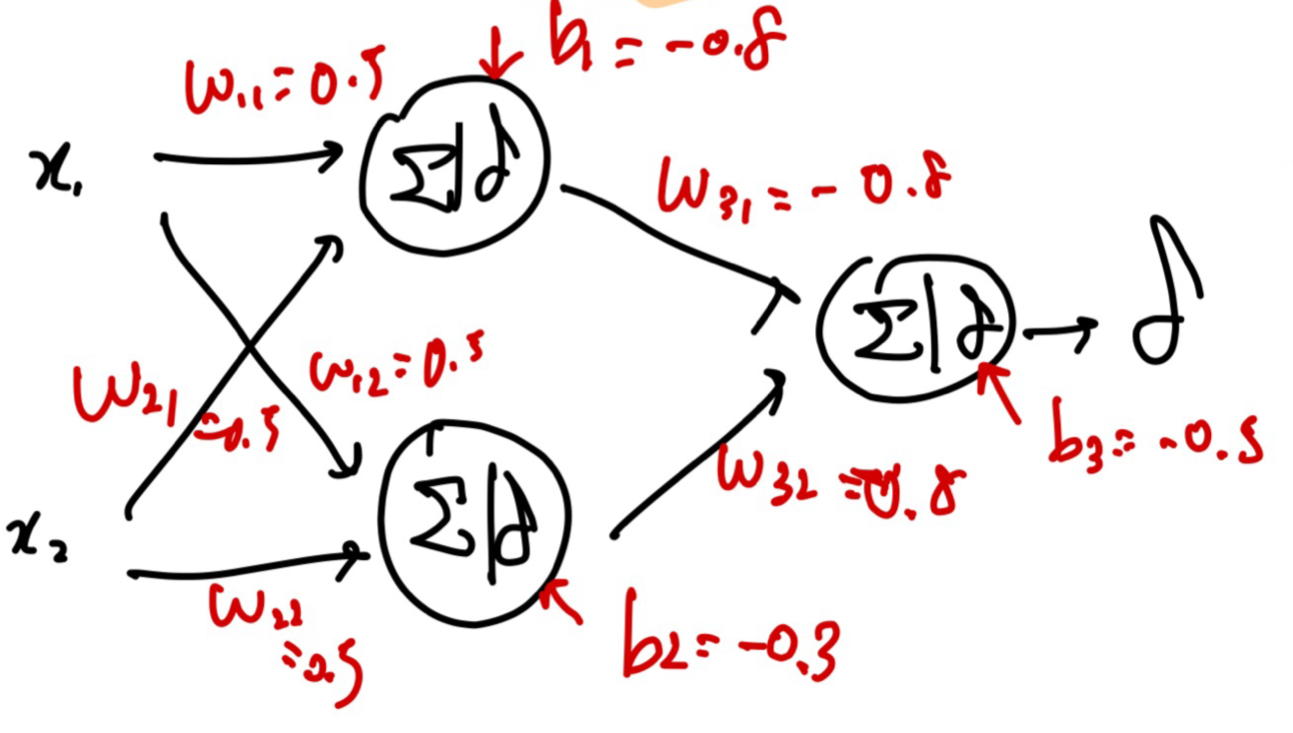
Neural Network

위와 같이 여러개의 Layer를 사용한다면 Multi Layer Perceptron(MLP)라고 하며,
Neural Network, Fully-Connected Networks 이라고도 말한다.
여기서는 주로 쓰이는 명칭인 Neural Network를 사용하겠다.

1. Single ↔︎ Multi Layer

우선 Single Layer ↔︎ Multi Layer는 어떤 차이가 있길래
XOR 문제를 포함한 더 복잡한 문제들을 풀어낼 수 있는지 한번 알아보자.

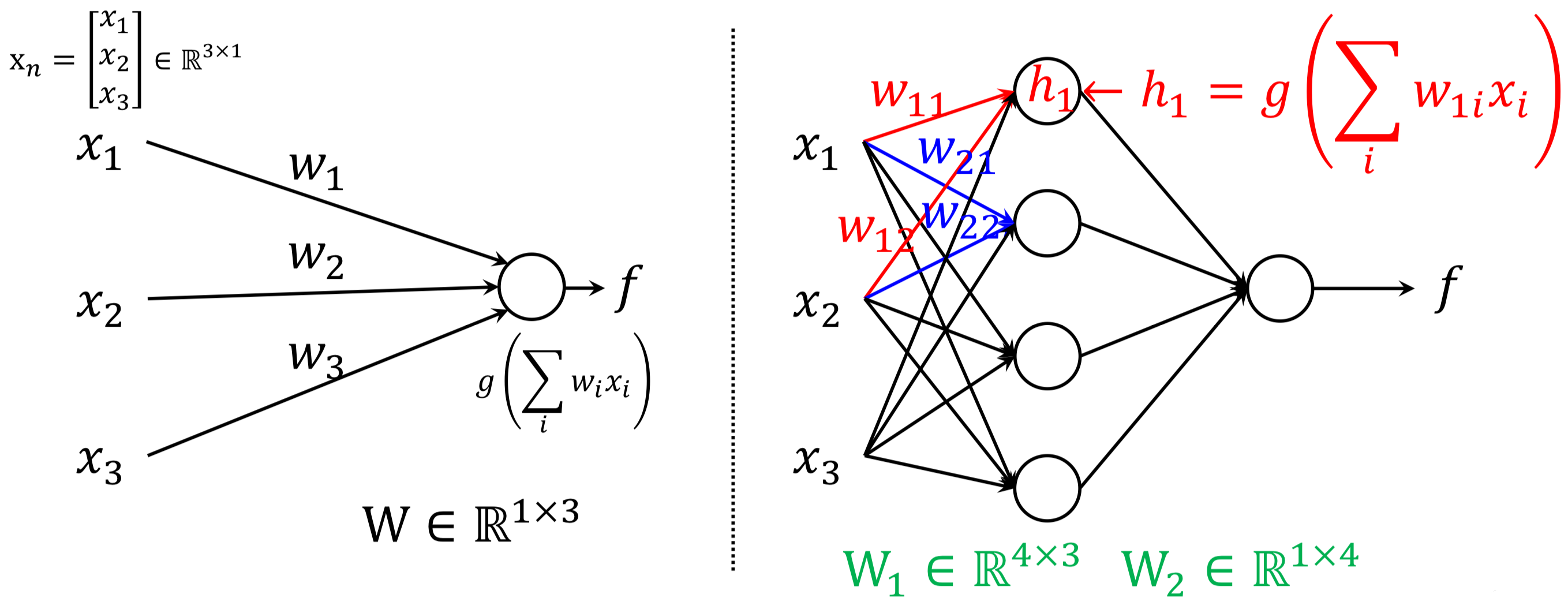
왼쪽은 Single Layer Perceptron, 오른쪽은 2-Layer(Multi) Perceptron 이다.
왼쪽의 Mapping function $f = \text{Wx}_{n} \,\,\text{or} \,\, f = g(\text{Wx}_{n})$ 이고,
오른쪽의 Mapping function $f = \text{W}_{2}g(\text{W}_1\text{x}_{n})$ 이다.

즉, 왼쪽은 1개의 Linear or Logistic Regression을 사용하였고 오른쪽은 2개를 사용한 것을 알 수 있다.
그만큼 더 많은 parameter $w$를 사용하기 때문에 더 복잡한 모델, 더 복잡한 문제를 풀 수 있는 것이다.

2. Neural Network 구조

Neural Network는 기본적으로 아래와 같은 구조를 가지고,
여기에 더 많은 Layer와 Hidder Layer를 중첩시켜 더 복잡한 Neural Network를 만들어낸다.

Input Layer, Output Layer는 각각 입력 / 출력에 대한 층이고
Layer에서는 parameter $w$를 연산, Hidder Layer는 Activation Function(Sigmoid)를 연산한다.

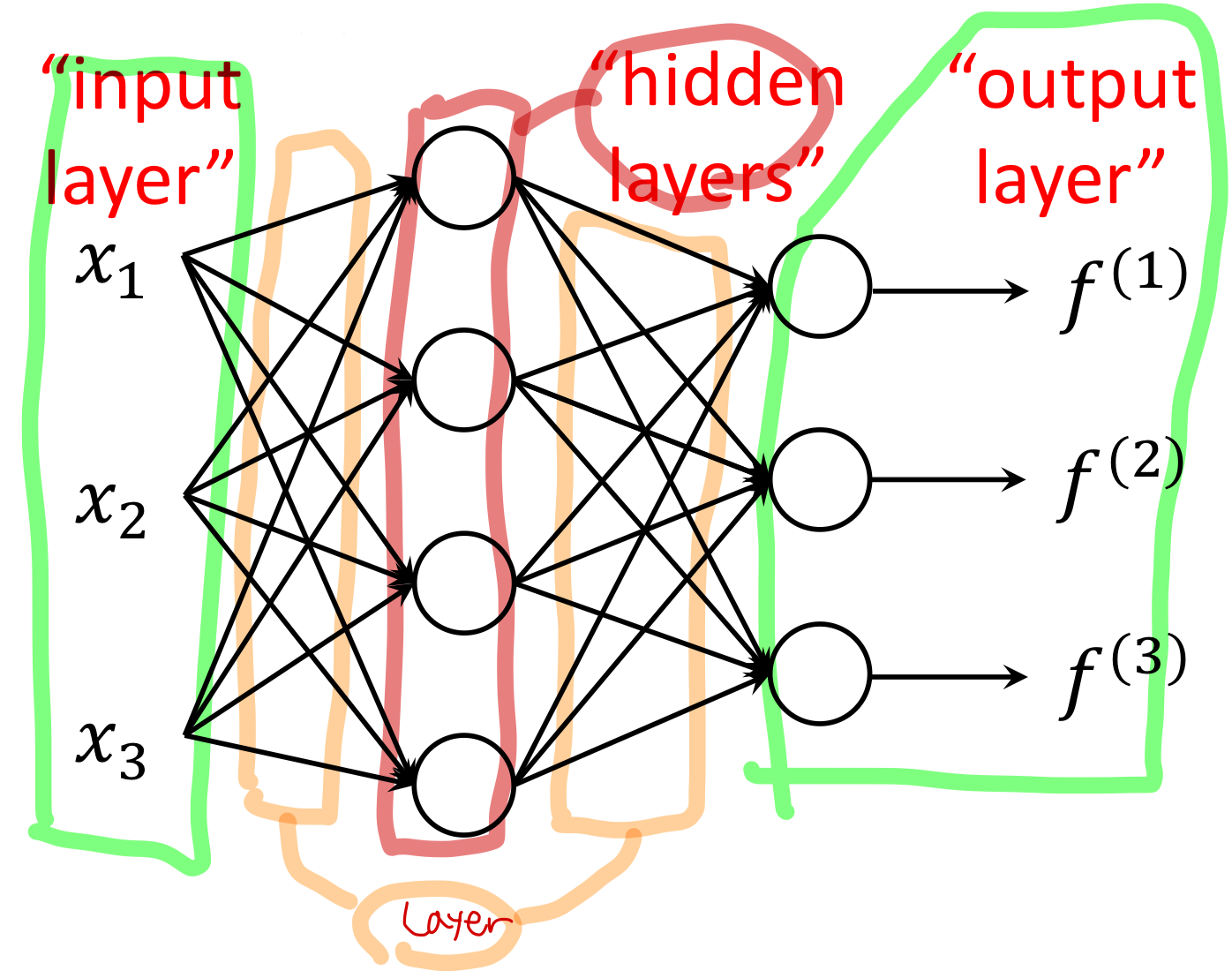
따라서 아래와 같은 구조를 가진 Neural Network는,
3-layer Neural Net 또는 2-hidden-layer Neural Net 이라고 말할 수 있다.

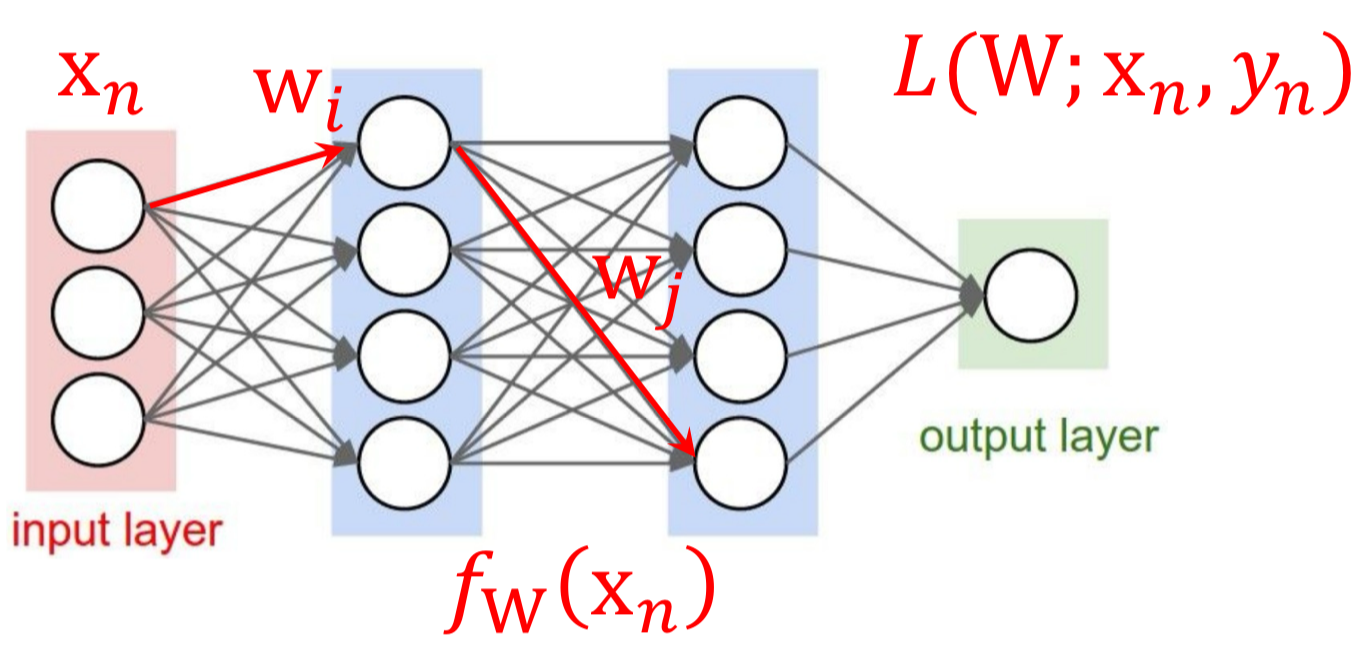
3. Activation Function

Hidden layer에서는 비선형 연산을 실행하게 되며, 이를 Activation Function 이라고 말한다.
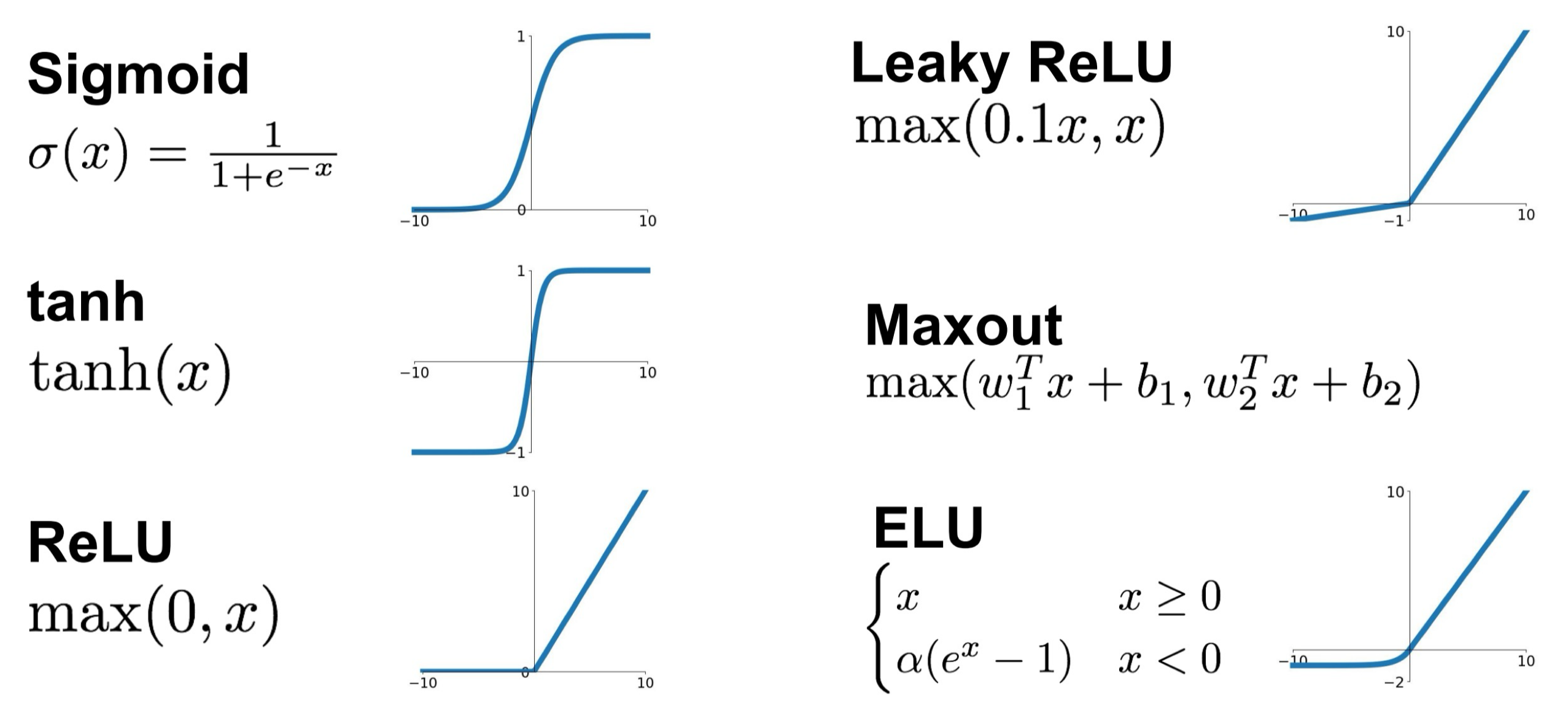
이전에 계속해서 사용해왔던 Activation Function으로는 Sigmoid가 있으며,
아래 그림처럼 여러가지의 Activation Function이 있다.

Neural Network 에서는 이 중 ReLU를 가장 많이 사용하니 참고만 해두자.

Neural Network에서도 이전에 배웠던 Linear Regression과 동일하게 Optimizer로써 Gradient Descent를 사용하여 최적의 w를 찾게 된다. 다만 굉장히 복잡한 모델인 만큼 Gradient를 구하는 과정도 복잡해질 것 같은데, 이에 대한 과정을 다음 글인 Backpropagation에서 다뤄보고자 한다.