기계학습 #6 Backpropagation

Kyeongmin·2024년 5월 3일
0

대학원

목록 보기
12/27

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

앞에서 Linear Regression, Logistic Regression에 대해 다루며 Gradient Descent를 통해 최적의 w를 찾는 과정을 다뤘었다. 이번 글에서는 Neural Network에서의 Gradient Descent 과정에 대해서 다뤄보고자 한다.

Neural Network에서도 Optimizer로 Gradient Descent을 활용한다.
하지만 이전과는 다르게 wiw_i에 대한 기울기를 찾기 위한 과정이 더 복잡해졌다.

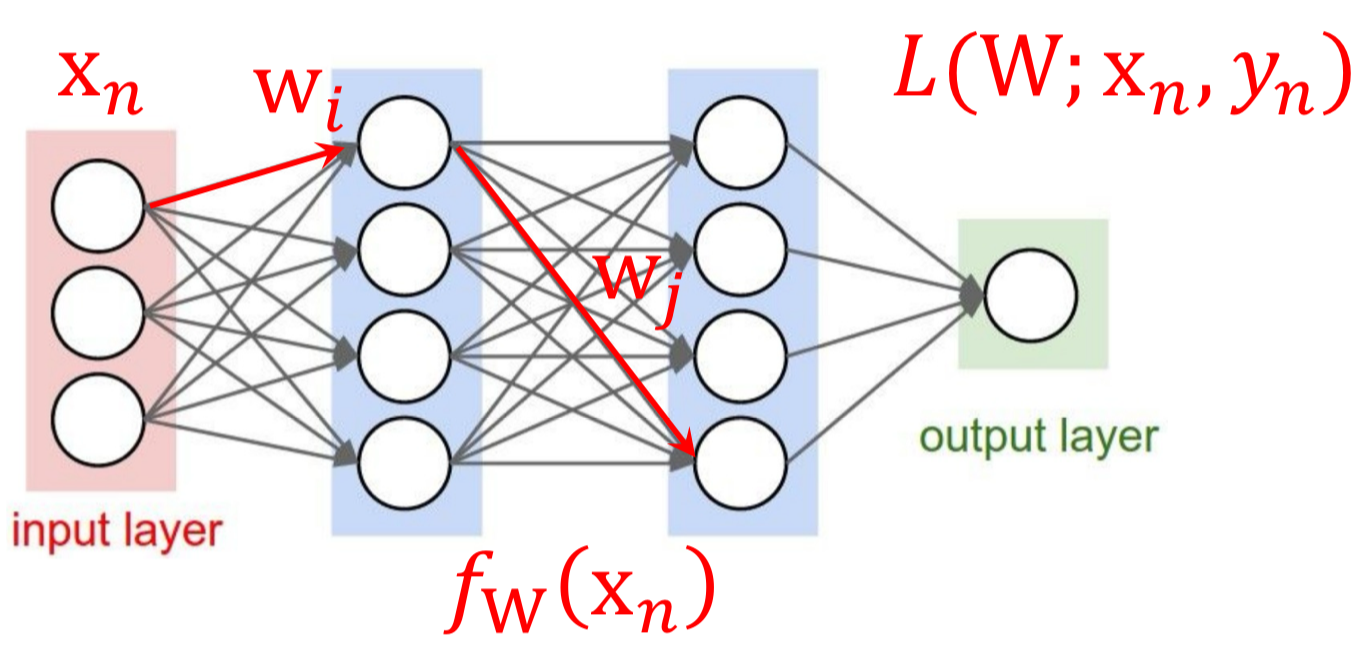
아래의 3-Layer Neural Network에서 wiw_i를 찾기 위해서는
L→Output→Hidden Layer(1)→Hidden Layer(2)→wiL \rightarrow \text{Output} \rightarrow \text{Hidden Layer}_{(1)} \rightarrow \text{Hidden Layer}_{(2)} \rightarrow w_i
4번의 과정을 거쳐야지 구할 수 있다. 여기까지는 어떻게 계산해볼 수 있을 것이다.

하지만 Layer가 더 많이 생긴다면? Hidden Node가 더 많이 생긴다면?
우린 이미지, 자연어 처리 등 더 복잡한 문제를 해결하기 위해 더 복잡한 모델을 만들어야 하는데
여기에 Gradient Descent를 어떻게 적용할 수 있을까?

Computation Graph

먼저 간단한 수식을 Computation Graph를 통해 나타내어 편미분 과정을 계산해보고,
편미분 과정에 대해 이해하는 시간을 가져보자.

Neural Network의 Loss 계산 과정을 Computation Graph로 나타냈을때,
독립인 Graph는 각각의 연산 과정이 다른 연산에 영향을 미치지 않는 것을 뜻한다.
이는 우리가 CPU가 아닌 GPU를 쓰는 이유와 직결된다.
각각의 독립인 연산을 (GPU를 통해) 병렬로 수행함으로써 연산 속도를 높일 수 있기 때문이다.

1️⃣ 수식의 Computation Graph 표현
f(x,y,z)=(x+y)⋅zf(x,y,z) = (x+y) \cdot z에 대한 식을 Computation Graph로 나타내보자.
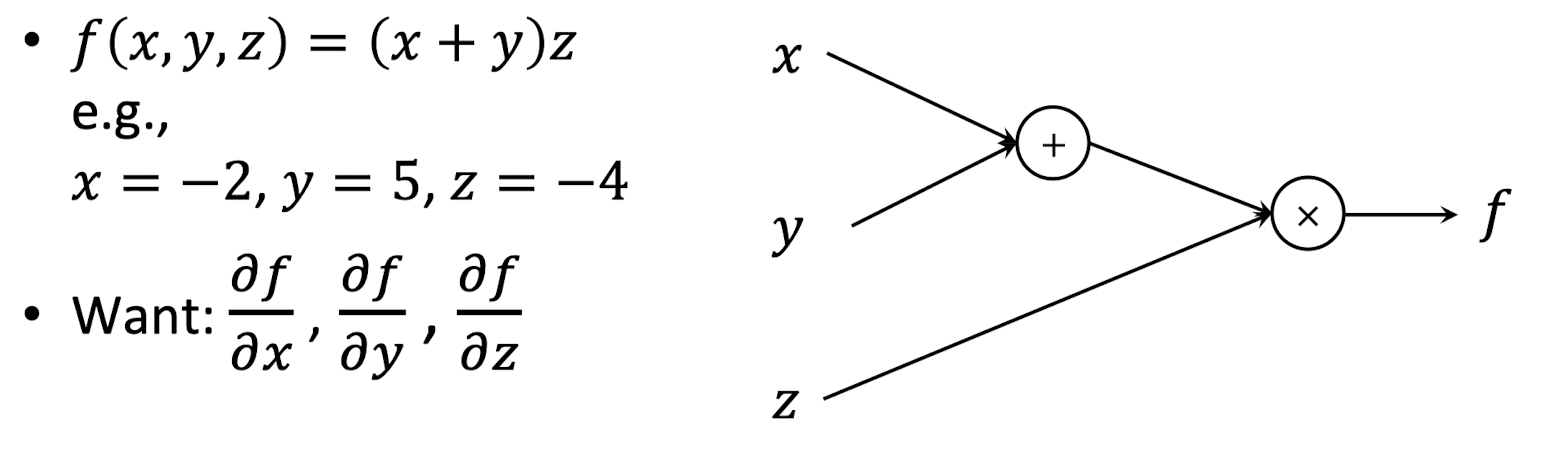
여기에서 우리는 여기에서 출력값에 대한 각 입력값의 기울기를 구해볼 것이다. (∂f∂x,∂f∂y,∂f∂z\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z})

각 Node는 연산이 수행되는 지점인데,
이를 다른 변수로 나타내보면 q=x+y , f=q∗zq= x+y \,,\, f = q*z 와 같이 나타낼 수 있다.

2️⃣ Forward Propagation (Output 계산)
위에서 주어진 입력값(x=−2, y=5, z=−4x=-2,\,y=5,\,z=-4)를 가지고 출력값을 계산해보자.
그럼 q=x+y=3,  f=q∗z=−12q=x+y=3,\;f=q*z=-12 이다.

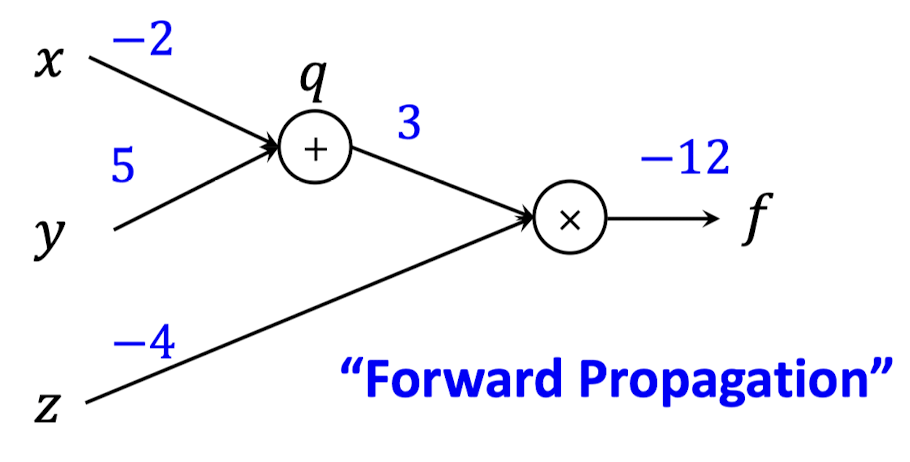
Neural Network의 Computation Graph에서 구해지는 출력값은 Loss 일 것이고,
이를 구하는 과정을 Forward Propagation이라고 말한다.

3️⃣ Backward Propagation (Gradient 계산)
∂f∂x,∂f∂y,∂f∂z\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} 는 Chain Rule에 의해서 아래와 같이 나타낼 수 있다.

∂f∂x=∂f∂f∂f∂q∂q∂x,∂f∂y=∂f∂f∂f∂q∂q∂y,∂f∂z=∂f∂f∂f∂z\frac{\partial f}{\partial x}=\frac{\partial f}{\partial f}\frac{\partial f}{\partial q}\frac{\partial q}{\partial x} \quad,\quad \frac{\partial f}{\partial y}=\frac{\partial f}{\partial f}\frac{\partial f}{\partial q}\frac{\partial q}{\partial y} \quad,\quad \frac{\partial f}{\partial z}=\frac{\partial f}{\partial f}\frac{\partial f}{\partial z}

위 식에서 나온 각각의 편미분은 아래와 같이 계산할 수 있다.

∂f∂f=1 , ∂f∂q=z , ∂f∂z=q , ∂q∂x=1 , ∂q∂y=1 , \frac{\partial f}{\partial f} = 1 \,, \, \frac{\partial f}{\partial q}=z \,, \, \frac{\partial f}{\partial z}=q \,, \, \frac{\partial q}{\partial x}=1 \,, \, \frac{\partial q}{\partial y}=1 \,, \,

각각의 편미분 값을 대입하는 방식으로, 각 입력 변수에 대한 Gradien를 구할 수 있다.

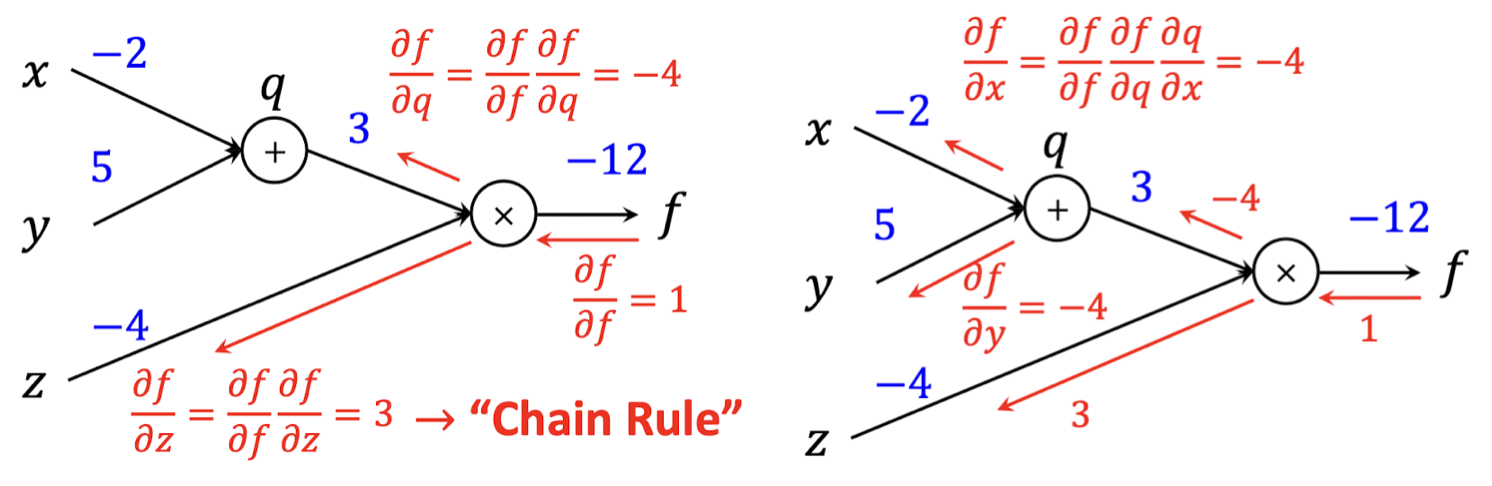
이렇게 Gradient를 계산하는 과정을 정리하자면,
① Output(Loss)을 계산하는 함수를 각 입력 변수에 대한 함수들로 나누고
② 각각의 함수들을 미분한 뒤 곱하여 Output에 대한 입력 변수의 미분값(Gradient)을 구할 수 있다.

Local Gradients

Computation Graph에서 1개 Node를 분리해서 살펴보면 재밌는 특징을 알 수 있다.

아래와 같이 x,wx,w를 입력으로 받고 이에 대한 결과 값이 hh인 func(x,w)\text{func}(x,w)가 있다고 가정해보자.
이는 Neural Network 구조에서 1개의 Hidden Node와도 같다.

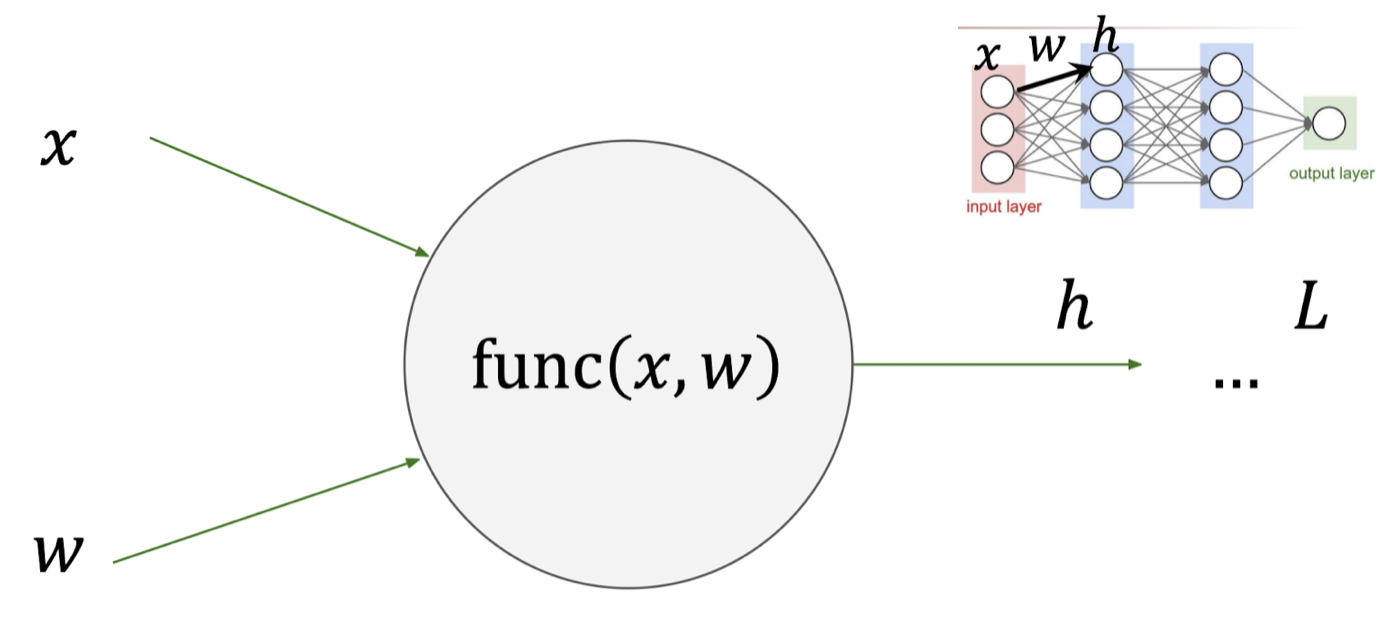
위에서의 Computation Graph를 통한 미분 과정과 동일하게,
최종 출력값 LL 을 입력 x,wx,w에 대하여 미분한 ∂L∂x,∂L∂w\frac{\partial L}{\partial x}, \frac{\partial L}{\partial w} 을 구한다고 가정해보자.

그럼 우리는 Chain Rule을 통하여 아래와 같은 식을 도출해 낼 수 있다.

∂L∂x=∂L∂h∂h∂x,∂L∂w=∂L∂h∂h∂w\frac{\partial L}{\partial x}=\frac{\partial L}{\partial h}\frac{\partial h}{\partial x} \quad,\quad \frac{\partial L}{\partial w}=\frac{\partial L}{\partial h}\frac{\partial h}{\partial w}

이를 Formulation 하면 아래와 같이 나타낼 수 있다.

∂ Loss∂ input of function=∂ Loss∂ output of function∂ output of function∂ input of function Downstream Gradient=Upstream Gradient⋅Local Gradients\begin{aligned} \frac{\partial \text{ Loss}}{\partial \text{ input of function}}&= \frac{\partial \text{ Loss}}{\partial \text{ output of function}} \frac{\partial \text{ output of function}}{\partial \text{ input of function}} \\\,\\ \text{Downstream Gradient}&=\text{Upstream Gradient} \cdot \text{Local Gradients} \end{aligned}

여기서 중요한 점은, Downstream Gradient는 이전 Node의 Upstream Gradient이라는 것이다.
우리는 i번째 Node의 입력인 wiw_i에 대한 Gradient를 구해야하고, 이를 Formulation 하면 아래와 같다.

Downstream Gradient(i)=Local Gradient(i)⋅Local Gradient(i+1)⋯Local Gradient(M)\scriptsize\text{Downstream Gradient}_{(i)} = \text{Local Gradient}_{(i)}\cdot \text{Local Gradient}_{(i+1)}\,\cdots\,\text{Local Gradient}_{(M)}

여기서 Upstream Gradient를 곱하지 않는 이유는,
가장 마지막 Node의 Upstream Gradient를 생각해보면 함수의 출력값 = 최종 출력값이기 때문에
마지막 Node의 Upstream Gradient는 스스로를 미분하는 꼴이므로 1 이 나오게 된다.
그렇게 때문에 위 수식에서 Upstream Gradient는 생략되는 것이다.

결론은 우리가 찾고자 하는 Gradient는,
각 Function에 대한 Local Gradient를 구하고 곱함으로써 계산할 수 있다는 것이다.

Update Parameters

이제 Local Gradient를 이용한 Backpropagation을 통하여 Parameter를 찾는 과정을 한번 살펴보자.

1. Vector Derivatives

그 전에 먼저 Vector 간의 미분은 어떻게 이뤄지는지 먼저 알아보고자 한다.

1) Scalar to Scalar

2개 변수 모두 Scalar인 경우에는 우리가 기존에 알고 있는 미분과 동일하다.
미분의 결과 또한 Scalar 일 것이다.

x∈R  ,  y∈R⇒∂y∂x∈Rx \in \mathbb{R} \;,\; y \in \mathbb{R} \quad \Rightarrow \quad \frac{\partial y}{\partial x}\in\mathbb{R}

2) Vector to Scalar

하지만 Scalar를 Vector로 미분하는 경우는 미분의 결과값이 Scalar가 아니게 된다.
아래와 같이 분자(Vector)의 Size를 Row Vector로 가지게 된다.
이를 보통 Gradient라고 명칭한다.

x∈RN  ,  y∈R⇒∂y∂x∈RN  ,  (∂y∂x)n=∂y∂xn\text{x} \in \mathbb{R}^{N} \;,\; y \in \mathbb{R} \quad \Rightarrow \quad \frac{\partial y}{\partial \text{x}}\in\mathbb{R}^{N} \;,\; \biggl( \frac{\partial y}{\partial \text{x}} \biggl)_n = \frac{\partial y}{\partial \text{x}_n}

3) Vector to Vector

그럼 Vector를 Vector로 미분하는 경우는 어떨까?
분자(Vector)의 Size를 Row Vector로, 분모(Vector)의 Size를 Column Vector로 가지게 된다.
이를 Jacobian이라고 명칭한다.

x∈RN  ,  y∈RM⇒∂y∂x∈RN×M  ,  (∂y∂x)n,m=∂ym∂xn\text{x} \in \mathbb{R}^{N} \;,\; \text{y} \in \mathbb{R}^{M} \quad \Rightarrow \quad \frac{\partial \text{y}}{\partial \text{x}}\in\mathbb{R}^{N \times M} \;,\; \biggl( \frac{\partial \text{y}}{\partial \text{x}} \biggl)_{n,m} = \frac{\partial \text{y}_m}{\partial \text{x}_n}

※ 분자우선표기 vs 분모우선표기

위에서 다룬 Scalar to Scalar 미분 외에, Vector를 통한 미분은 차원이 들어가게 되어 헷갈릴 수 있다.
위에서는 분자 Size → Row Vector, 분모 Size → Column Vector로 나타내었는데
사실 일관되게만 표기한다면 반대로 표기하여도(분자 Size → Column Vector, 분모 Size → Row Vector) 무방하다.

미분할때 분자를 우선할 것이냐, 분모를 우선할 것이냐에 대한 차이이기 때문인데,
위에서는 분자우선표기(Numerator layout, Jacobian formulation)를 사용한 것이고 이와 반대 개념으로 분모우선표기(Denominator layout, Hessian formulation)이 있다.
(자세한 개념은 위키피디아 참조)

여기(Neural Network)에서 분자우선표기를 사용하는 이유는,
Backpropagation 과정에서 Loss에 대한 w의 미분을 구하고 이를 현재의 w 값에 더해줄 때,
별도의 Transpose를 해주지 않아도 되기 때문이다.
(분자우선표기를 사용하면 분모가 Scalar, 분자가 Vetor 또는 Matrix 일 때, 미분값은 분자의 크기를 따라가게 된다.)

아래와 같은 Neural Network 구조에서 모든 연산을 각각 구분하여 Computation Graph를 그리고 Backpropagation 과정을 표현하면 너무 복잡하기 때문에 다음으로 이어질 Update parameter에서는 Vector, Matrix 를 이용하여 미분 과정을 나타낼 것이다.

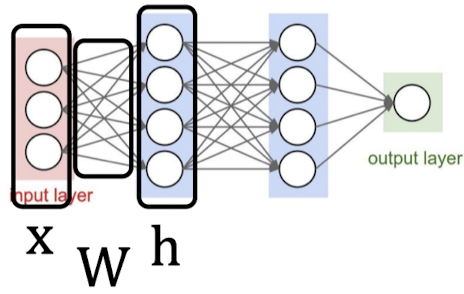
또한 Backpropagation 과정은 결국 행렬곱의 연속인데, 행렬곱 결과의 각 원소는 독립적으로 연산이 수행된다는 특징이 있다. 즉, 각 원소의 값이 서로에게 영향을 미치지 않는다는 점이다. 이는 Neural Network 연산에서 CPU 보다 GPU를 많이 사용하는 이유와 연관되어 있다. 모든 연산을 GPU를 통해 병렬 수행하게 된다면 시간 단축을 훨씬 더 많이 시킬 수 있다.

2. 1-Layer NN with MSE

그럼 이제 1-Layer Neural Network 구조에서 Gradient를 한번 구해보자.

아래 그림에서 각각의 Output Node에서는 아래의 연산이 이루어진다고 가정한다.
① Linear projection : z = Wx + b\text{z = Wx + b}
② Activation function : p = g(z) = 11+exp(-z)\text{p = g(z) = }\frac{1}{1+\text{exp(-z)}}
③ Loss function : L = ∣∣y - p∣∣2\text{L = }||\text{y - p}||^2
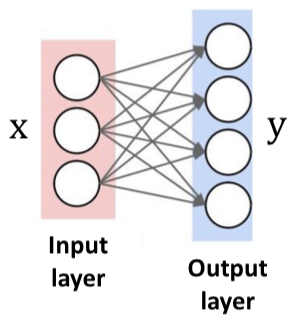
(x∈RD×1 , y∈RM×1 , W∈RM×D , b∈RM×1)\bigl( x\in\mathbb{R}^{D\times 1} \,,\, y\in\mathbb{R}^{M\times 1} \,,\, \text{W}\in\mathbb{R}^{M\times D} \,,\, b\in\mathbb{R}^{M\times 1} \bigl)

1️⃣ Compuatation Graph
위의 내용을 가지고 Computation Graph를 그리면 아래와 같이 그릴 수 있다.

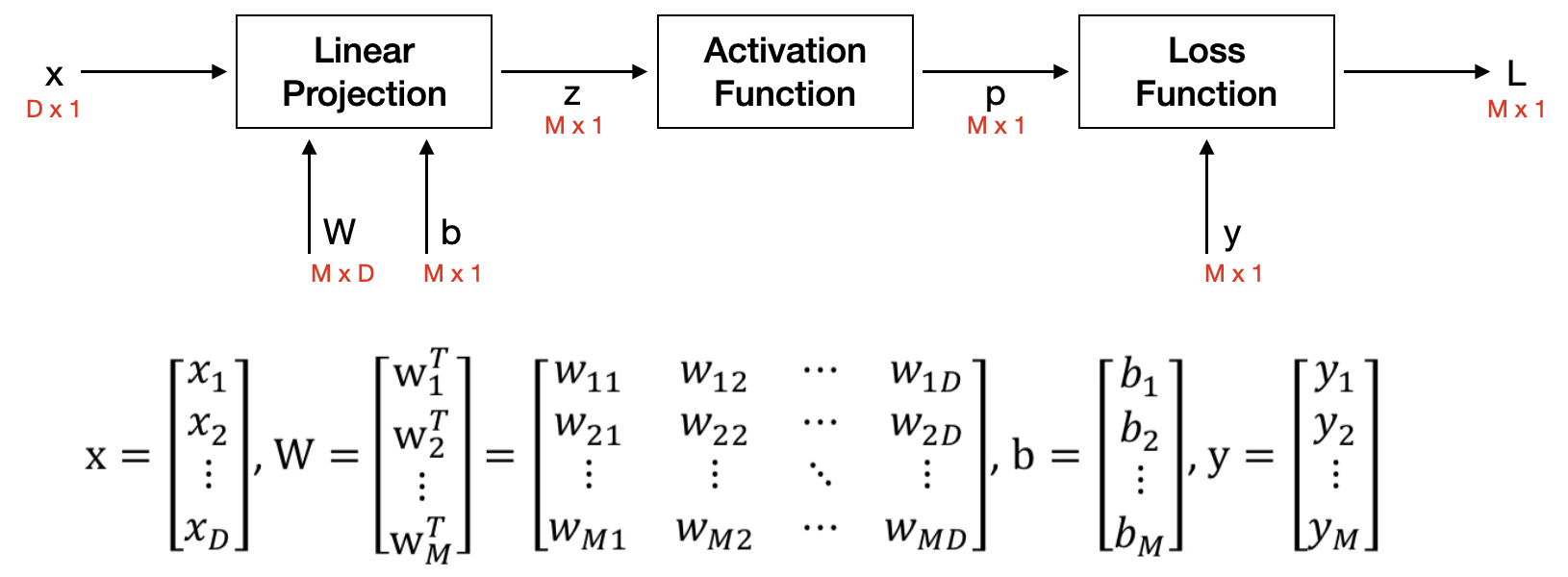
2️⃣ Local Gradient
위에서 Computation Graph의 Function마다의 Local Gradient를 구해보자.
(Loss를 계산하는 Forwardpropagation 과정은 생략한다.)

① Linear Projection

∂z∂w1=[x0⋯0]∈RD×M ∂z∂b=[1⋯0⋮⋮0⋯1]∈RM×M=IM\begin{aligned} \frac{\partial z}{\partial \text{w}_1} &= \begin{bmatrix} \text{x} & 0 & \cdots & 0 \end{bmatrix} \in \mathbb{R}^{D \times M} \\\,\\ \frac{\partial z}{\partial b} &= \begin{bmatrix} 1 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & 1 \\ \end{bmatrix} \in \mathbb{R}^{M \times M}= I_M \end{aligned}

② Activation Function

∂p∂z=∂g(z)∂z=diag((1−g(zi)g(zi))∈RM×M\frac{\partial p}{\partial z} = \frac{\partial g(z)}{\partial z} = \text{diag}((1-g(z_i)g(z_i)) \in \mathbb{R}^{M \times M}

③ Loss Function

∂L∂p=2(p−y)\frac{\partial L}{\partial p} = 2(p-y)

3️⃣ Update w,b
그럼 이제 위에서 구한 Local Gradient를 토대로 우리가 찾고자 하는 w,b를 업데이트 해보자.

∂L∂z=∂p∂z∂L∂p=diag((1−g(zi)g(zi))∂L∂p ∂L∂W=[∂L∂w1⋯∂L∂wM]T=[(∂L∂z)1x⋯(∂L∂z)Mx]T=∂L∂zxT ∂L∂b=∂z∂b∂L∂z=IM∂L∂z=∂L∂z\begin{aligned} \frac{\partial L}{\partial z} &= \frac{\partial p}{\partial z}\frac{\partial L}{\partial p} = \text{diag}((1-g(z_i)g(z_i))\frac{\partial L}{\partial p} \\\,\\ \frac{\partial L}{\partial \text{W}} &= \begin{bmatrix} \frac{\partial L}{\partial \text{w}_1} & \cdots & \frac{\partial L}{\partial \text{w}_M} \end{bmatrix}^{\text{T}} = \begin{bmatrix} \bigl(\frac{\partial L}{\partial \text{z}}\bigl)_1 \text{x}& \cdots & \bigl(\frac{\partial L}{\partial \text{z}}\bigl)_M \text{x} \end{bmatrix}^{\text{T}} = \frac{\partial L}{\partial \text{z}}\text{x}^T \\\,\\ \frac{\partial L}{\partial \text{b}} &= \frac{\partial z}{\partial \text{b}} \frac{\partial L}{\partial z} = I_M\frac{\partial L}{\partial z} = \frac{\partial L}{\partial z} \end{aligned}
profile
Kyeongmin
개발자가 되고 싶은 공장장이🛠
이전 포스트

기계학습 #5 Neural Network

다음 포스트

기초인공지능 #7 Markov Decision Process

0개의 댓글

관련 채용 정보