기초인공지능 #7 Markov Decision Process

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.

---

Uncertain outcomes

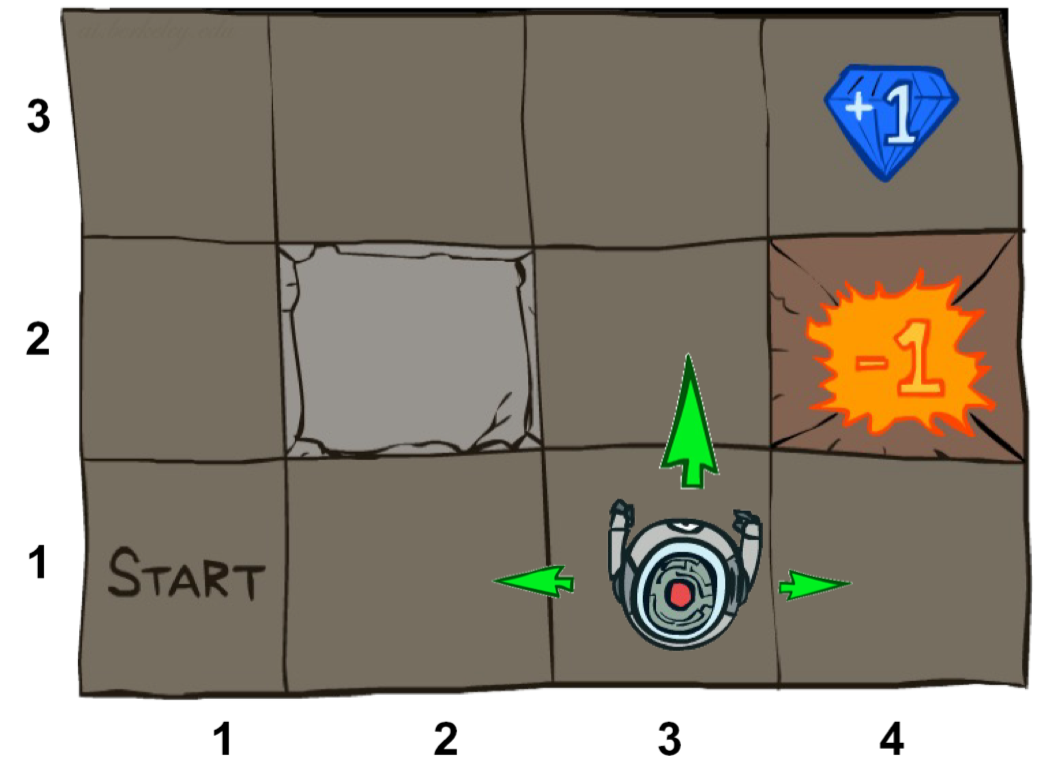
Uncertain outcomes이란, 특정 행동이 특정한 결과를 보장하지 않고 여러 가능한 결과를 낳을 수 있는 상황을 다루는 문제를 말한다. 예를 들어, 로봇이 움직일 때 장애물 또는 다른 문제로 인해 실제 도착지와 예상했던 도착지가 다른 경우를 Uncertain outcomes 라고 볼 수 있다.

Non-Deterministic Search

Certain outcome / Uncertain outcome을 다루는 탐색 문제는 각각
Deterministic / Non-Deterministic(≈Stochastic) Problem이라고 각각 말할 수 있다.

아래 Grid world라는 문제에 대해서 위의 2가지 경우를 가정해보자면,

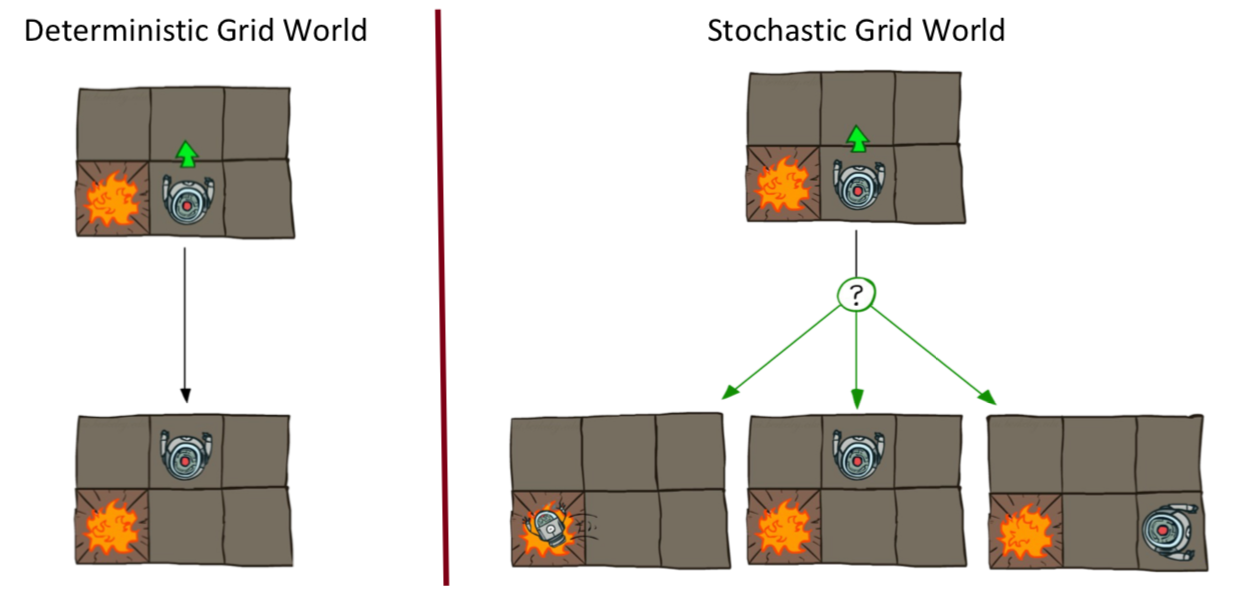
Deterministic grid world에서는 행동에 대한 결과가 보장되어 있으니 최적해를 구하기 위한 행동의 순서를 구할 수 있고 이는 Planning 기법을 통해 풀어낼 수 있다.
하지만 Non-Deterministic grid world에서는 행동에 대한 결과가 매번 달라질 수 있기 때문에 시작 지점부터 최적해까지의 행동의 순서를 구할 수 없다. 따라서 각 State에서 최선의 행동을 찾아내는 Policy를 찾는 것이 목표이다.

Non-Deterministic Search

Non-Deterministic Search의 특징을 아래와 같이 정리할 수 있다.

• Nosiy movement : Action에 대한 결과(Next state)가 보장되지 않는다.
• Rewards each time step : 각 Step마다 Reward를 받는다.
  (오래 살아있을수록 패널티를 받게끔 living reward , negative reward를 설정할 수 있다.)

Markov Decision Process

서론이 조금 길었는데, Uncertain outcomes와 이를 다루는 Non-Detrministic search에 대해서 자세히 설명한 이유는 바로 Markov Decision Process(이하 MDP)가 이러한 문제를 풀기 위한 방법이기 때문이다.

1. 정의

먼저 MDP는 아래 구성요소들을 통해 정의할 수 있다.

• $\text{states }s \in S,\;\; \text{actions }a \in A$
• $\text{transition function }T(s,a,s')$
  • $s$에서 $s'$로 가게 되는 확률 = $P(s'|s,a)$
• $\text{reward function }R(s,a,s')\,\text{or}\,R(s)$
  • $R(s,a,s')$ : State/Action에 따라 Reward 결정, $s$에서 $a$ 행동을 통해 $s'$로 이동했을 때
  • $R(s)$ : State에 따라 Reward 결정, $s$로 이동했을 때
• $\text{start / terminal state}$
• $\text{Policy}\,\pi^* : S\rightarrow A$
  • 각 State마다 Utility(All Reward)를 최대화하는 Optimal action을 제공한다.

MDP는 이전에 다뤘던 Expectimax search와 유사한 방법으로,
각 State에서 행동에 대한 확률들은(Transition Function) 알고 있다고 가정한채로 문제를 풀이한다.

2. MDP Search Tree

MDP의 Search Tree를 그려보면 아래와 같다.
Expectimax Search Tree는 State → Chance Node → State 순으로 진행되는데
MDP Search Tree는 State → Q-State → State 순으로 진행되는 것을 알 수 있다.

그리고 State → Q-State는 Deterministic이고,
Q-State → State는 Non-Deterministic(Stochastic)으로 Transition function에 의해 확률이 구해진다.

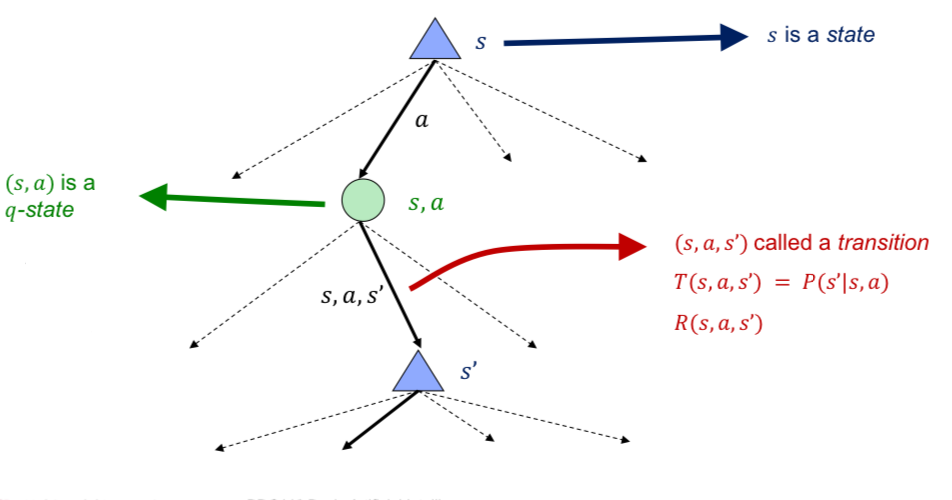
Q-State

여기서 Q-State는 특정 상태 $s$에서 특정 행동 $a$를 취했을 때 기대할 수 있는 Rewards의 총합을 의미한다.
이는 기댓값(다음에 올 수 있는 각 상태들의 Rewards와 각 확률의 곱)을 통해 구할 수 있다.
Expectimax Search의 Chance Node와 동일한 역할이라고 볼 수 있다.

3. MDP의 문제점

1) Utilities of Sequences

이는 Utilities($\approx$Rewards)를 얻게 될 때 어떤 순서로 얻는 것이 좋을지에 대한 문제이다.
예를 들어, 큰 Utility를 먼저 얻는게 좋은지 / 나중에 Utility를 얻는 것이 좋은지 결정하는 문제가 있다.

➡️ Discounting
Maximize utilities 문제에서 합리적으로 판단했을 때 큰 Utility + 지금 Utility 를 얻는 것이 좋을 것이다.
이를 해결하기 위해서 utility 값을 decay exponentially 하는 방법이 있다.

이는 자연스럽게 Algorithm이 큰 Utility를 보다 먼저 얻게 할 것이고, 우리가 원하는 바와 같다.
뒤에서 언급하겠지만 이는 Algorithm Converge 할 수 있도록 한다.

2) Infinite Utilities

만약 게임이 끝나지 않는다면 어떻게 될까? 우리는 무한하게 Utility를 얻게 되는걸까?
이를 방지하기 위해 아래와 같은 해결방안들을 이용할 수 있다.

➡️ Finite horizon
Depth-limited search와 유사한 방법으로, Tree를 확장할 수 있는 최대 깊이를 정해두는 것이다.
이를 통해서 Policy를 구할 순 있지만 Policy가 최대 깊이를 얼마로 설정해두냐에 의존된다는 문제가 있다.

➡️ Discounting $(0 < \gamma < 1)$
Discounting은 Infinite Utilities 문제를 해결하는데 도움을 줄 수 있다.
Step이 반복될수록 Utility 감소되기 때문에 결국 Utilities의 합은 어느 지점으로 수렴하게 될 것이다.
여기서 $\gamma$가 작은 값이라면, Finite horizon에서 최대 깊이를 작게 한 것과 유사한 기능을 한다.

➡️ Absorbing state
게임은 끝나지 않지만, 알고리즘을 수행할 때 특정 지점을 Terminal State,
즉 종료 조건을 강제로 지정해줌으로써 유한한 Utilities를 보장하고 Policy를 찾을 수 있다.

Optimal Quantities

MDP에는 아래와 같은 값들이 있고 이에 대한 최적의 값을 찾음으로써 문제를 해결할 수 있다.

• $V^*$ : 상태 $s$에서 최적의 행동들을 수행했을 때 기대되는 Utility 값
• $Q^*(s,a)$ : 상태 $s$에서 행동 $a$를 수행하고 이후 최적의 행동들을 수행했을 때 기대되는 Utility 값
• $\pi^*(s)$ : 상태 $s$에서의 최적의 행동 $a$

1. Bellman Equations(벨만 방정식)

Bellman Equations은 MDP에서 최적의 정책을 찾기 위한 방정식이며,
현재 상태 $s$와 다음 상태 $s'$ 간의 관계를 통해 Optimal Quantities를 나타낸다.
$V^*, \; Q^*(s,a)$를 Bellman Equations을 통해 나타내면 아래와 같다.

위 수식에서 $\gamma V^*$은 이후의 보상에 Discounting을 적용한 것을 의미한다.
또한 위의 식을 정리하면 아래와 같이 표현할 수 있다.

Bellman Equations에서 각각의 값은 현재 상태와 다음 상태 간의 관계$\big(V^*(s) \leftrightarrow V^*(s')\big)$
즉, 재귀적으로 표현되기 때문에 계산할 수 있지만 여기에 몇가지 문제점이 있다.

2. Optimal Quantities의 계산

Bellman Equatitions를 가지고 재귀적으로 계산을 하게 되면,
상태가 반복되는 Cycle이 존재하거나, 무한히 확장되는 경우에 재귀를 통한 계산이 끝나지 않게 된다.

이러한 문제에 대한 해결책을 아래와 같이 생각해볼 수 있고,
이를 적용하여 Optimal Quantities들을 계산하는 것이 Value Iteration이라고 할 수 있다.

1. States의 반복
   ➡️ 동일한 States에 대한 측정값은 1번만 계산
2. Tree의 무한한 확장
   ➡️ Depth-limited 탐색을 하되 측정값의 변화가 작아질때까지 최대 깊이를 증가시킨 후 탐색
   ➡️ Time-limited values : 상태 $s$에서 $k$번의 step을 더 할 수 있고, 이를 최적값 $V_k(s)$라고 정의
          (= depth-$k$ expectimax)

Value Iteration

바로 위에서의 Time-limited values 방법을 적용한 것이 Value Iteration 이라고 할 수 있다.
다만 여기에서는 따로 $k$ step을 정의하진 않고, Discounting factor $\gamma$를 통해 Time-limited 탐색이 이뤄지도록 암시하고 있다.

1. Value Iteration의 실행 순서

1) Value Update
아래 수식을 통해 $V$를 업데이트 하는 방식이다.

➡️ 시간복잡도 : $O(S^2A)$
       $O(A)$, 1개의 상태에서 선택 가능한 행동의 개수 $A$
       $O(S)$, 1개의 상태에서 특정 행동을 했을 때 이동 가능한 모든 상태 $S'$의 Q-value 계산 $(S=S')$
       $O(S)$, 모든 상태에 대해 위 과정 계산

2) Repeat until convergence
$V(s)$가 수렴할때까지 업데이트를 계속 진행한다.

2. Value Converge

위의 과정을 거치면 과연 $V_k(s)$는 특정값으로 수렴하게 될까?
모든 경우에 해당되지 않고, 아래의 경우 중 하나라도 해당될때만 수렴하게 된다.

1) Finite depth
     : Tree가 무한히 확장하지 않는다면 수렴하게 된다.
2) Discounting factor $\gamma < 1$
     : Tree가 무한히 확장하더라도 얻게되는 $V$ 관점에서는 유한해지기 때문에 수렴하게 된다.

3. 문제점

Value Iteration에는 문제점이 있다. 먼저 MDP의 목적을 다시 떠올려보자.
우리는 $V^*(s)$를 구하는 것이 아니라 특정 상태에서의 최적의 행동 $\pi^*(s)$을 구하는 것이 목적이다.

$V_k(s)$를 구하는 과정을 살펴보면, 특정 상태에서의 행동은 이미 정해졌지만
$V_k(s)$를 수렴시키기 위해 불필요한 계산이 생긴다는 것을 알 수 있다.
     문제점 1) 1개의 반복마다 $O(S^2A)$ 소요
     문제점 2) 각 상태의 "max" 값의 변화 느림
     문제점 3) Policy는 Value보다 먼저 수렴하게 됨

이를 해결하기 위해 Policy 관점에서 계산하는 것이 바로 Policy Iteration 이다.

Policy Iteration

1. Action의 계산 방법

먼저 Policty Iteration에 대해서 알아보기 전에,
어떻게 Value Iteration의 문제점에 대해서 해결할 수 있을지 생각해보자.

Policy(Action)을 구하기 위해서는 Value 또는 Q-Value를 알고 있어야한다.
1) Actions from values
만약 $V^*(s)$를 알고 있다면, Q-Value를 계산하고 이를 maximize 하는 Action을 선택하면 된다.
이러한 과정을 policy extraction이라고 하며, 이미 Value로부터 암시적으로 구해진 policy를 얻는 과정이라고 볼 수 있다.

2) Actions from Q-values
만약 $Q^*(s, a)$를 알고 있다면, 문제는 더 간단해진다.

2. Policy Iteration의 실행 순서

1) Policy Evaluation
모든 Action에 대해 $V(s)$를 계산하는 것이 아닌 $\pi(s)$로부터 주어진 Action에 대한 $V(s)$를 계산한다.

➡️ 시간복잡도 : $O(S^2)$
       $O(1)$, 1개의 상태에서 선택 가능한 행동의 개수 = 1
       $O(S)$, 1개의 상태에서 특정 행동을 했을 때 이동 가능한 모든 상태 $S'$의 Q-value 계산 $(S=S')$
       $O(S)$, 모든 상태에 대해 위 과정 계산

2) Policy Improvement

3) Repeat until convergence
$\pi(s)$가 수렴할때까지 업데이트를 계속 진행한다.
➡️ 시간복잡도 : $O(S^2A)$
       $O(A)$, 1개의 상태에서 선택 가능한 행동의 개수 $A$
       $O(S)$, 1개의 상태에서 특정 행동을 했을 때 이동 가능한 모든 상태 $S'$의 Q-value 계산 $(S=S')$
       $O(S)$, 모든 상태에 대해 위 과정 계산

암시적으로 Action에 대해 계산하는 Value Iteration와는 달리
Policy Iteration에서는 명시적으로 Action에 대해 징저.