이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.
CNN이란?
1. FNN의 한계
기존의 FNN은 고차원의 문제를 해결하기 어렵다. 예를 들어 이미지를 FNN으로 분류한다면 학습 Parameter 개수가 너무 많아진다.
위 그림처럼 1000 x 1000 RGB 이미지가 존재하고, 1개의 Hidden Layer에 100개의 Node를 만든다고 생각해보자.
Input = 1000x1000x3 = 3,000,000 이고 100개의 Node에 매핑되어야 하니 단 1개의 Layer에 총 300,000,000 개의 Parameter가 필요하다.
이걸 Deep Layer로 만든다면.. 자원이 상상 이상으로 많이 필요할 것이다.
2. CNN의 등장
이러한 문제점을 해결하기 위한 아이디어가 바로 Local Processing of Data이다.
이미지를 예로 들자면, 1개 pixel이 의미를 갖기보단 주변 pixel 데이터와의 관련성을 통해 의미를 가지게 된다.
이러한 특징에 기반하여 아래 2가지 가정을 토대로 CNN이 등장하게 되었다.
① Paramter Sharing(특정 부분을 인식하는 필터는 다른 부분을 인식하는데도 유용)
② Sparsity of Connections(출력은 입력의 특정 부분에만 의존)
CNN은 1980년에 Neocognitron이라는 이름으로 등장하였으나 성능이 좋지 않아 주목받지 못했고,
이후 점차 발전하여 CNN 기반의 AlexNet 기존 대비 높은 성능 향상을 보이며 널리 이름을 알리게 되었다.
3. CNN의 구조
Convolutional Neural Networks(CNN or ConvNet)도 마찬가지로 layer를 여러개 쌓은 구조이며,
CNN은 아래 3 종류의 Layer로 구성되어 있다.
- Convolutional Layer : 입력의 Local Region을 활용하여 출력을 계산하는 Layer
- Pooling Layer : Down sampling을 위한 Layer
- Full-Connected Layer : 입력의 전체 데이터를 활용하여 출력을 계산하는 Layer
Convolutional Layer
여기에서는 2D Convolutional Layer에서 다룬다.
일반적으로 우리가 흔히 사용하는 이미지가 입력으로 주어지면 2D Conv. Layer를 사용하고
3D Conv. Layer는 MRI, 3D-Simulation 분야와 같이 X/Y축 뿐만 아니라 Z축에 대한 의미도 중요할때 사용된다.
1. Perceptron의 한계
앞서 말했던 내용을 다시 짚고 넘어가보자.
Perceptron을 사용하면 32x32x3 이미지가 입력으로 주어질 때, 이를 3072x1 형태로 치환한다.
이렇게 되면 ① 2D 이미지의 공간적 의미가 소실되고, ② 너무 많은 Parameter가 필요하다는 문제가 생긴다.
2. Convolutional Layer
기존의 Perceptron이 가지고 있는 문제를 해결하기 위해 Convolutional Layer를 사용하는데,
여기서 Convolve란, 1개의 Filter와 이미지 내에 Filter size와 동일한 Chuck가 여러개 있을 때
모든 Chuck에 대해 Filter와 Dot product 연산을 수행하는 것을 말한다.
아래 그림을 보면 이해가 쉬운데, Convolution 연산은 이미지가 가지는 공간적 의미를 보존할 수 있다.
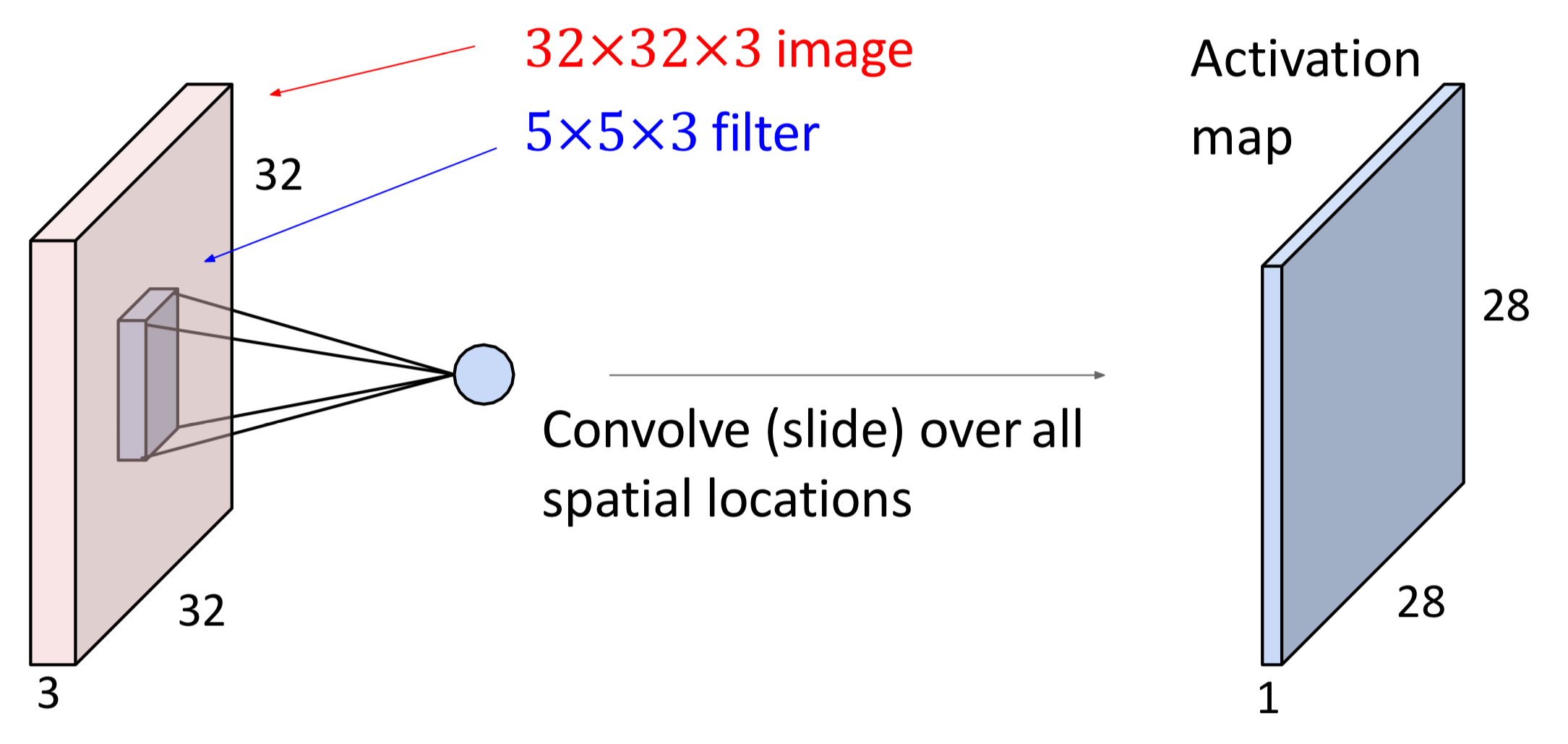
1개의 Filter로 Colvolution 연산을 하면 1개의 Activation Map이 만들어진다.
만약 N개의 Filter가 있다면? N개의 Activation Maps이 만들어지게 된다.
그리고 각각의 Filter는 서로 다른 Parameter를 가지게 된다.
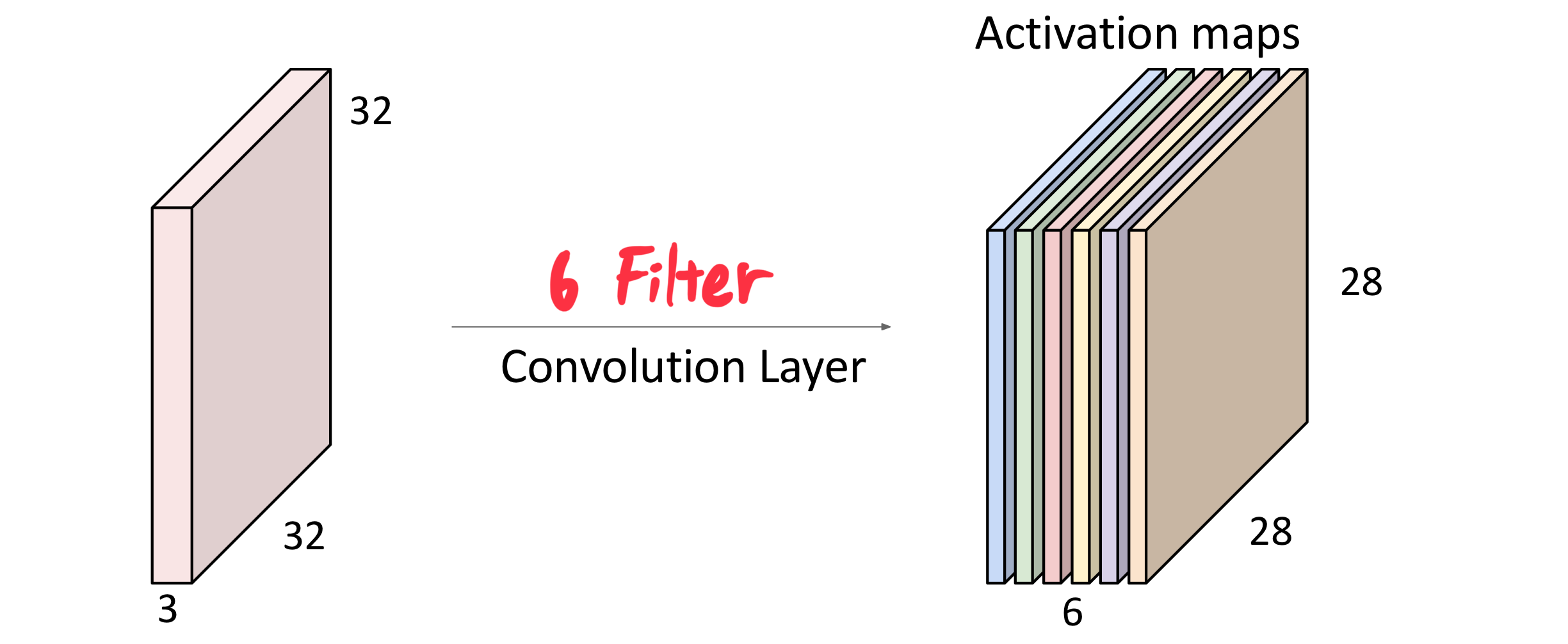
그리고 지금은 2D Convolutional Layer에 대해서 다루고 있기 때문에,
X/Y축에 대해서만 Local Region을 취득하고 있고, Z축(=Channels)은 부분이 아닌 전체에 대해서 계산하고 있다.
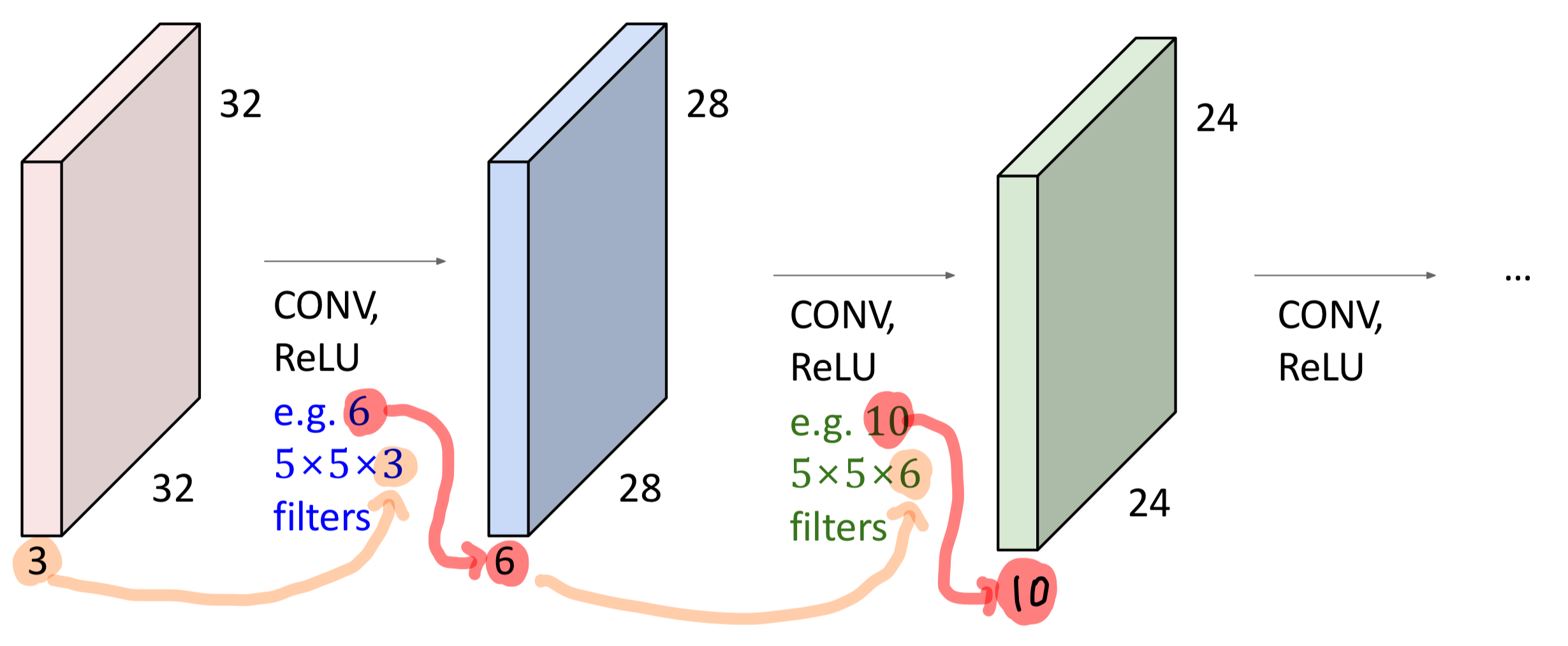
이를 정리하자면 위의 그림과 같이 입력의 Channel 수는 Filter의 Channel 수와 같다.
또한 Filter의 개수는 출력의 Channel 수와 같다는 것을 알 수 있다.
3. Spatial Dimensions
위에서의 Convolution 연산은, 입력의 모든 Chuck에 대해 연산을 수행했다.
그리고 Filter를 통해 여러개의 데이터를 1개의 데이터로 매핑시키기 때문에 입력과 출력의 크기가 달라지게 된다.
이런 부분을 조절하기 위해 Stride, Pad 라는 개념이 존재한다.
1️⃣ Stride
Stride는 모든 Chuck에 대해 연산을 수행하는 것이 아니라, 일부 Chuck에 대해서만 연산을 수행하는 것이다.
이전에는 X/Y축 방향으로 1칸씩 움직이면서 모든 Chunck를 확인하였는데, 만약 2칸씩 움진인다면 어떻게 될까?
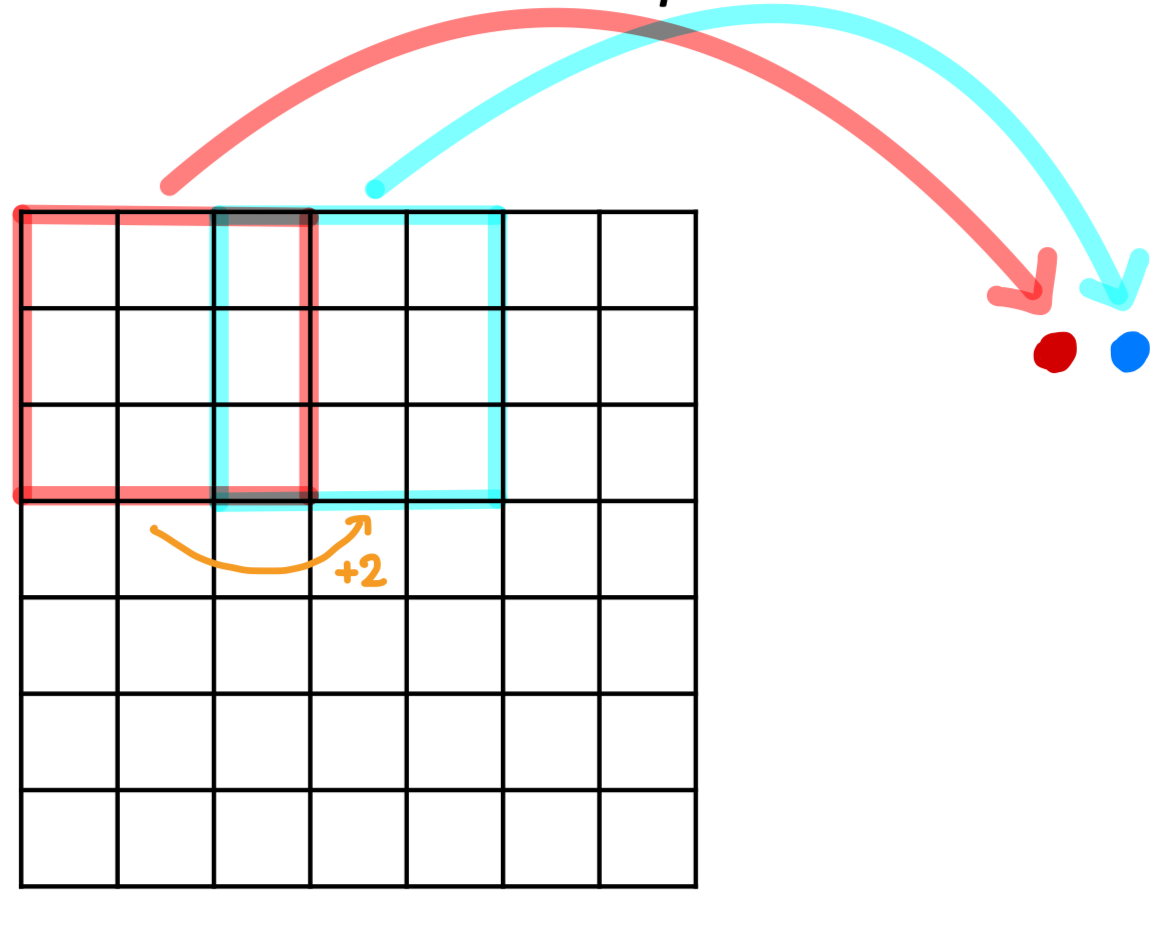
출력의 크기는 더 작아질 것이고, 2칸씩 움직이는 것이 stride=2라고 말할 수 있다.
stride는 컴퓨터의 자원 한계 상 출력의 크기를 감당할 수 없을 때 사용한다.
즉 메모리 및 계산량을 감소시키기 위해 출력 크기를 조절할 때 stride를 사용한다.
2️⃣ Pad
Pad는 Stride와 반대되는 개념이다. 입력 대비 출력의 크기를 줄어드는게 아닌 유지하게 만들어준다.
입력의 가장자리에 임의의 데이터를 입력된 칸만큼 추가하는 것을 의미하며,
Pad=1인 경우 가장자리에 1줄을 추가하게 되고 이는 입력 대비 출력 크기를 유지하게 해준다.
또한 Pad는 가장자리 부분에 연산을 더 적용할 수 있기 때문에, 가장자리(경계) 영역에 대한 정보를 보존시켜준다.
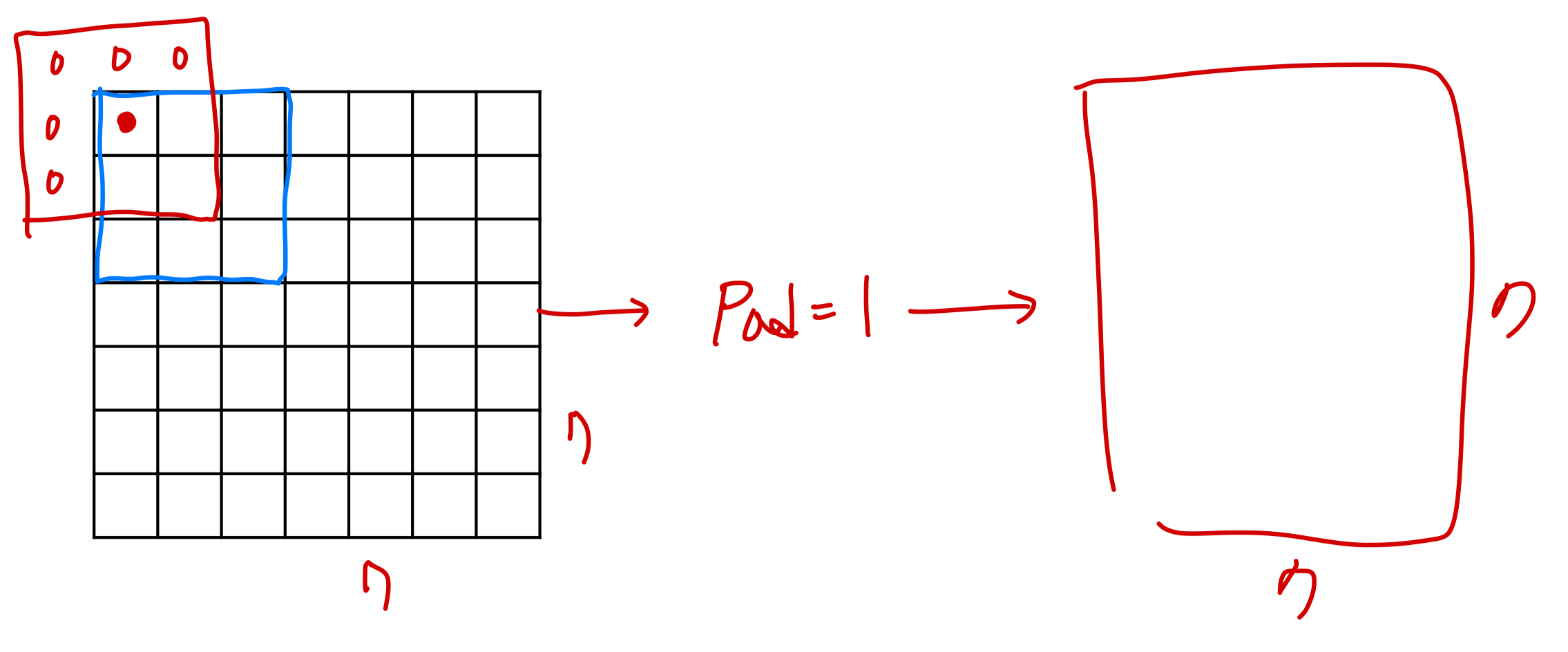
참고로, Pad로 인해 가장자리에 채워지는 데이터는 일반적으로 0을 쓰지만
목적에 따라서 상수 / 또는 학습 파라미터로 적용할 수 있다. (하지만 보통 가장 간단한 0을 쓴다. Simple is Best !...)
Formulation
Stride/Pad를 포함한 Convolution 연산에 대해 입력/출력/Filter Size를 수식화할 수 있다.

4. CNN의 특징
Receptive Fields
Receptive Fields는 Convolution Layer 내의 각각의 Hidden Node의 출력을 구하기 위해서 사용되는 원본 이미지의 부분 크기를 의미한다.
초기 Layer에서는 1개의 Hidden Node를 구하기 위해 사용되는 크기가 보다 작겠지만, Layer가 깊어질수록 크기가 더 커지게 된다.
이는 Layer가 더 깊어질수록 더 넓은 영역을 고려하게 된다는 것을 의미한다.
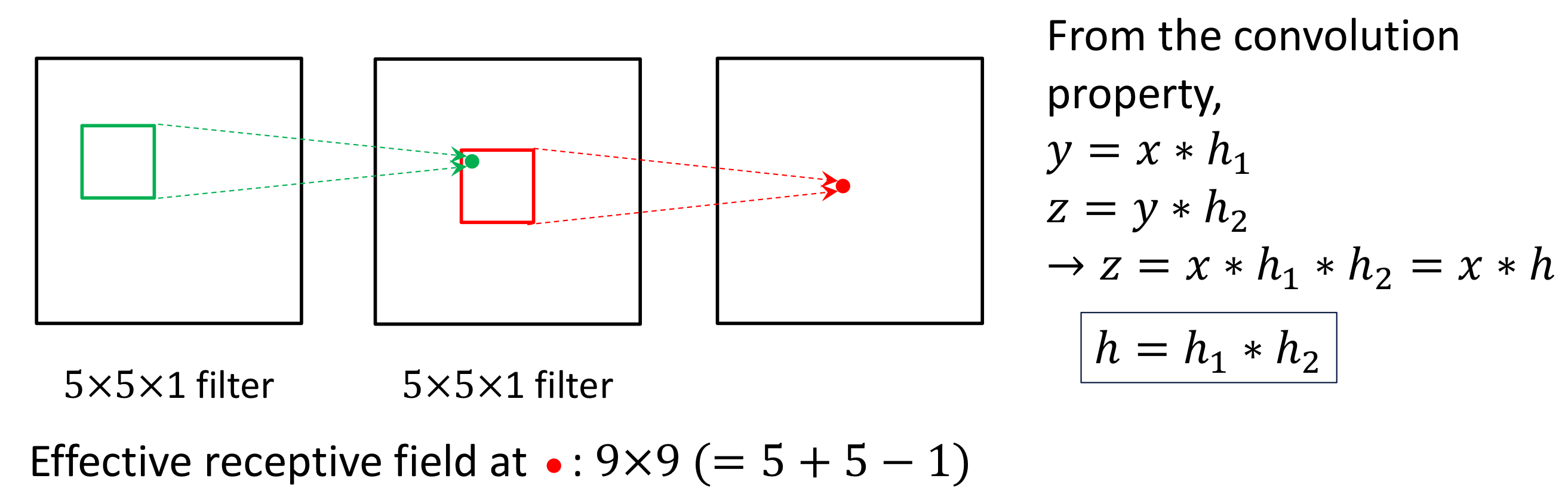
<계산과정 추가>
Hierarchy of Convolutional Layers
입력이 오른쪽의 자동차 이미지가 주어졌을 때 Filter와 Filter의 출력을 살펴보면 계층적으로 이미지에 대한 의미를 파악하는 것을 알 수 있다.
이는 사람의 인지 과정과 유사하게 정보를 이해하고 분석하는 것을 의미하며 이러한 과정을 Semantic Hierarchy라고 설명한다.
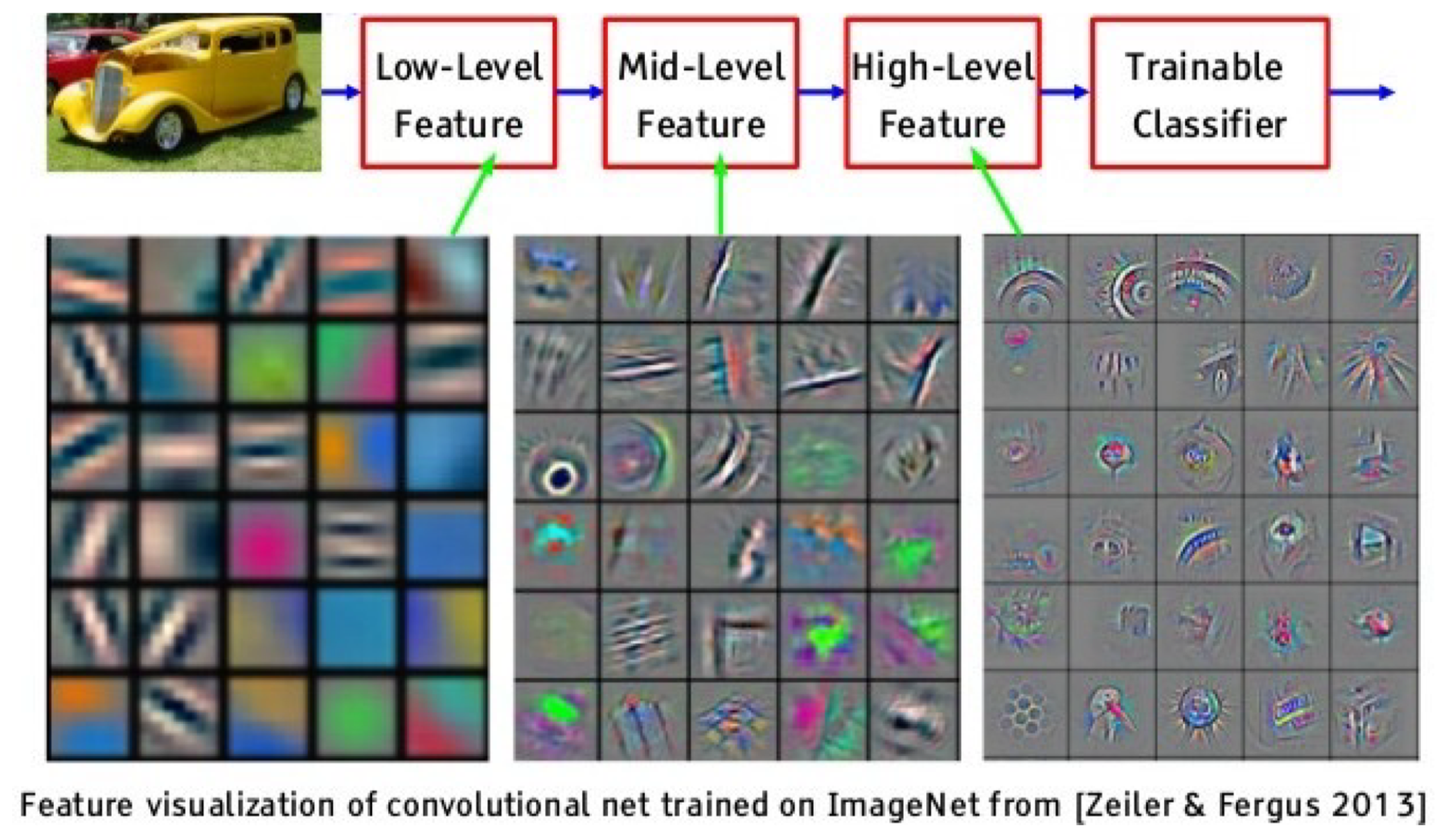
Low-Level(=Filter)에서는 Edge, Color 등 이미지로부터 얻어낼 수 있는 기본적인 패턴을 추출해오고
Mid-Level(=Filter의 출력)에서는 부분적인 구조를, High-Level(=Filter의 출력)에서는 더 복잡한 구조나 의미적인 정보를
추출해 오는 것을 볼 수 있다.
5. Backpropagtion
Pooling Layer
Pooling Layer는 이미지의 특징을 유지하면서 크기를 줄이는 목적을 가진다.
다만 Channel의 수는 그대로 유지된다.
1. Spatial Dimension
Pooling은 Channel에 대해서 독립적으로 수행되기 때문에 입력의 채널 수는 출력의 채널 수와 같다.
이 외에는 Convolutional Layer와 동일하다.
2. Backpropagation
Max Pooling을 했다면, Max 값을 취한 위치를 기억해두고 Backprogation 과정에서
Upstream Gradient를 해당 위치에 그대로 곱해주고, 아니라면 0을 곱해준다.
Average Pooling의 경우, M개의 원소가 있다면 각각의 Local Gradient에
Upstream Gradient의 1/M을 곱해주면 된다.