기계학습 #2 Logistic Regression

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

---

Classification(분류)

이전 글에서 Regression(회귀)에 대해서 다뤘고,
부동산 가격이나 키와 같은 연속적인 값을 추정하는 것을 Regression이라고 했다.

그렇다면 이런 연속적인 값이 아닌 이산적인 값을 추정한다고 해보자.
이메일이 스팸인지 아닌지 또는 종양이 양성인지 악성인지와 같이 이산적인 값을 추정하는 것을
우리는 Classification(분류)라고 한다.

이번 글에서는 Classification과 이를 위한 알고리즘인 Logistic Regression에 대해서 설명하고자 한다.

1. 정의

위에서 말한 내용을 정리하자면 Classification은 아래와 같이 정의할 수 있다.

• 독립 변수 $\text{x}$ 는 Regression과 동일하다.
• 종속 변수 $\text{y}$ 는 Regression과 달리 이산적인 값(Categorical)을 가진다. $(\text{y} \in \{0,1\})$

2. Classification with Linear Regression

먼저 Classficication(분류) 문제의 Mapping function으로 Linear Regression을 사용해보자.

파란색 1번이 Linear Regression을 사용했을때 나올 수 있는 최선의 함수일 것이다.
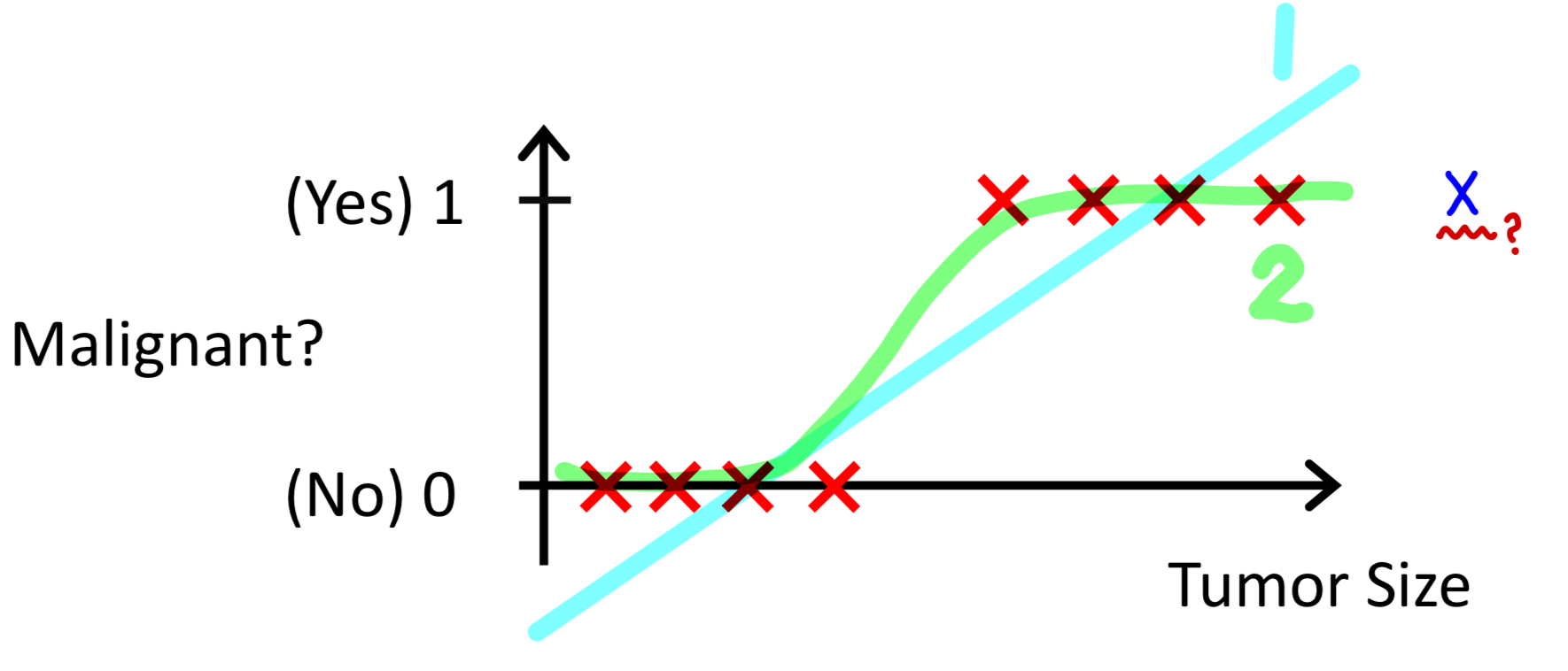
Classification 문제에서는 Mapping function의 결과값이 0 또는 1로 반환되어야 하는데,
Linear Regression을 사용하게 되면 그림과 같이 Tumor Size(X인자)가 커지면 커질수록
Mapping function의 값은 1보다 큰 값을 반환한다는 것이다.

이를 해결하기 위해서는 초록색 2번과 같이 Mapping function의 결과값을 0과 1 사이로
Normalize(정규화) 하고 Threshold 0.5를 기준으로 0.5보다 크거나 같으면 1, 작으면 0을 반환하는 방법이 있다.

이렇게 기존의 Linear Regression의 결과값을 정규화하는 Mapping function
Logistic Regression이고, 아래 내용에서 더 자세히 다뤄보고자 한다.

Logistic Regression

이름에 Regression이 들어가서 Regression 문제에서 사용되는 알고리즘으로 오해할 수 있으나,
이는 Classification 문제에 사용되는 알고리즘이라는 점을 확실히 해두자 !

1. Mapping function

1) Mapping function 설계

위에서 말했던 것과 같이, Linear Regression 값을 0과 1 사이의 값으로 정규화하는 Mapping function을 사용한다.
이를 위해 여기에선 sigmoid function을 사용한다.

sigmoid function은 주어진 $z$를 아래 수식을 통해 0과 1 사이의 값으로 정규화하는 함수이다.

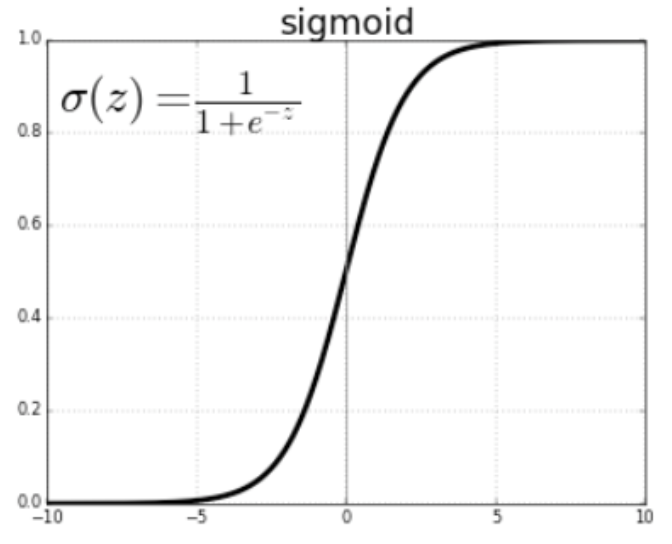
Logistic Regression에서는,
sigmoid function에 회귀식을 입력하여 반환되는 출력값을 사용한다.
이를 수식으로 다시 나타내면 아래와 같다.

2) Mapping function 해석

이렇게 Mapping function $f_w(x)$을 구성하게 되면 출력값은 0과 1 사이의 값으로 반환된다.
Linear Regression에서 $f_w(x)$의 값은 y에 대한 추정값이었는데,
Logistic Regression에서 $f_w(x)$의 값은 y = 1 인 확률로 해석할 수 있다.
예를 들어 $f_w(x)=0.7$ 인 경우, y=1일 확률이 70%, y=0일 확률이 30%라고 말할 수 있다.

3) Decision Boundaray (결정 경계)

위에서 sigmoid function에 대한 이미지를 보면, $z=0$일 때, 반환값(=확률)이 0.5임을 알 수 있다.

여기서 $z=-w^{\text{T}}x$, 우리가 구하게 될 회귀식이기 때문에 아래와 같은 특징을 알 수 있다.

이러한 $x$에 관한 회귀식 $w^Tx$를 좌표계에 나타내게 되면
우리가 구하고자 하는 $y$ 를 분류해주는 경계가 그려지고 이를 Decision Boundary(결정 경계)라고 한다.

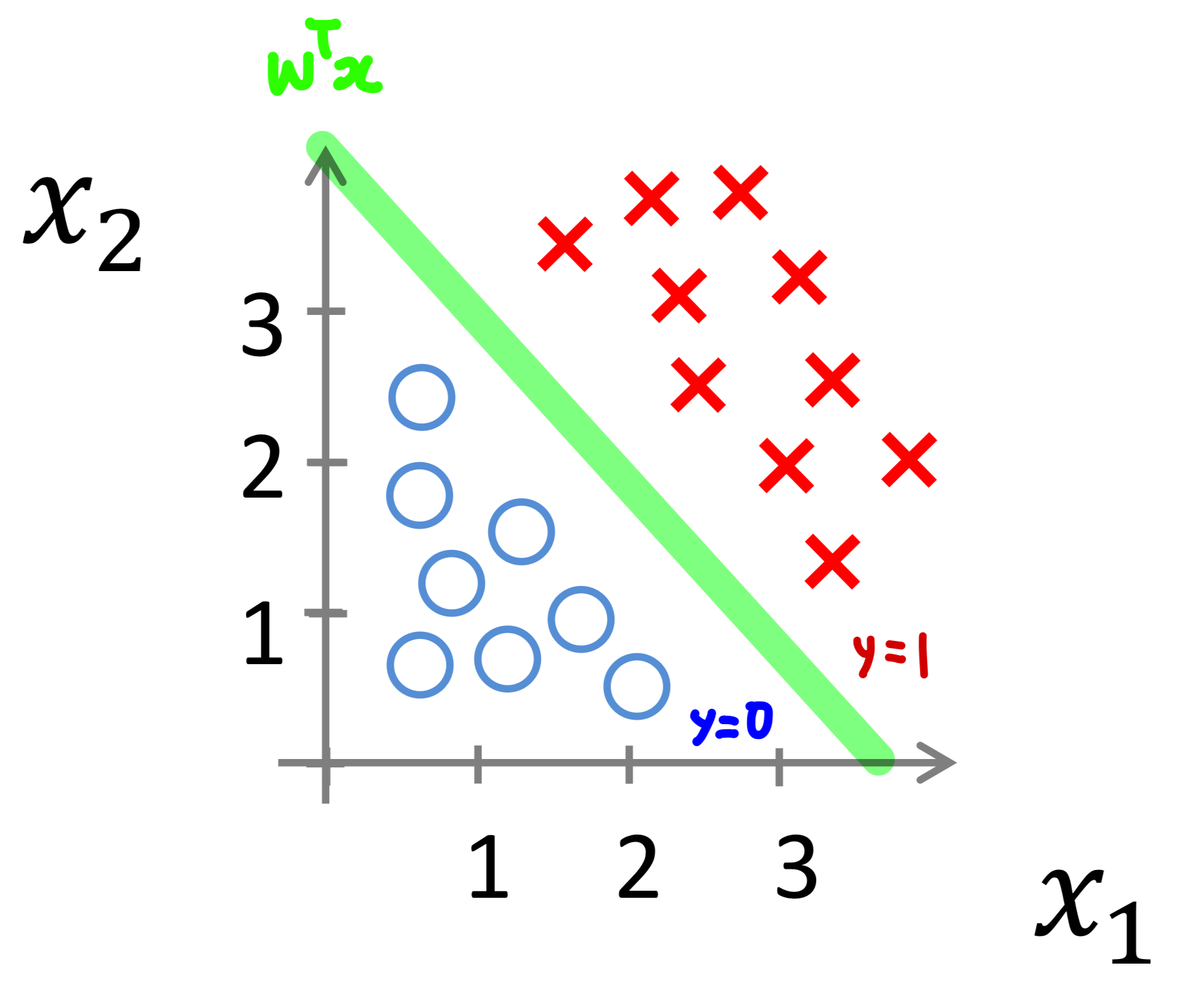
위에서 그려진 Decision Boundary는 선형이다.
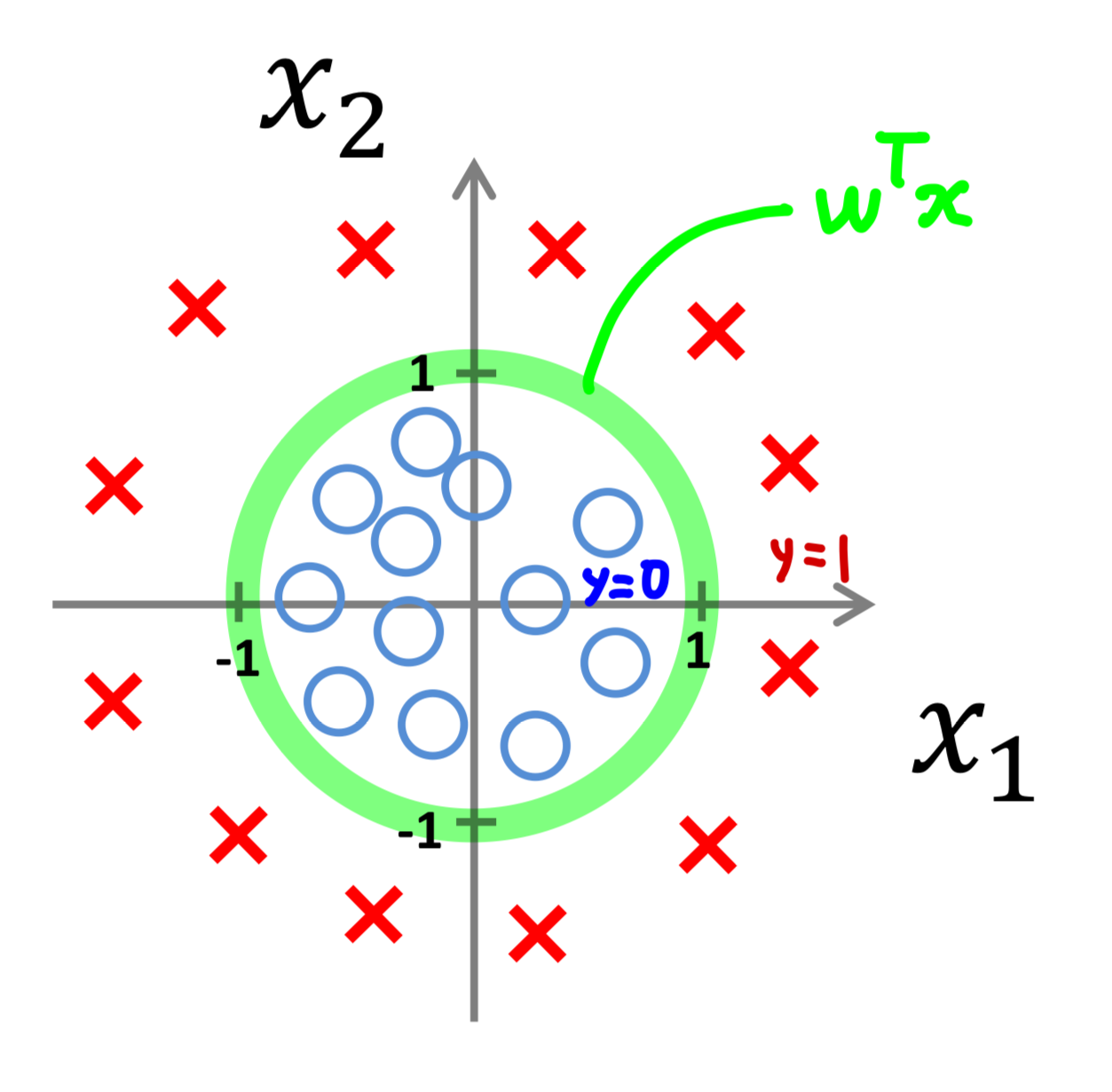
그렇다면 비선형(Non-linear) Decision Boundary는 어떻게 구할 수 있을까?

간단하다. $w^{\text{T}}x$ 에 비선형 인자를 추가하면 된다.
$f_w(x) = g(w_0 +w_1x_1+w_2x_2)$에는 선형 인자로만 이루어졌기 때문에 선형의 경계가 나타난다.

여기에 $x^2$ 형태의 비선형 인자를 추가한다면, 아래와 같이 비선형의 경계를 구할 수 있다.
$f_w(x) = g(w_0 +w_1x_1+w_2x_2+w_3x_1^2+w_4x_2^2)$

※ sigmoid function에 대해서 좀 더 깊게 알고 싶다면, 아래 Link를 참조하면 좋을 것 같다.

• sigmoid function의 유래
• Logistic Regression에서 sigmoid 출력값과 확률의 관계

우리는 위에서 분류 문제에 대한 Mapping Function을 설계했다.
분류 문제도 결국 회귀 문제와 동일하게 최적의 파라미터 $w$* 를 찾는 것이기 때문에,
이를 찾기 위해선 분류 문제에 맞게끔 Cost function과 Optimization에 대해서 설계해야한다.

2. Cost function

여기에서도 이전처럼 회귀 문제에서 사용했던 Cost function 인 MSE를 분류 문제에 적용해보자.

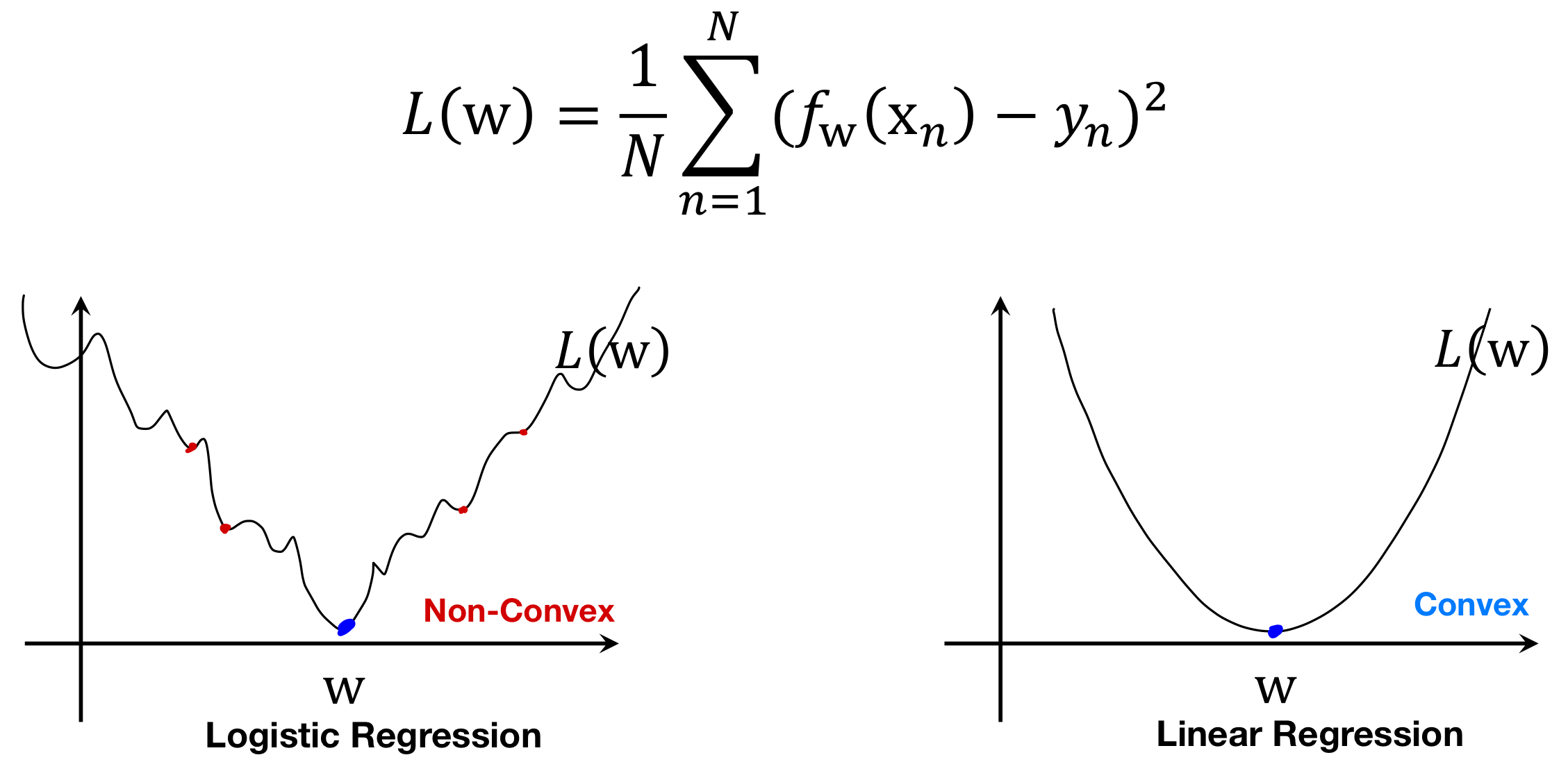
그럼 아래와 같이, Cost Curve가 Non-Convex 한 형태로 나타나게 됨을 알 수 있다.
Non-Covex Cost Curve 는 Local minima가 많이 존재하기 때문에 경사하강법에서는 Global minima에 도달하기 어렵다는 단점이 있다.

그렇기 때문에 우리는 Conve Cost Curve를 가질 수 있도록 분류 문제에 알맞는 Cost function을 설계해야한다.

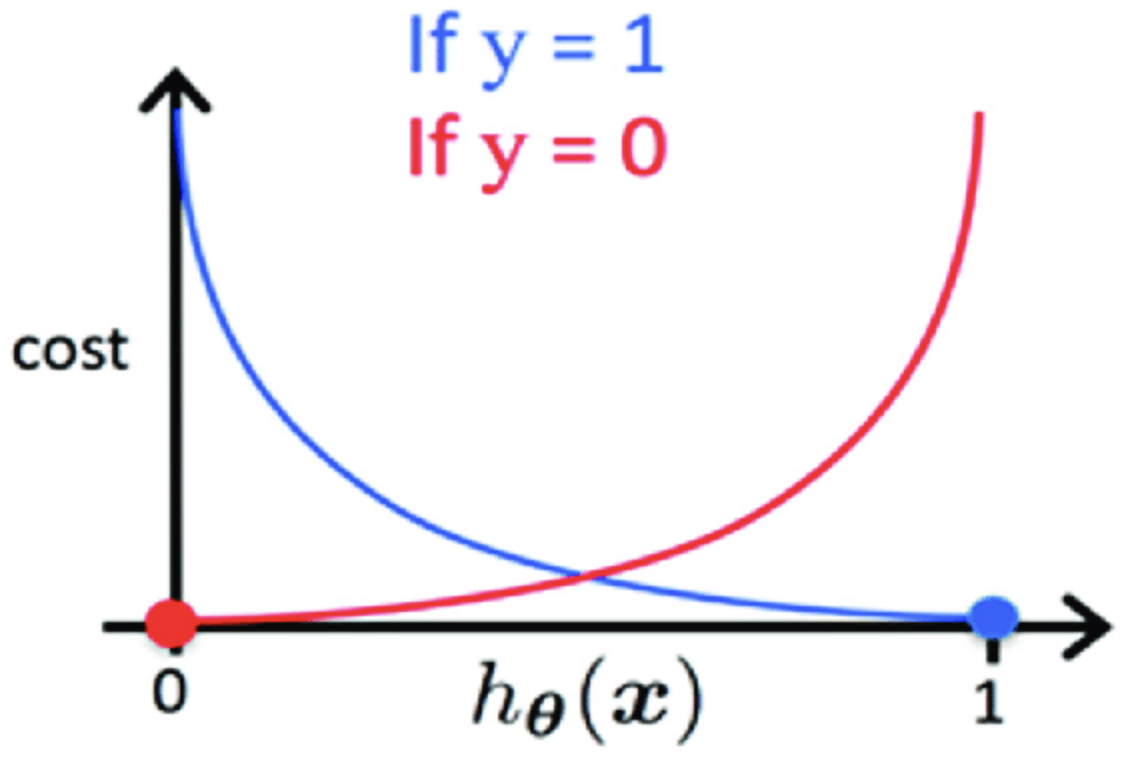
$y_n=0,\;f_w(x_n)=0$ 이면 실제값을 정확하게 추정하였으니 $\text{Cost}=0$이겠지만,
$y_n=0,\;f_w(x_n)=1$ 이면 실제값과 다르게 추정하였으니 $\text{Cost}\rightarrow\infty$와 같이 큰 값을 반환해야 한다.

① 틀린 값에 대해선 매우 큰 Cost를 부여하고, ② Convex Cost Curve를 만족하게끔
Cost function을 설계하면 아래의 수식과 같고, Cost Curve는 그림과 같이 나타난다.

위의 Cost function 수식을 한 줄로 나타내면 아래와 같다.
$y_n=1$일때는 1번째 항만 남아있고, $y_n=0$일때는 2번째 항만 남게 되어 위에서의 수식과 같아진다.

3. Optimization

여기에서도 이전처럼 회귀 문제에서 사용했던 Gradient Descent를 분류 문제에 적용해보자.

Gradient Descent는 오차 $L(w)$를 $w$에 대해 편미분함으로써 기울기를 구하고
구해진 값에 따라 $w$를 업데이트함으로써 최적의 $w$* 를 찾는 방법이다.

그렇다면 Logistic Regression의 $L(w)$를 $w$에 대해 편미분 해보자.
놀랍게도 Linear Regression에서 MSE를 편미분했을때와 굉장히 유사한 식이 나온다.

Logistic Regression에서 Cost function의 수식이 굉장히 복잡해졌지만,
경사하강법에서의 계산을 염두에 두고 설계되었기 때문에 편미분 결과가 위와 같이 나오는 것이다.
그렇기 때문에 우리는 기존의 경사하강법을 그대로 차용하여 사용하면 최적의 $w$* 를 찾을 수 있을 것이다.

Multi-Class Classification

위에서는 지금까지 Binary-Class에 대한 Classification을 진행해왔지만,
실제로는 Multi-Class에 대한 Classification도 요구 된다.

Multi-Class 분류를 위한 방법에는 대표적으로
OvR(One vs Rest), OvO(One ve One) 2가지가 존재한다.

1. OvR (One vs Rest)

가장 직관적인 방법으로, 다중 분류 문제를 이진 분류 관점에서의 문제 여러개로 나누어 해결하는 방법이다.

아래 그림과 같이 3개의 Class가 있다면,
Class 1 ↔︎ Class 2/3 , Class 2 ↔︎ Class 1/3 , Class 3 ↔︎ Class 1/2
3개의 데이터 세트와 분류기를 만들고, Mapping function 값이 가장 큰 Class를 찾아내는 방식이다.

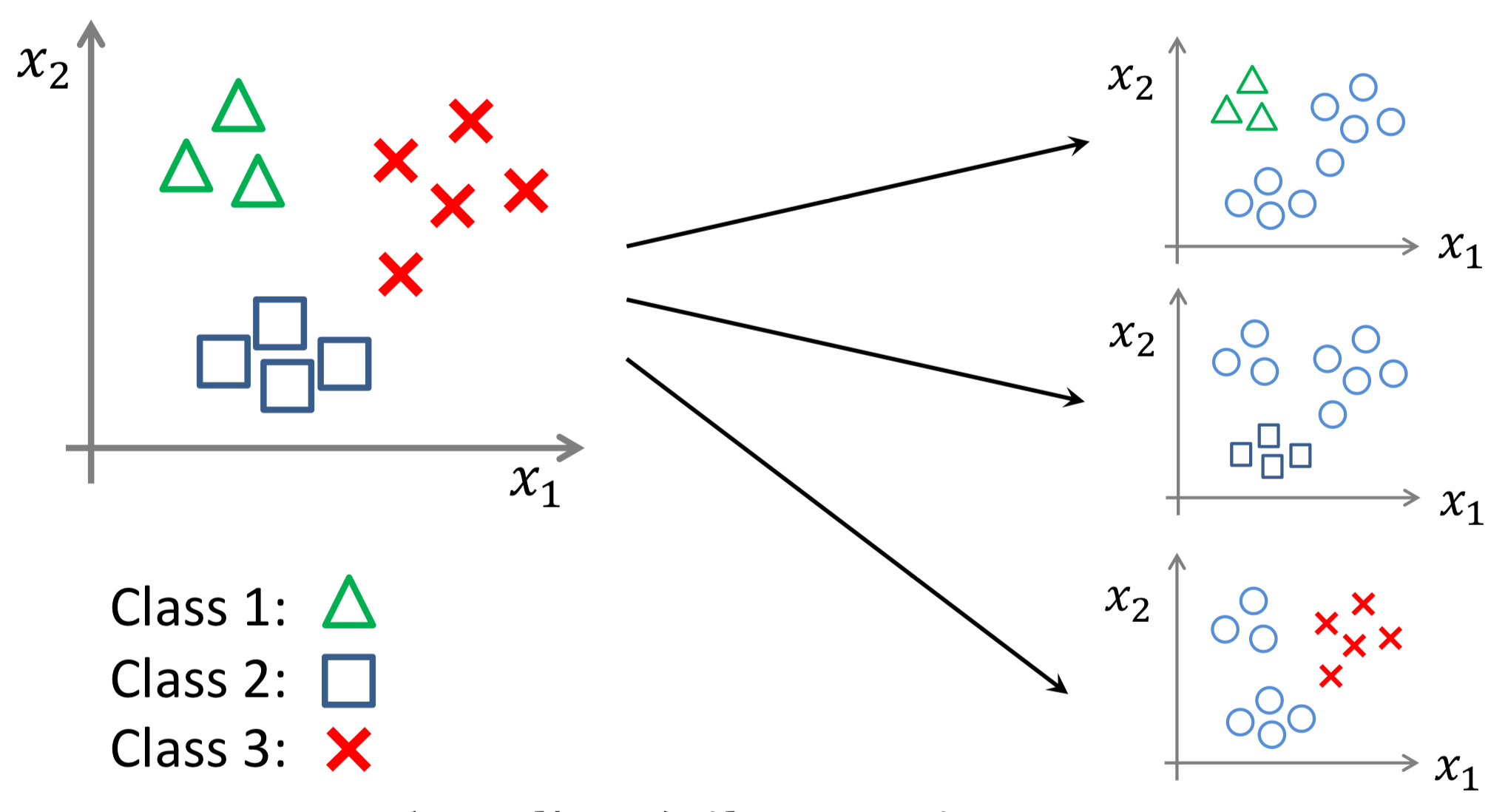
이러한 방식에서 Classifier 는 Class 개수만큼 만들어진다.

2. OvO (One vs One)

또 다른 방식인 OvO도 이진 분류 관점에서의 문제로 전환하는 건 같지만,
OvR는 1개 Class vs 나머지 Class 형태로 비교했다면
OvO는 1개 Class vs 1개 Class 형태로 비교하는 방식이다.

3개의 Class가 있다면 OvO 방식에서는 아래와 같이 1대1 비교를 하도록 구성한다.
Class 1 ↔︎ Class 2 , Class 2 ↔︎ Class 3 , Class 3 ↔︎ Class 1
그리고 각 분류기로부터 예측 된 Class 중에 가장 많이 예측 된 Class를 최종 예측값으로 사용한다.

이러한 방식에서 Classifier는 Class의 개수가 n이라면 $_nC_2$개 만큼 만들어진다.