기계학습 #3 Overfitting / Regularization

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

---

머신러닝의 Framework에 대해서 한번 생각해보자.
우리는 지금까지 1️⃣ 주어진 데이터에 대해 Mapping function을 구하는 과정을 거쳐왔다.
이렇게 구해진 Function을 가지고 2️⃣ 새로운 데이터에 대해서 $y$를 예측하는 과정을 거칠 것이다.
이 과정을 각각 1️⃣Training, 2️⃣Testing 이라고 말할 수 있다.

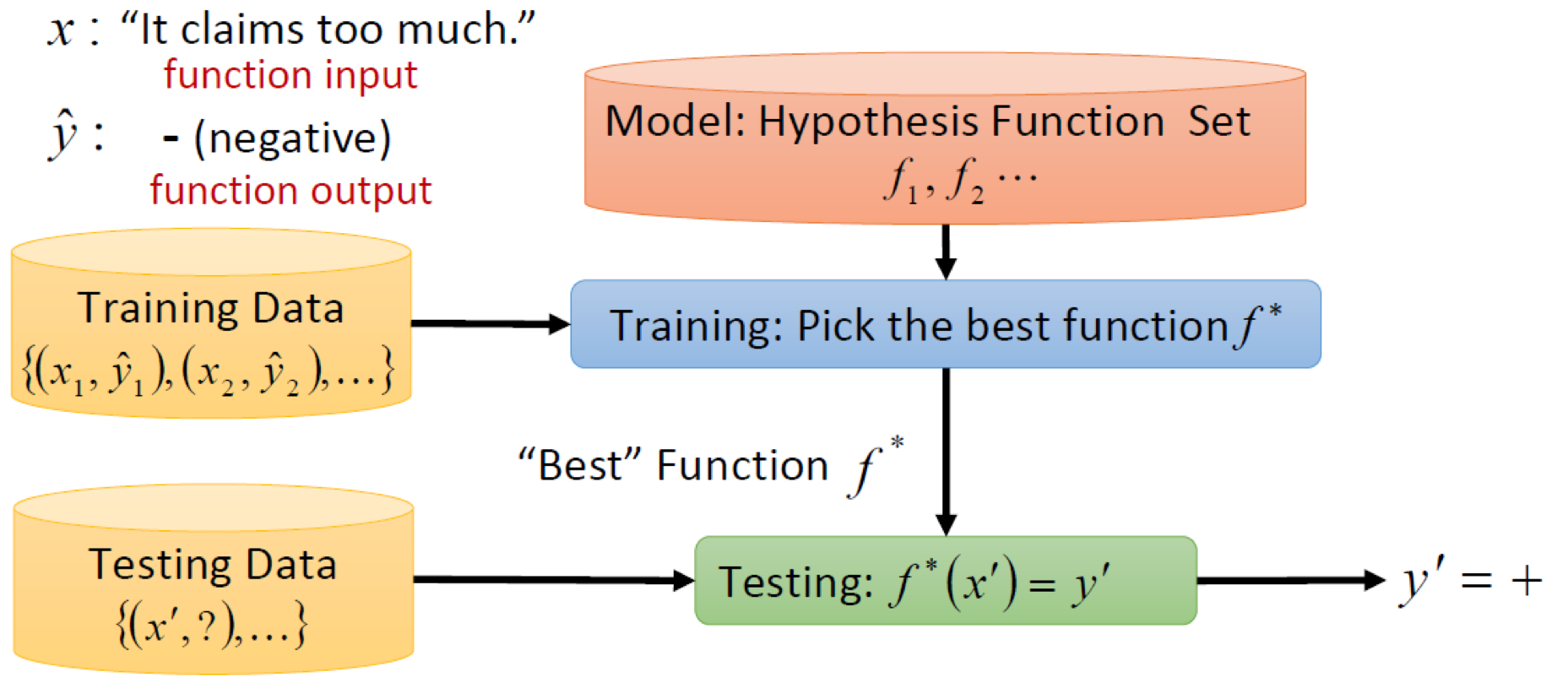
지금까지 Training에 대해서만 다뤄왔지만, 실제로는 구해진 Function을 통해 Testing하는 과정이 중요하다고 말할 수 있다. 우리는 결국 새로운 데이터에 대해서 잘 예측할 수 있는 Function을 구하기 위해 Training 과정을 거치는 것이기 때문이다.

그럼 아래에서 Trainig / Testing 과정 중에 생기는 문제들에 대해서 살펴보고,
어떤 식으로 문제들을 해결할 수 있는지 알아보자.

Underfitting / Overfitting

만들어진 Model(=Function)은 너무 간단하거나 또는 너무 복잡할 수 있다.
여기에 대해서 우리는 아래와 같이 정의 할 수 있다.

1. 정의

• Underfitting (과소적합) : 주어진 데이터를 잘 설명하지 못하는 경우
• Overfitting (과대적합, 과적합) : 복잡도가 높아 주어진 데이터가 가지고 있는 Noise까지 설명하는 경우

Underfitting, Overfitting 모두 만들어지는 Model이 피해야 할 특징이다.

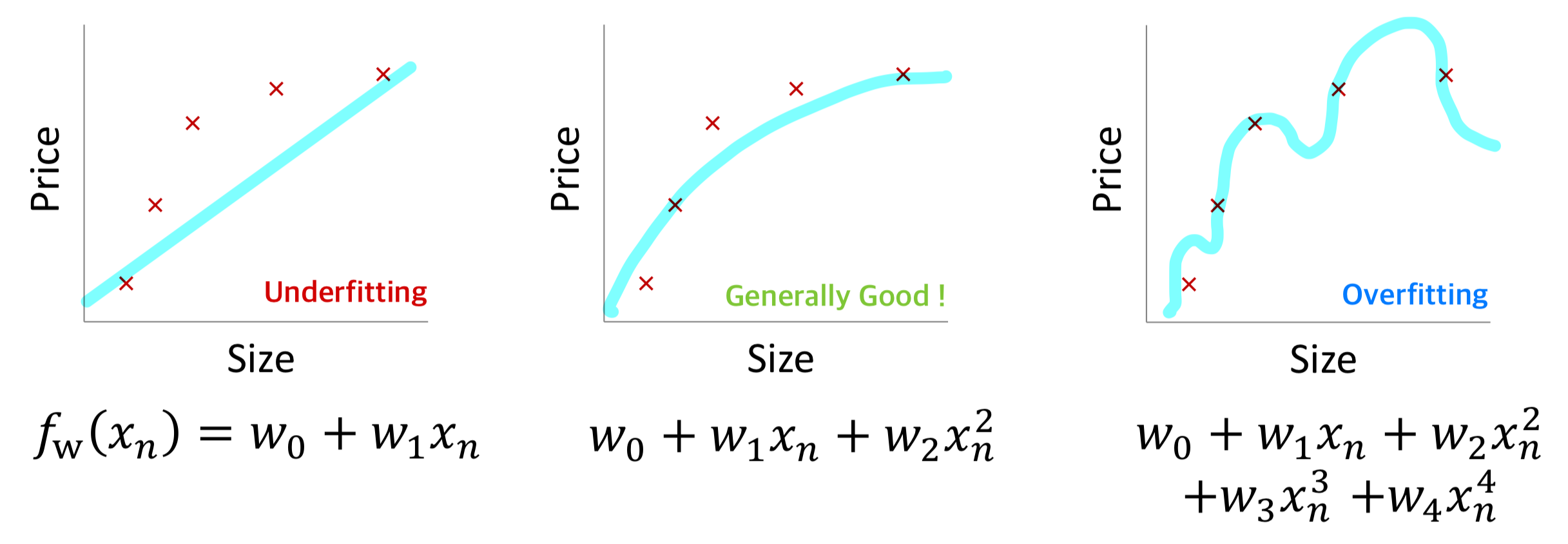
먼저 회귀 문제에서의 Underfitting, Overfitting의 경우에 대해서 살펴보자.
왼쪽이 Underfitting이고 Model이 단순하여 주어진 데이터에 대해 제대로 예측하지 못하고 있다.
오른쪽은 Overfitting이고 Model의 복잡도가 높아 데이터가 가지고 있는 Noise까지 예측하여 예측값과 실제값의 차이가 없음을 알 수 있다.
가운데는 예측값과 실제값의 차이는 발생하지만 데이터가 가지고 있는 경향을 추정하고 있는 것을 알 수 있다.

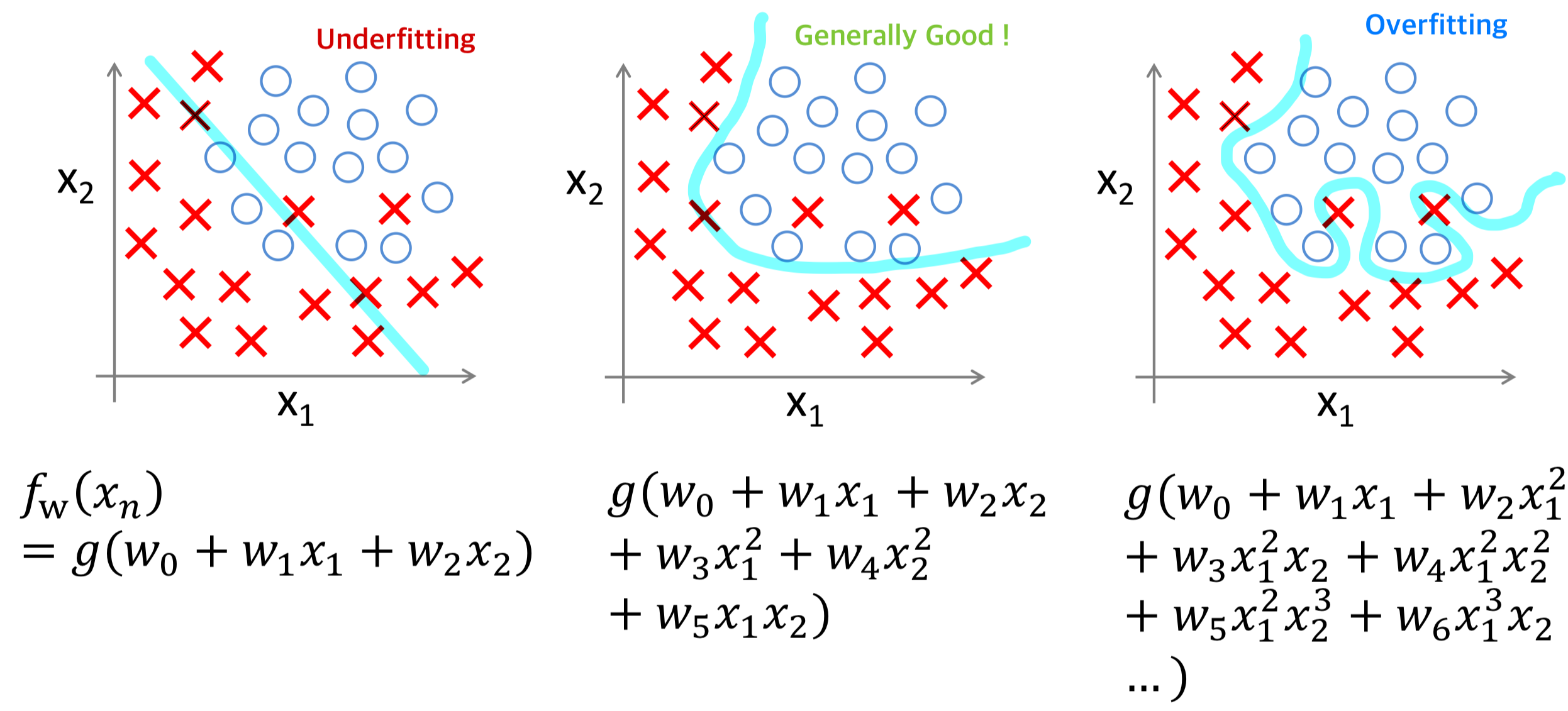
또한 분류 문제에서의 Underfitting, Overfitting은 아래와 같이 나타낼 수 있다.

2. Overfitting은 왜 불필요할까?

Underfitting은 우리가 만들고자 하는, 데이터를 잘 설명하는 Model이 아니기 때문에 불필요하다는 걸 알 수 있다.
그렇다면 Overfitting는, 데이터를 완벽하게 설명하여 Error가 전혀 발생하지 않는데 불필요한 성질인걸까?
그 부분은 Testing에 대해서 고려해보면 알 수 있다.

우리는 궁극적으로 주어진 데이터를 잘 설명할 수 있는 Model 보다는,
주어진 데이터를 통해 새로운 데이터를 잘 설명할 수 있는 Model을 만든는 것이 목적이다.

그리고 일반적으로 데이터는 Noise를 가지고 있기 때문에,
주어진 데이터가 가지고 있는 Noise 까직 완벽하게 학습하기 보단 데이터가 가지고 있는 경향을 학습하는 것이 필요하다.

그래야지만 Model이 새로운 데이터에 대해서도 잘 예측해낼 수 있기 때문이다.

3. Overfitting에 대한 해결책

그렇다면 우리는 어떻게 Overfitting을 막을 수 있을까?
Overfitting을 막기 위해선 아래와 같은 방법들이 있다.

1️⃣ More training data
학습을 위한 데이터를 추가하는 방법으로 Overfitting을 막을 수 있다.
Overfitting은 Model이 데이터가 가지고 있는 Noise까지 학습함으로써 생기는 특징이다.
그러므로 많은 데이터를 통해서 Model이 특정 데이터가 가지고 있는 Noise까지 학습하지 않도록 하는 방법이다.

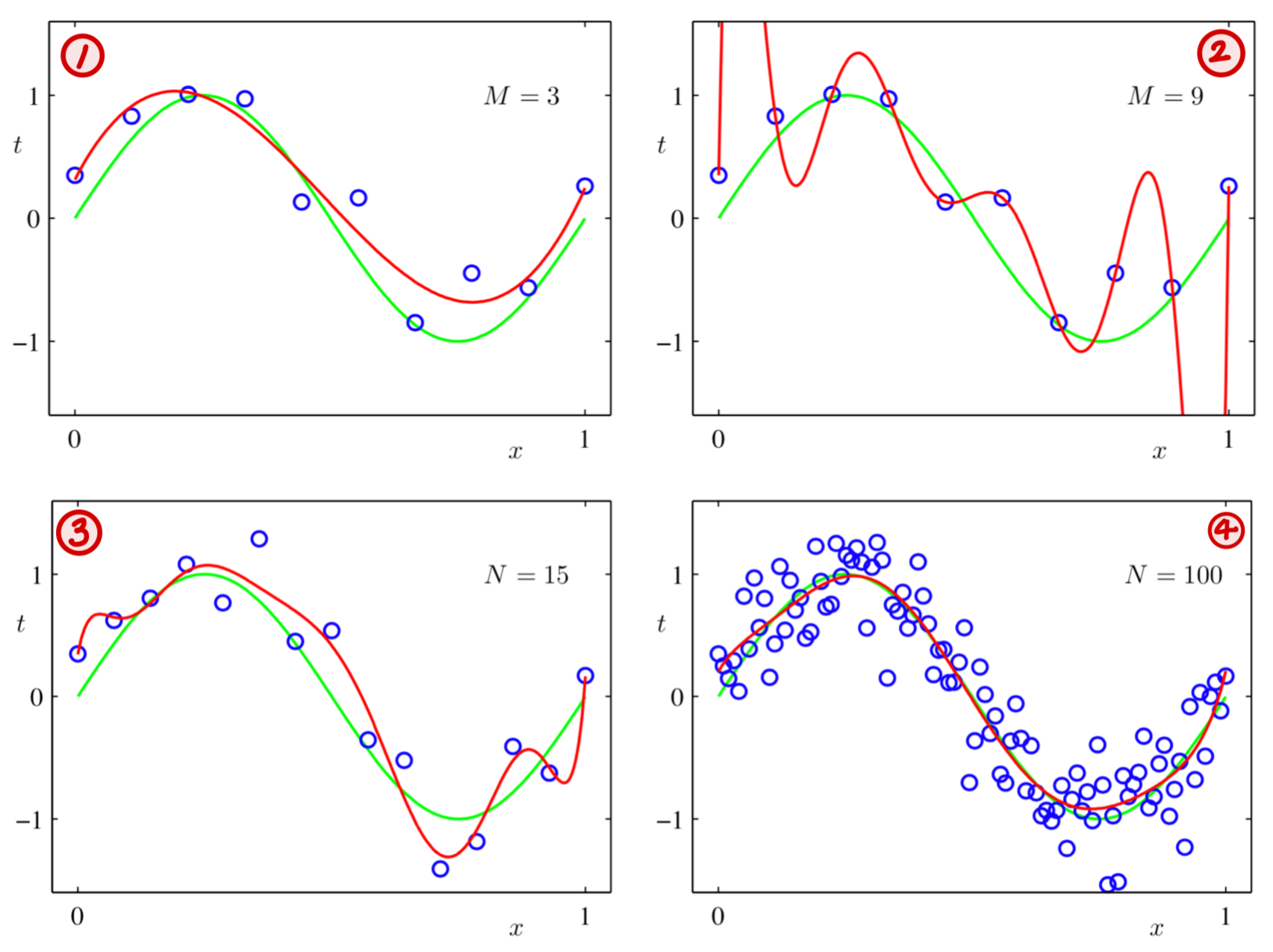
위의 그림에서 초록색 선은 Ground truth(실제 정보), 빨간색 선은 Learned modeld이다.
그리고 N은 학습 데이터의 개수, M은 Model이 가지고 있는 X인자의 차수이다.

1번째 그림에서는 Model이 데이터를 잘 설명하고 있으나, $M=9$ 로 변경하여 Model의 복잡도를 증가시키면 주어진 데이터의 Noise까지 설명하게 되는 Overfitting이 발생하게 된다.

3번째 그림에서 학습 데이터의 개수를 증가시키면 Overfitting이 완화되고,
4번째 그림에서 학습 데이터의 개수를 더욱 더 증가시키면 Model ↔︎ Ground truth 간의 차이가 거의 없음을 확인 할 수 있다.

2️⃣ Simple Model
다른 방법으로는 Model이 가지고 있는 복잡도를 완전히 제거하는 방법이다.
예를 들어, Model X인자가 가지고 있는 차수를 낮춤으로써 복잡도를 완전히 제거할 수 있다.
하지만 데이터가 가지고 있는 복잡성이 어느 정도인지 모르기 때문에 오히려 Underfitting이 발생할 수 있다는 Risk가 존재한다.

3️⃣ Regularization
위에서 설명했듯이 Model의 복잡도를 완전히 낮춘다면 Underfitting이 발생할 수 있기 때문에,
이를 위한 해결책으로 Model이 가지고 있는 복잡도는 유지하되, 영향력을 줄이는 방법이 있다.

우리는 Cost function의 값이 줄어드는 방향으로 $w$를 업데이트 시킨다.
그렇다면, 아래와 같이 Cost function의 값에 $w$ 값을 더해주면 어떻게 될까?

$w_1$ 값이 Cost function에 미치는 영향이 크기 때문에, $w_1$ 값이 0에 가깝게 줄어들 것이다.
이를 통해서 우리는 Model이 가지는 복잡도는 유지하되 영향력은 줄어들게끔 할 수 있다.
이러한 방법을 Regularization이라 하고, 아래에서 더 자세히 설명하고자 한다.

Regularization

1) Regularization 정의

Regularization은 $w$ 값을 Cost function에 반영하여 $w$ 값이 필요 이상으로 커지는 것을 억제함으로써
Model의 복잡도가 적정한 수준을 가지도록하여 Overfitting을 방지하는 기법이다.

이를 수식으로 나타내면 아래와 같다.
기존의 $L(w)$ 뒤에 $\lambda\sum$ 항이 추가되었는데, 이 부분을 regularizer라고 하고
$\lambda$라는 hyper parameter를 통해 regularization의 강도를 조절할 수 있다.

위 수식은 아래와 같이 표현할 수 있으며, $\Omega(w)$ 항을 regularizer 라고 한다.

2) Regularization 종류

1️⃣ L-2 Regularization
대부분의 경우에 Euclidean norm(L-2 norm)을 사용하여 regularizer를 설계한다.

$L(w) = \text{MSE}$ 이고 L-2 Regularization을 사용하는 경우 Ridge Regression 라고 한다.

2️⃣ L-1 Regularization

$L(w) = \text{MSE}$ 이고 L-1 Regularization을 사용하는 경우 Lasso Regression 라고 한다.
L-1 Regularization은 L-2 대비 parameter를 sparse 하게 만든다는 특징이 있다.

3) L1 vs L2

L1과 L2의 Cost Curve

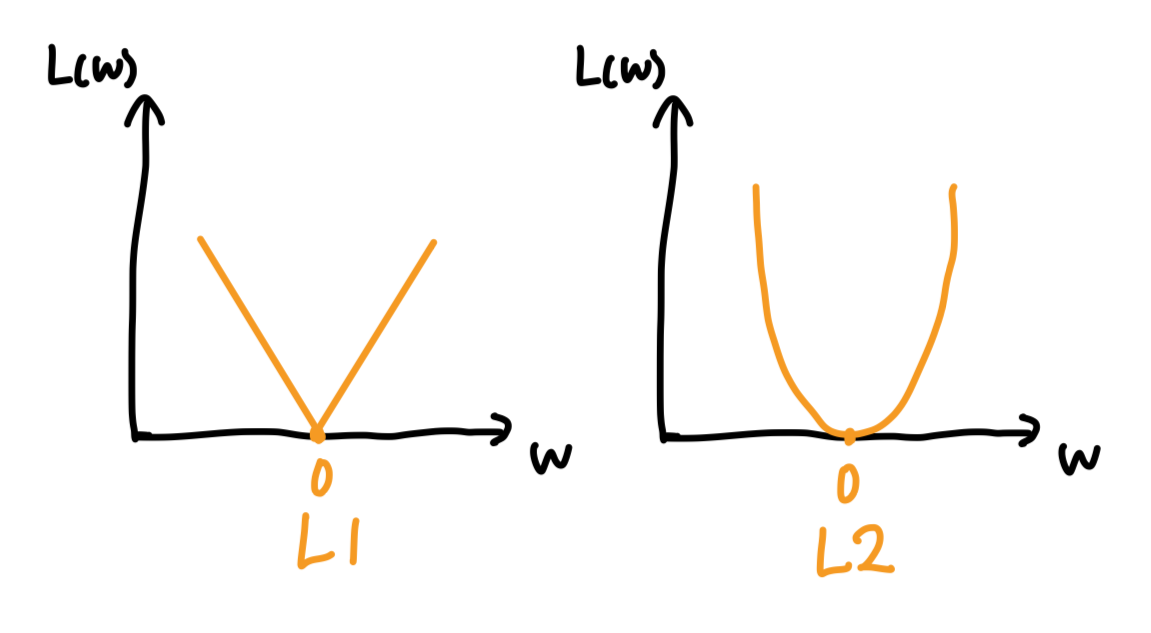
L1은 절대값을 사용하기 때문에 0을 제외한 구간에서 기울기의 크기(부호 제외)가 동일한 것을 알 수 있다.
L2는 제곱을 사용하기 때문에 0과 가까워질수록 기울기의 크기가 작아지는 것을 알 수 있다.

경사하강법에서는 미분(기울기값)을 통해 $w$를 업데이트하게 되는데,
L2은 가중치의 크기에 비례하여 기울기 값이 구해지지만,
L1는 가중치의 크기와 상관없이 부호만 달라질 뿐 기울기의 크기는 항상 특정 상수로 고정된다.

이는 L1이 sparse parameter를 가지게 된다는 특징과 관련이 있다.
L2는 0과 가까워질수록 기울기 값이 작아지기 때문에 $w \approx 0, w \neq0$ 이지만
L1은 기울기의 크기가 매번 동일하기 때문에 L2 대비 $w=0$이 될 확률이 높다.

조금 더 부연 설명하자면,
L1에서 기울기가 $\pm\,1$일 때 $\text{Initial } w=0.1$이라면 $w=-0.9 \Leftrightarrow w=0.1$를 반복하게 될 것이다.
하지만 우리는 $w$를 업데이트 하기 위해서 Regularizer만 사용하는 것이 아니라
MSE를 같이 사용하기 때문에, 동일한 위치에서 반복만 하는 것이 아니라 $w\approx0$으로 수렴하는 방향으로 움직이게 될 것이다.

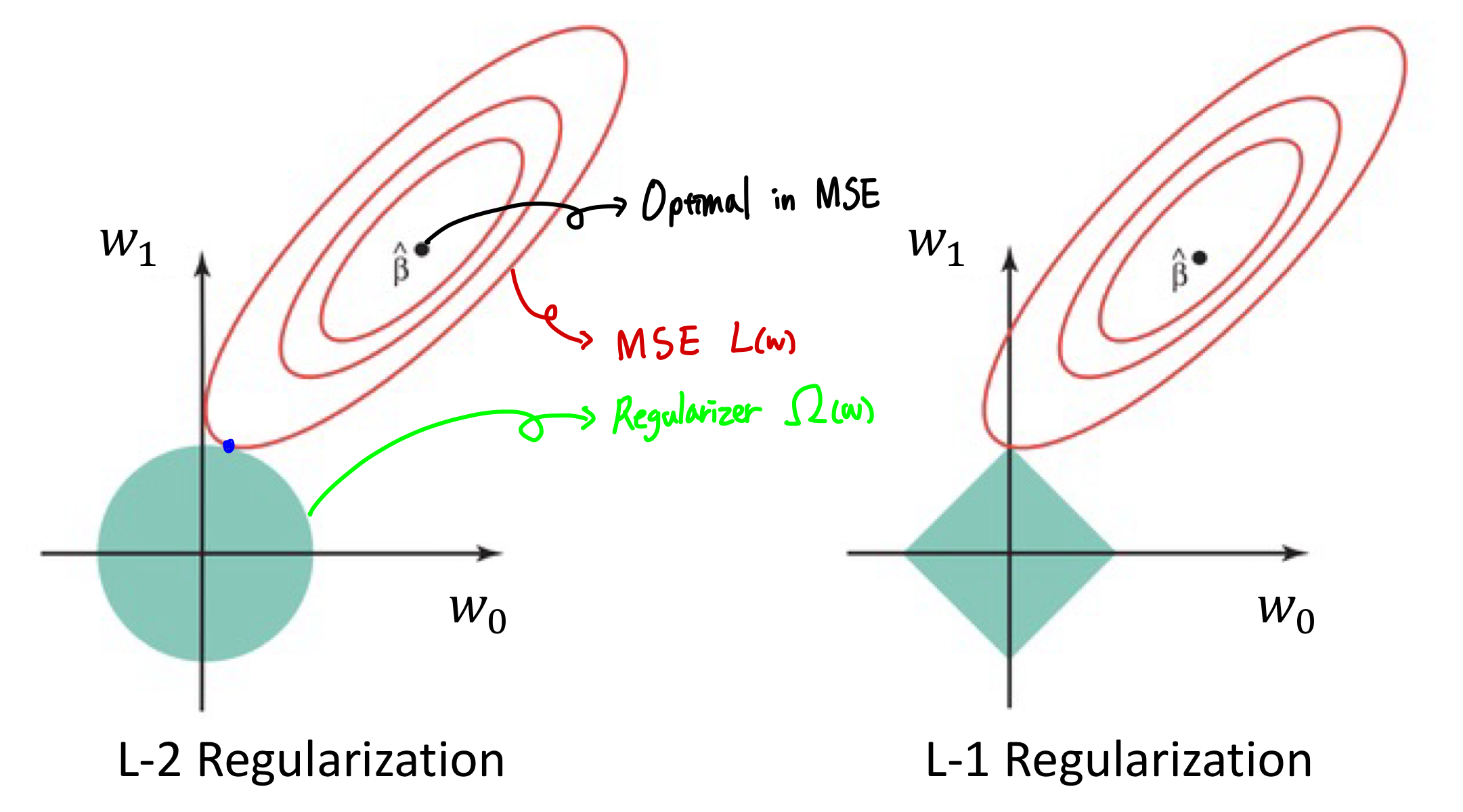
L1과 L2의 기하학적 관점 비교

빨간색이 MSE term 이고, 민트색이 Regularizer 을 표현한 것이다.
MSE term은 항상 타원형 contour를 가진다. 이에 대한 증명은 관련 링크를 남겨놓겠다 (MSE Contour)
그리고 L2는 원형, L1은 다이아몬드 형태를 가지게 된다.

Regularizer를 사용하는 경우 MSE를 최소화하면서 Regulraizer에 대한 제약조건을 만족해야하는데,
그 지점은 아래 MSE와 Regularizer의 접점이라고 볼 수 있다.

그림에서 보다시피 L1을 사용할때는 Regularizer의 꼭짓점에서 접점이 생길 확률이 높은데,
이로 인해 L1 에서는 sparse parameter를 가지게 될 확률이 높다고 볼 수 있다.

다르게 정의하면,
L2는 원의 형태를 띄기 때문에 한 축이 0인 지점에서 접점이 발생할 확률이 낮지만,
L1은 이에 대비 한 축이 0인 지점에서 접점이 발생할 확률이 더 높다고 말할 수 있다.

4) lambda in Regularization

Ridge, Lasso에서는 $\lambda$를 통해서 Regularization의 강도를 조절할 수 있다.

그럼 만약 $\lambda$를 매우 큰 값($\text{ex. } 10^{10}$)으로 설정하면 어떻게 될까?
아래의 예시를 보면 $\lambda$를 큰 값으로 설정하게 되면, $\text{MSE } L(w) \ll \Omega(w)$ 임을 알 수 있다.

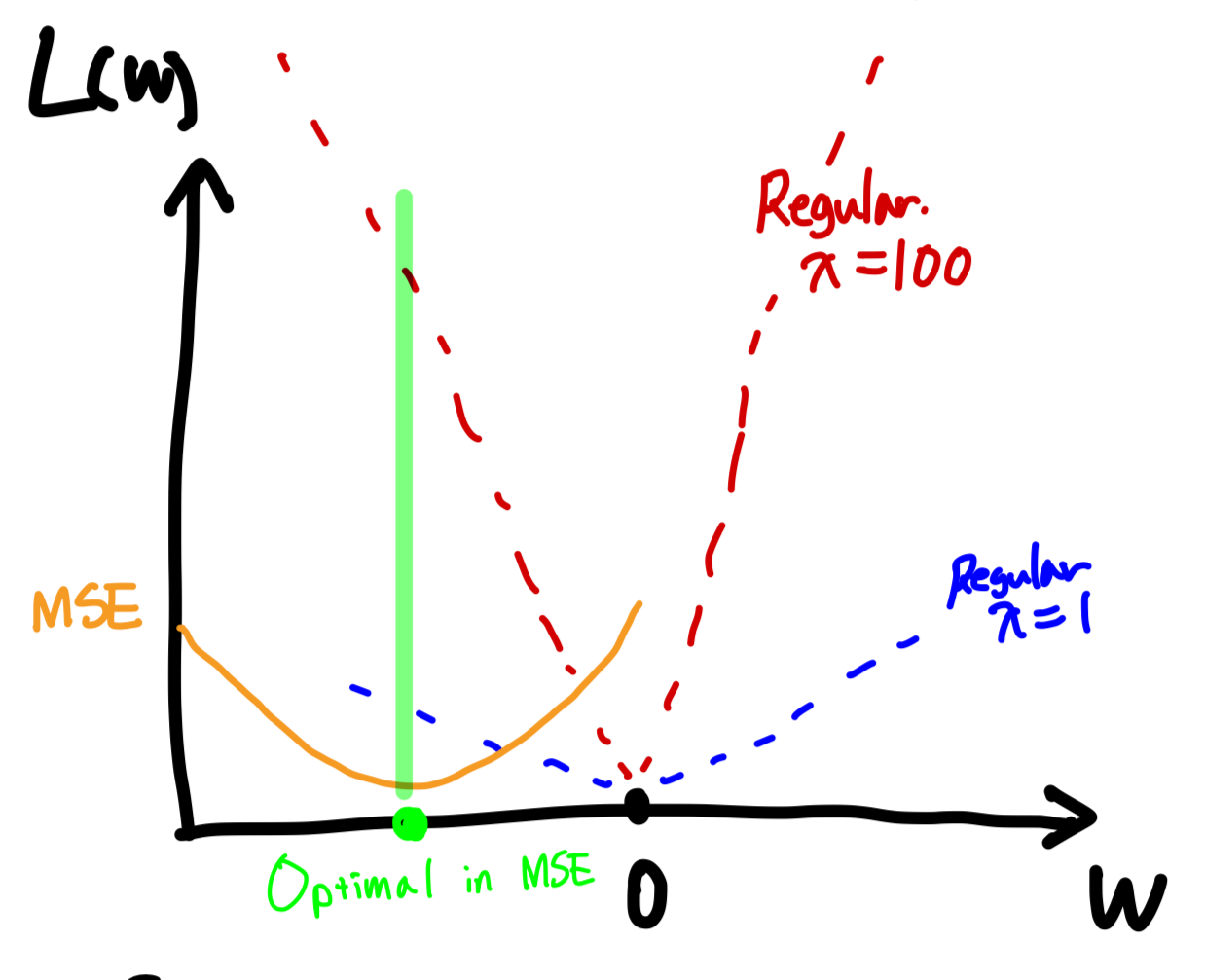
그렇게 되면 $w$를 업데이트 할 때, 실제 데이터를 잘 설명하기보다( $\text{MSE}$ ),
$w$ 가중치($\Omega(w)$)를 줄이는 것을 목적으로 동작하게 될 것이다.

결국 Algorithm에서 Overfitting 은 해결되겠지만, Underfitting 문제가 발생하게 될 것이다.
또한 $\underset{w}{\mathrm{argmin}}(L(w) \,+\, \Omega(w))$을 위해 어느 지점으로 수렴하겠지만,
이는 Algorithm이 제대로 동작함(데이터를 잘 설명하는 것)을 의미하진 않는다.

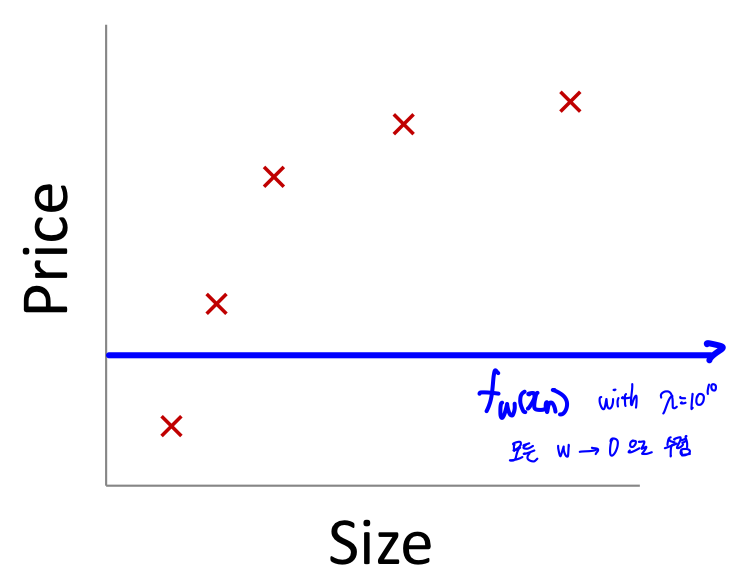
구해진 Mapping function $f_w(x_n)$을 그래프에 표현해보면,
결국 bias($w_0$)을 제외한 모든 $w_i \approx 0$으로 수렴하게 되어 아래와 같이 일직선상의 함수가 그려질 것이다.

---

위의 내용을 다시 정리해보자면,
Underfitting / Overfitting에 대해서 정의하고 Overfittin을 방지하기 위한 Regularization 기법에 대해서 알아보았다. 그런데 우리는 학습된 Model(Mapping Function)이 Underfitting 또는 Overfitting 되었는지 어떻게 알 수 있을까? 다음 글에서 이런 부분을 알아내고 최적의 Model을 선택하는 방법에 대해서 다뤄보려고 한다.