기초인공지능 #3 Heuristic

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.
(2024.03.18 3주차 강의 및 2024.03.25 4주차 강의 일부를 정리한 내용입니다.)

---

Heuristic

먼저 Heuristic에 대해선 간단히 정의하자면 아래와 같다.

1. Heuristic 이란

• 현재 상태가 목표 상태까지 얼마나 가까운지 추정하는 함수
  • Fringe(관심 대상)에 A / B 가 있을때 A가 B보다 더 좋다는 정보를 얻을 수 있음
• 각 탐색 문제에 별도로 설계된 함수

우리는 탐색 문제에서 더 쉽고 빠르게 목표를 찾아내기 위해 Heuristic을 활용한다.
이전 Informed Search 글의 A* Search 설명 부분에서, Admissible Heuristic에 대해서 잠깐 언급하였고 여기에 대해서 좀 더 자세히 설명해보고자 한다.

Admissible Heuristic

1. Admissible Heuristic 이란

Heuristic은 목표 상태까지의 실제 거리를 추정하는 함수라고 말할 수 있다.
하지만 Heuristic, 즉 추정값이 실제값보다 커지게 되면 탐색 알고리즘이 최적해가 아닌 일반해를 찾아가게 될 수 있다는 문제가 있다.
이런 문제를 예방하기 위해 제약이 더해진 것이 Admissible Heuristic이며, 수식으로 표현하면 아래와 같다.

2. Admissible Heuristic 만들기

우리는 최적해를 찾기 위해서 Admissible Heuristic을 사용해야 한다.
그렇다면 우리는 어떻게 Admissible Heuristic을 만들어내고 사용할 수 있을까?

보통 Admissible Heuristic을 생성할 때 다음과 같은 방법을 사용한다.
① 기존 문제를 단순화한 뒤, ② 해당 문제에 대한 Solution을 Heuristic으로 사용한다.

이렇게 만들어지는 Heuristic은 Admissble 하게 만들어지고,
Heuristic의 성능은 값이 실제값을 근사하게 추정할수록 좋은 성능을 가진다고 말할 수 있다.

3. Admissible Heuristic 예시 (8 Puzzle)

하지만 Heuristic을 만들어내는 것은 주어진 문제마다 방법이 달라지기 때문에 한가지로 정의하기가 어렵다. 한번 아래의 예시를 통해서 기존 문제를 어떻게 단순화하고 Heuristic을 찾아내는지 살펴보자.

8개의 숫자 퍼즐이 주어졌을때 퍼즐을 상하좌우의 빈칸으로 움직여 제자리에 위치할 수 있도록 만들어보자.

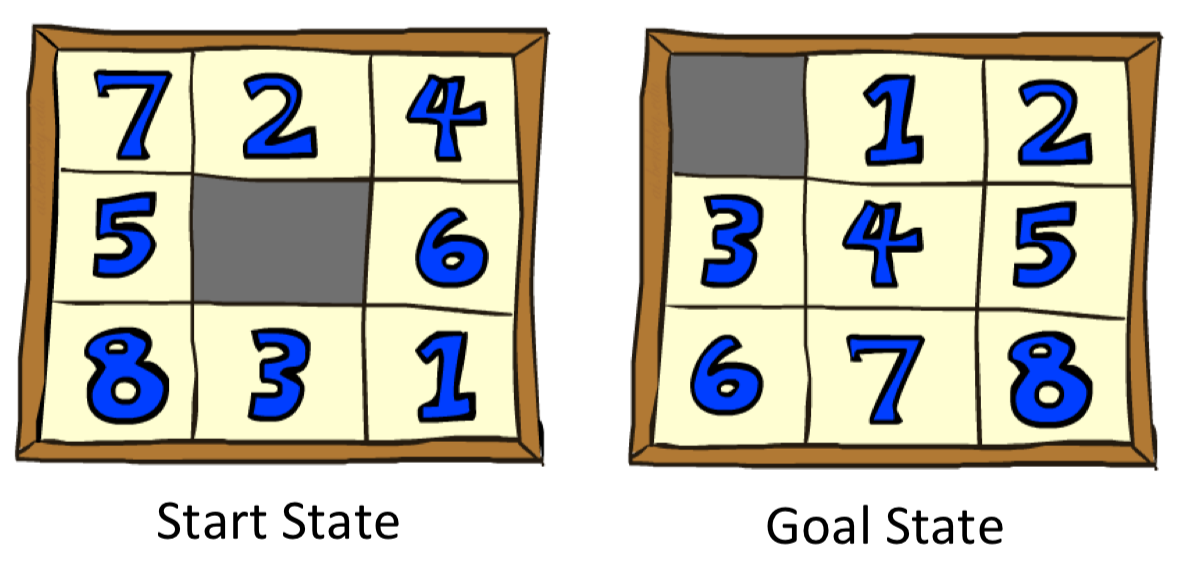
Relaxed Problem : TILES
이런 문제에서 모든 경우의 수를 다 확인하는 것은 쉽지 않다.
그럼 문제를 단순화시켜서, 퍼즐을 빈칸 여부와 상관없이 원하는 위치에 마음대로 이동할 수 있다고 가정해보자.
그렇다면 단순화시킨 문제에서 Solution은 제자리가 아닌 퍼즐의 개수 일 것이다.
(제자리에 위치하지 않은 퍼즐만 한번씩 이동시키면 문제는 해결되기 때문이다.)

단순화 된 문제의 Solution을 A* Search에 적용시키면 다음과 같이 확장되는 Node의 개수를 확연히 줄일 수 있다.

Relaxed Problem : MANHATTAN
Heuristic의 성능은 실제값을 근사하게 추정할 수록 좋아진다고 말했다.
위에서 만들어낸 Heuristic은 과연 좋은 성능이라고 말할 수 있을까?
기존 UCS 대비 확인하는 Node의 개수가 확연히 줄어들긴 했지만, Heuristic이 실제값을 근사하게 추정하지는 않아 보인다.

그럼, 퍼즐을 빈칸 여부와 상관없이 상하좌우 원하는 위치에 마음대로 이동할 수 있다고 가정해보자.
기존 문제는 ① 퍼즐의 상하좌우만 이동이 가능하고, ② 빈칸인 곳으로만 이동이 가능했다.
이 중 ②번에 대한 제약은 무시하고 ①번 제약만 유지하는 식으로 문제를 단순화 시켰다.

이렇게 단순화 시킨 문제에서 Heuristic 값은
1번 타일의 이동거리 + 2번 타일의 이동거리 + ... + 8번 타일의 이동거리와 같다.
이를 통해 우리는 이전의 Heuristic 보다 실제값을 더 근사하게 추정하는 Heuristic을 구했다.

이를 A* Search에 적용시키면, 12 Step 기준으로 이전 대비 확인하는 Node의 개수를 1/3로 줄일 수 있다.

이런 식으로 문제의 제약 조건을 제외하는 방식으로 단순화 시킬 수 있고,
단순화 시킨 문제가 실제 문제와 유사한 만큼 우리는 좋은 Heuristic을 얻을 수 있다.

4. Heuristic의 계산 복잡도

그런데... 확인하는 Node 개수를 줄이면 줄일 수록 우리에겐 좋은걸까?
위 예제의 TIELS, MANHATTAN 방식을 비교해보면 MANHATTAN Heuristic의 성능이 더 좋지만 계산량이 더 많은 것을 알 수 있다.

이처럼, Heuristic 추정치의 질과 계산량은 서로 Trade-off 관계에 있다.

Consistent Heuristic

1. Admissible Heuristic in Graph

Graph 구조에서는 Cycle(순환 구조)이 발생할 수 있다.
이런 구조에서 탐색을 하면 어떻게 될까? 운이 좋다면 답을 찾을 수 있겠지만 탐색을 무한히 반복하는 경우도 있을 것 이다.
이런 문제를 방지하기 위해서 탐색에서는 기본적으로 이전에 확인했던 Node는 다시 확인하지 않는다.

그렇다면 아래 예시를 통해 이전에 확인했던 Node를 확인하지 않을 때,
Admissible Heuristic을 사용한 A* Search에서 생길 수 있는 문제점을 확인해보자.

위의 예시에서 S 에서 시작해서 G 를 찾아가보자.
$f(n) = g(n) + h(n)$ 값이 작은 Node를 먼저 확인하기 때문에 S → B → C 순으로 먼저 확인한다.
그리고 $f(G) =6,\,f(A)=5$ 이기 때문에 S → B → C → A 순으로 확인하게 된다.

그렇지만 A를 거쳐 C로 가는 경로는 확인할 수 없다. C는 이미 B 경로를 통해 확인했기 때문이다.
결국 최종적으로 찾게 되는 해는 S → B → C → G 이고, 이는 최적해가 아니다.
이렇듯 Admissible Heuristic을 사용하게 되면 Graph 구조에서 Optimal 이 보장 되지 않는다.

2. Consistent Heuristic 이란

Heuristic 조합

1. Heuristic 조합의 필요성

Heuristic의 값이 0에 가까울수록 탐색 성능이 떨어지고 (ex. UCS ≈ A* Search with Heuristic close to 0)
Heuristic의 값이 실제값에 가까울수록 계산량이 많아진다.

이런 Trade-off 관계로 어느 하나만을 선택하기 어려울 때,
우리는 성능이 낮은 Heuristic 여러개를 조합하여 사용해볼 수 있다.

8 Puzzle 예시에서 사용했던 TILES Heuristic이 $h_{tiles}$, MANHATTAN Heuristic이 $h_{man}$일 때,
$h_{man}(n) \geq h_{tiles}(n)$ 이라고 말할 수 있다.
이처럼 모든 상태에서의 값을 비교했을 때, 어느 한쪽의 Heuristic의 값이 모두 크거나 같을 때 Dominance라고 말할 수 있으며 이런 경우에는 1개의 Heuristic만 을 사용하는 것이 더 정확하다.

하지만 Dominance가 아닐 때는 어떨까?
1개의 Heuristic이 모든 경우에 크거나 같지 않은 2개의 Heuristic $h_a, h_b$가 있다면,
우리는 2개 Heuristic 값 중 실제값에 더 가까운, 즉 최대값을 취하는 방식으로 이를 활용할 수 있다.

위와 같은 방식을 활용하여, 우리는 계산량이 낮지만 Dominance 하지 않은 여러개의 Heuristic을 조합함으로써 성능을 높일 수 있다.

2. Heuristic 조합 예시 (Knight`s moves)

아래의 체스판에서 Knight를 최소한의 움직임으로 빨간 점으로 도달시키는 경로를 구하는 문제가 주어졌을 때, 우리는 어떻게 Heuristic을 만들 수 있을까?

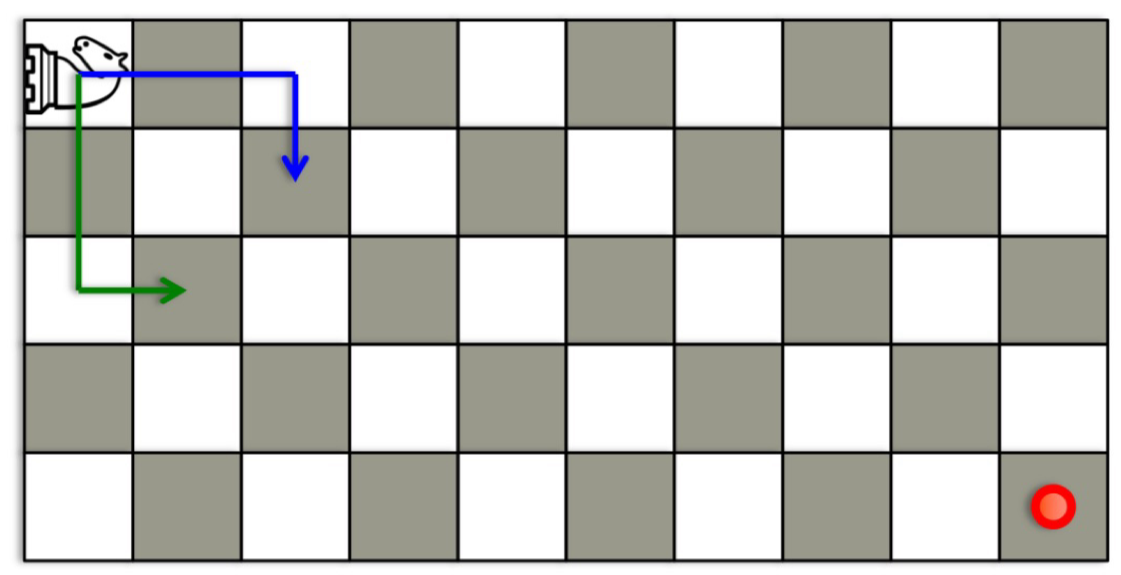
① $h_1 = \textbf{round}(\text{Manhattn Distance} \;/\; 3)$
② $h_2 = \textbf{round}(\text{Euclidean Distance} \;/\; \sqrt{5})$
③ $h_3 = \textbf{round}(\text{Max(x shift, y shift)} \;/\; 2)$
위와 같이 3개의 Heuristic을 생각해볼 수 있고, 조합해서 아래와 같은 Heuristic을 만들어 낼 수 있다.

이렇게 우리는 문제를 단순화 시킴으로써 Heuristic을 만들어 낼 수 있고,
여러개의 Heuristic을 조합하는 방식을 통해서 성능이 더 좋은 Heuristic을 만들어 낼 수 있다.
이렇게 만들어낸 Heuristic을 활용하여 탐색 문제를 더 효율적으로 풀어낼 수 있다.