이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.
Local Search
1. 정의
이전까지의 Search problem에서 Solution은 Goal state를 가기 위한 path 였었다.
하지만 많은 최적화 문제에서는 path는 상관 없이 Goal state 자체가 Solution 이다.
이러한 탐색 문제를 우리는 Local Search 라고 정의한다.
Local Search에서는 반복적인 개선을 통해서 Solution을 구하는데,
여러가지 방법론에 대해서 본 글에서 설명하고자 한다.
2. 예시
Local Search에 대한 대표적인 예시로,
N-queens 문제(NxN 체스판에 서로 겹치지 않도록 N개의 Queen 배치)가 있다.
N-queens 문제에서 Solution은 N개의 Queen을 배치하는 과정이 아닌, N개의 Queen 배치 그 자체이다.
Hill Climbing
Hill Climbing은 가장 간단하고 일반적인 방법론이며, Greedy한 성격을 가진 Algorithm이다.
1. 정의
Hill Climbing은 아래와 같이 동작한다.
① Random한 위치에서 시작한다.
② 현재의 상태보다 더 나은 근접한 상태로 이동을 반복한다.
③ 현재의 상태보다 더 나은 근접한 상태가 없다면 종료한다.
Pseudo Code

2. 문제점 및 해결 방안
Hill Climbing의 Greedy한 접근방식으로 인해 아래 2가지 문제점이 존재한다.
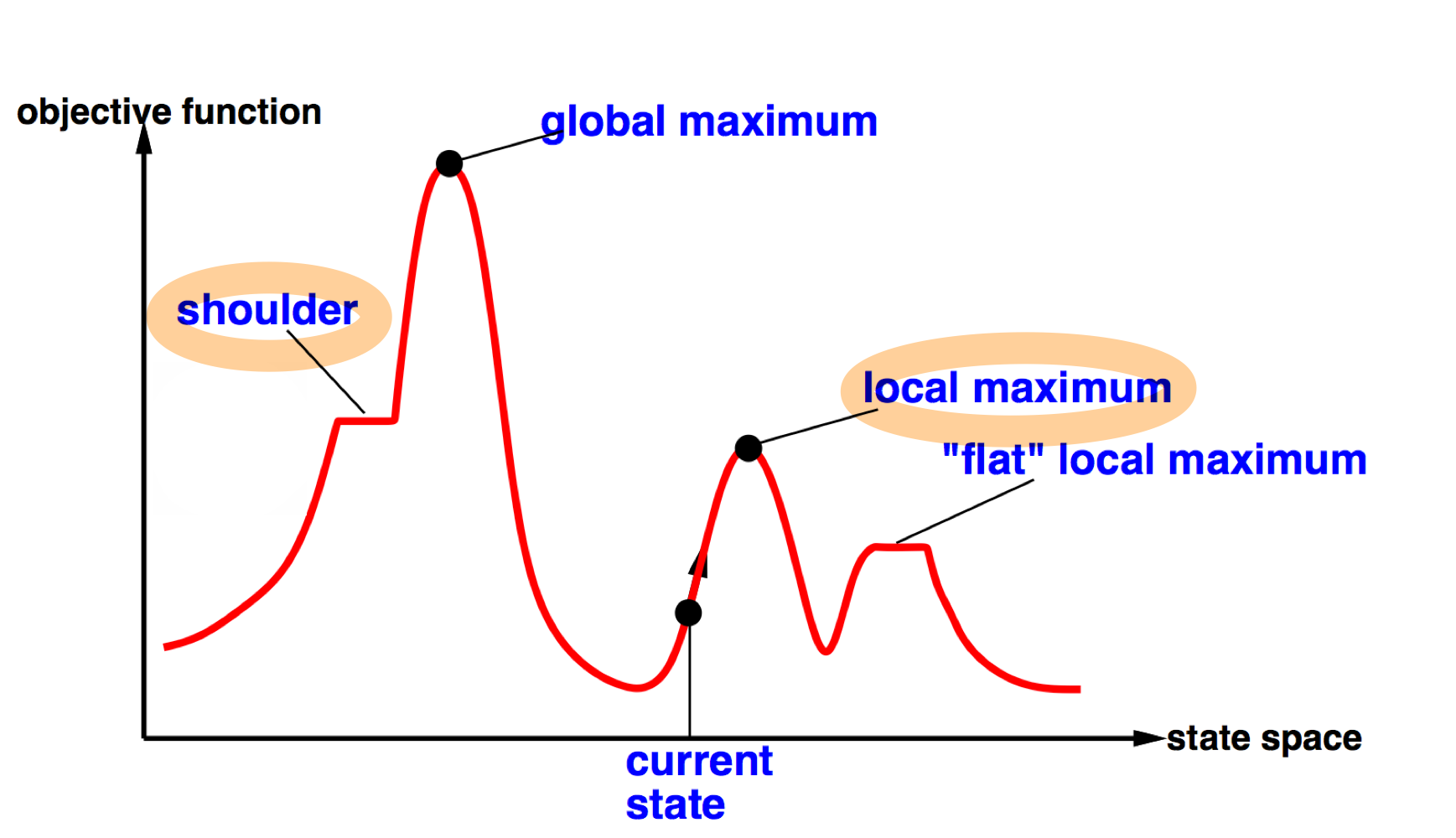
1️⃣ Local maximum
문제점 : Global maximum을 보장하지 못함
근접 상태를 통해 종료 여부를 판단하기에, Local maximum을 종료 위치로 판단할 수 있다.
해결 방법 : Random restart
여러 시작점에서의 Solution을 구하고 이를 통해서 Global maximum을 찾아낼 수 있다.
2️⃣ Shoulder
문제점 : Shoulder(평평한 지점)을 탈출하지 못함
해결 방법 : Random sideways moves
특정한 경우에 랜덤하게 특정 방향으로 이동시키는 방법을 통해 평평한 지점을 탈출하고 maxmimum을 구할 수 있다.
3. 예시
8-Queens 문제에 Hill Climbing Algorithm을 적용하여 해결해보자.
위에서 말한 문제점을 개선하지 않았을 때, 개선했을 때를 비교해 볼 수 있다.
1️⃣ No sideways moves
- 성공 확률 : 14%
- 이동 횟수 평균 : 성공 시 4번 / 실패 시 3번
- 이동 횟수 기댓값 : 약 22번
2️⃣ Allowing 100 sideways moves
- 성공 확률 : 94%
- 이동 횟수 평균 : 성공 시 21번 / 실패 시 65번
- 이동 횟수 기댓값 : 약 25번
Shoulder 지점을 탈출하기 위해 Side moves를 허용하면 성공할 확률이 늘어나지만,
이동 횟수에 대한 기댓값을 살펴보면 허용하지 않은 경우가 더 낮은 것을 알 수 있다.
이를 통해 무조건적으로 Side moves를 허용하기보단 사용하지 않거나 횟수를 적절히 조절하는 것이 필요함을 알 수 있다.
Simulated Annealing
Hill Climbing이 문제점(Local minimum, Shoulder)을 해결하기 위한 방법이 Simulated Annealing 기법이다. 이 원리는 금속을 가열한 뒤 천천히 냉각시키며 결정을 성장시키는 방법을 통해 결함을 줄이는 Annealing 기법으로부터 착안됐다. Simulated Annealing 기법은 아주 가끔씩 안 좋은 방향으로 이동하는 것을 허용함으로써 Local minimum을 탈출하고 Global minimum을 찾는 방법이다.

위의 Psuedo Code를 보면,
next current 인 경우에도 확률에 따라 next로 이동함을 알 수 있다.
다만 T는 시간에 따라 낮아지는데, 이를 얼마나 천천히 낮출 것인지에 따라 Global minimum를 찾을 수 있는지가 결정된다. 따라서 T를 얼마나 천천히 낮출 것이냐는 굉장히 어려운 문제이다.
※ 설명
이므로, 일 때 이다.
그럼 일 때 를 가지게 되고,
에서 T가 클 땐 1에 가까워지고, 작을 땐 0에 가까워진다.
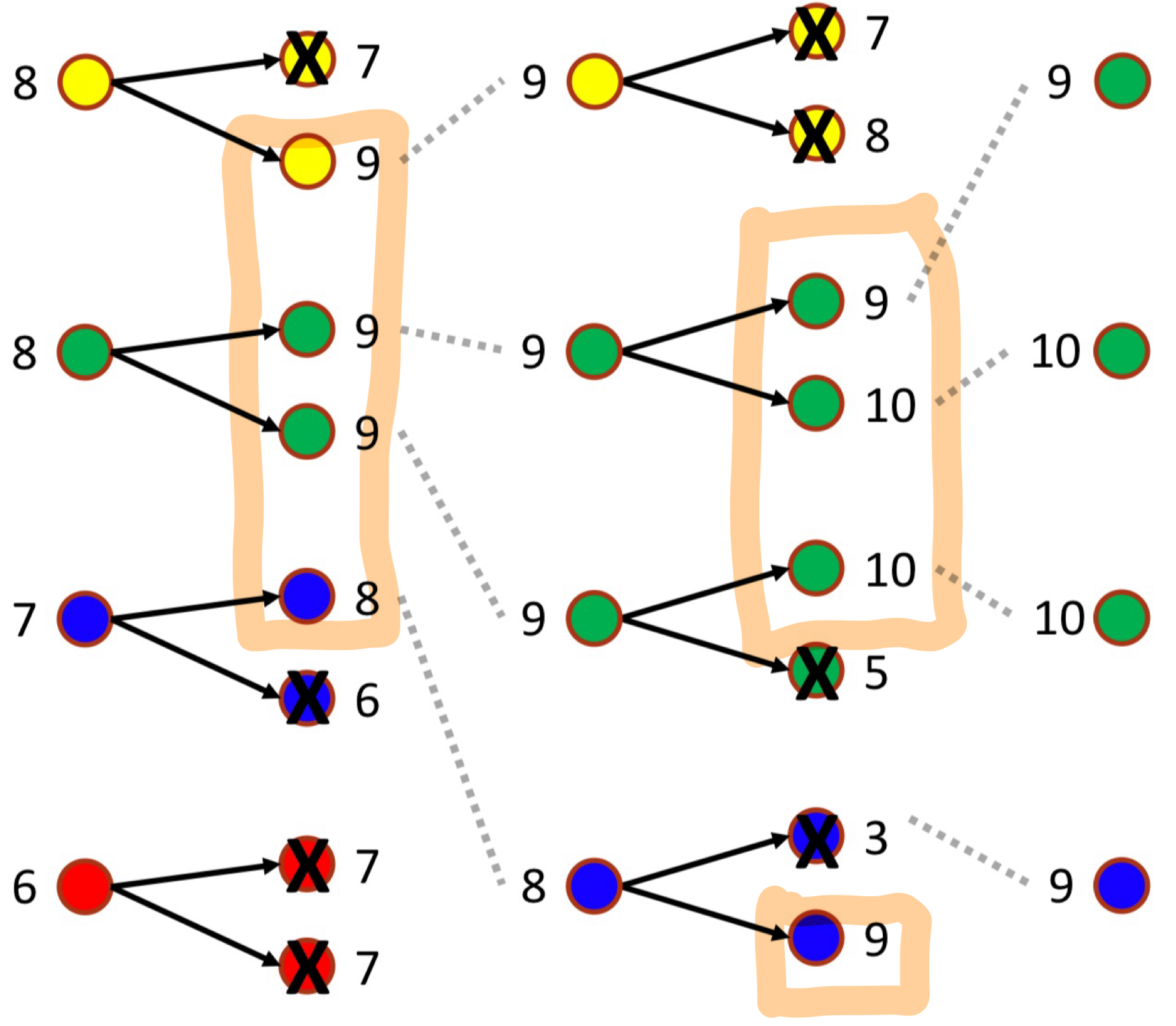
Local Beam Search
Local Beam Search는 K개의 Local search algorithm을 각각 랜덤한 Initial point에서 수행하되, Algorithm의 각 Step에서의 결과를 공유하여 결과가 가장 우수한 K개의 상태를 선택하고 다음 Step을 진행하는 방법이다.
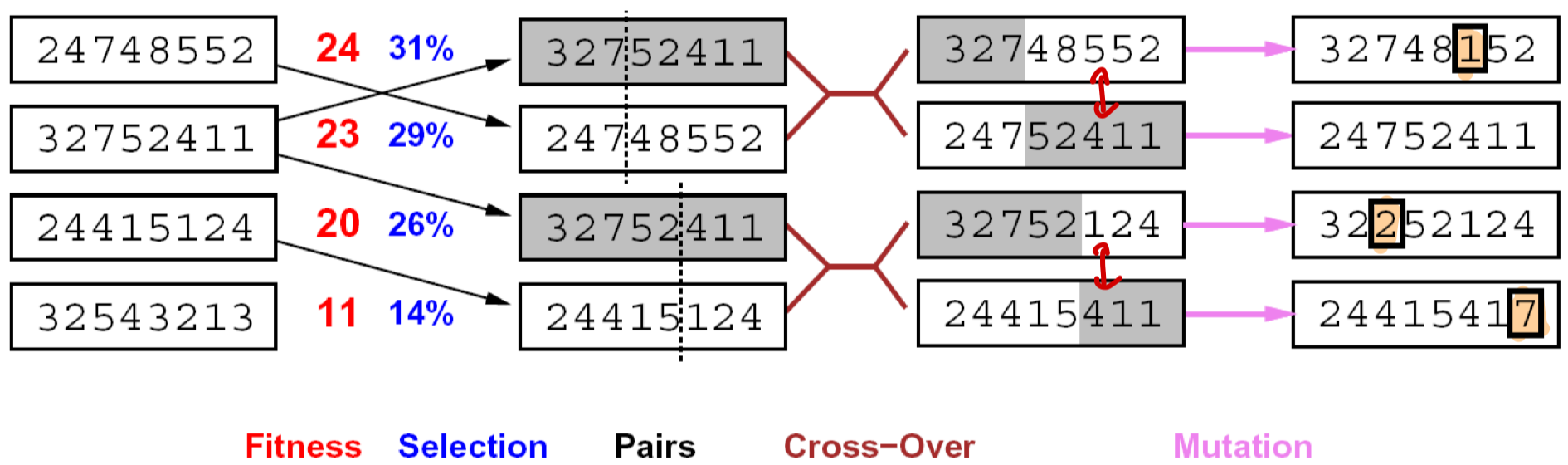
Genetic Algorithm
Genetic Algorithm은 각 Step에서 K개의 샘플을 고르고 유전자 조합이 일어나듯이 일부 가공을 통해 새로운 상태를 만들고 이로써 최적해를 찾는 기법이다.
Algorithm의 순서는 아래와 같이 진행된다.
Fitness(적합도 판단) → Selection(샘플 선택) → Pairs(매칭) → Cross-Over(섞기) → Mutation(변형)