기초인공지능 #8 Naive Byes

이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.

---

Naive Bayes

Naive Bayes 모델은 확률에 기반한 분류 기법으로, 조건부 확률을 이용하여 주어진 데이터의 클래스(Y)를 예측하는 모델이다.

1. Naive Bayes의 기본 개념

Naive Bayes를 이해하기 위해 필요한 핵심 개념은 독립 가정과 조건부 확률 2가지를 말할 수 있다.

독립 가정

Naive Bayes에서는 주어진 특징 $F_1,\,F_2,\,\dots,\,F_n$들은 서로 독립이라고 가정한다.
각 특징들은 주어진 클래스 Y에 종속적이고 서로 독립적으로 발생한다고 가정하기 때문에 계산이 단순해진다.

조건부 확률 - 베이즈 정리

또한 Naive Bayes에서는 클래스를 예측하기 위해,
벡터 $\mathbf{F}$가 주어졌을때 클래스 Y의 확률인 $\text{P}(Y|\mathbf{F})$를 계산한다.

이를 계산하기 위해서 베이즈 정리를 활용하는데
아래 수식의 우측에 있는 값들은 우리가 데이터를 통해서 구할 수 있는 값이고, 이를 통해서 좌측의 우리가 구하고자 하는 확률값을 구할 수 있다.

2. Naive Bayes의 훈련/예측 과정

실제로 Naive Bayes가 어떤 과정을 통해서 클래스를 예측하는지 알아보자.
아래의 훈련 데이터가 있고, 사용할 특징으로는 $F_1$ 주소록 등록 여부, $F_2$ FREE 단어 빈도라고 가정해보자.

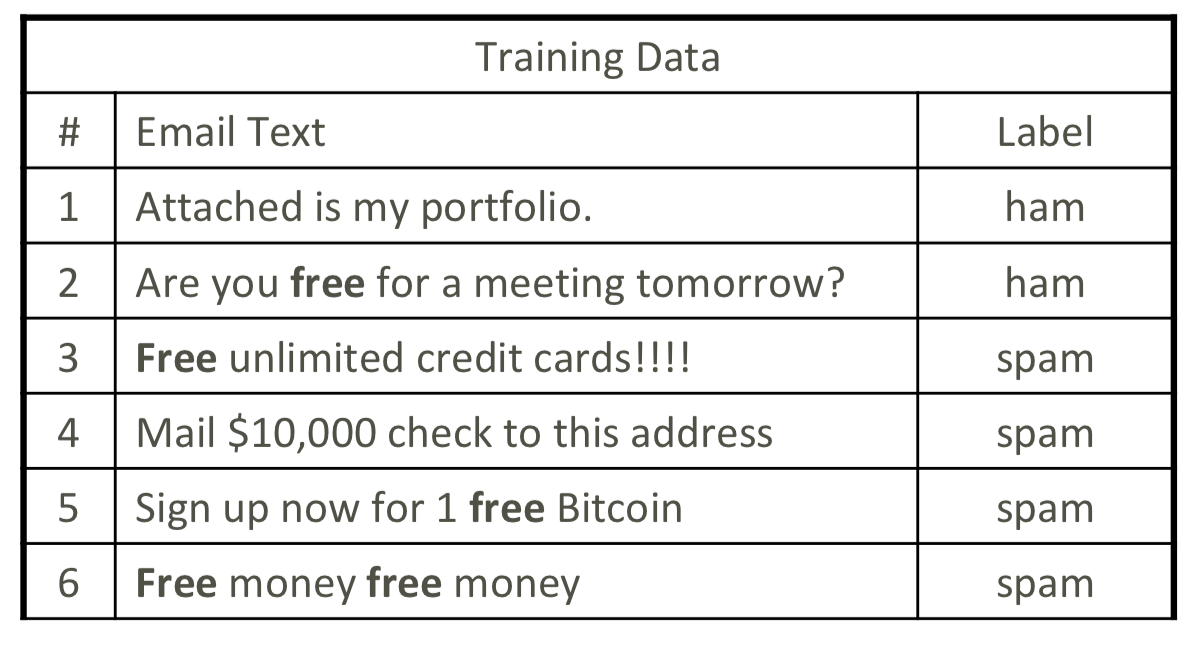
Step 1) 확률 추정

확률 추정에서는 ① 사전 확률과 ② 각 특성에 대한 조건부 확률을 구한다.
사전 확률은 $\text{P}(Y)$, 각 특성에 대한 조건부 확률은 $\text{P}(F_i|Y)$ 이다.

위의 확률들을 구해서 아래의 probability table을 채워넣을 수 있다.

Step 2) 모델 예측 (Classification)

위에서 구한 확률을 가지고 이제 우리가 찾고자 했던 $\text{P}(Y|\mathbf{F})$를 구할 수 있고,
이는 클래스의 사전 확률과 각 특성들의 조건부 확률의 곱으로 구할 수 있으며 아래 수식과 같다.

알고 있는 사람에게서 "Free food in Soda 430 today" 라는 메일이 왔을 때,
위에서 구한 확률을 통해 이 메일이 스팸인지 아닌지 분류해보자.

각각의 특징은 $F_1 =\text{yes}, \,F_2=1$과 같고, 결합 확률을 구하면 아래와 같다.

해당 특징이 각 클래스에 해당할 확률값을 Normalize 하면 아래와 같이 계산할 수 있고,
즉 스팸에 해당할 확률이 14%, 그렇지 않을 확률이 86%이다.

Naive Bayes는 이렇게 주어진 데이터를 확인하여 확률(사전확률/조건부확률)을 구하고,
이를 베이즈 정리를 통해 주어진 특징이 클래스에 해당할 확률을 구함으로써 예측하게 된다.

Maximum Likelihood

Likelihood

먼저 Likelihood(가능도 또는 우도)에 대해서 알아보고 넘어가자.
보통 가능도에서 설명할때 확률과 비교해서 설명하는데, 각각의 정의는 아래와 같다.

• Probability (확률) : 주어진 확률분포가 있을 때, 관측값 혹은 관측 구간이 분포 안에서 얼마의 확률로 존재하는 지를 나타내는 값
  $\text{확률} = P(\text{관측값 }\, X\,|\,\text{확률분포 }\, D)$
• Likelihood (가능도) : 어떤 값이 관측되었을 때, 해당 관측값이 어떤 확률분포로부터 나왔는지에 대한 확률
  $\text{가능도} = L(\text{확률분포 }\, D\,|\,\text{관측값 }\, X)$

가능도에서는 관측값이 고정이 되고, 이 관측값이 각각의 확률분포에 해당할 가능도를 구하는 것이다.
예를 들어 1 이라는 관측값이 나왔을 때, ① 평균이 0인 정규분포와 ② 평균이 1인 정규분포에 해당할 가능도를 구해보면 ②에서의 가능도가 더 높게 나올 것이다.

참고 자료 : https://jjangjjong.tistory.com/41

Maximum Likelihood

Maximum Likelihood는 위에서 말한 가능도를 최대가 되게 하는 확률 분포를 찾는 작업이다.

우리는 probability table을 채워넣기 위해서 주어진 데이터에서 각 항목별 비율을 구했었다.
다만 이러한 과정을 수식적으로 표현하여 구할 수 있다.

먼저 여기서는 $\theta$ 변수를 활용하는데, 이전에 구했던 사전/사후 확률을 표현하는 변수이다.
$\theta$를 구하기 위해서는 $P(\text{observation}|\theta)$을 구해야 한다.

간단한 예시와 함께 설명해보자면,
구슬을 3개 골랐는데 2개는 빨간색이고 1개가 파란색이라는 관측 결과가 나왔고,
이 때 구슬 1개를 고를 때 빨간색일 확률을 구한다고 생각해보자.

이는 $P(\text{red}|\theta)P(\text{red}|\theta)P(\text{blue}|\theta)$ 와 같을 것이고 이에 대한 확률 값은 $\theta^2(1-\theta)$ 일 것이다.
즉 우리는 $\argmax_{\theta} \theta^2 (1 - \theta)$를 구해야하고, 최적점을 찾기 위해 미분을 이용한다.
이때 미분 시의 계산을 용이함을 위해 Log를 사용한다. $\Rightarrow \argmax_{\theta} \ln (\theta^2 (1 - \theta))$
이를 Maxium log-likelihood 라고도 말한다.

관측값을 통해 얻어진 확률식을 미분하여 확률 값을 추정해보면, 아래와 같이 구할 수 있다.

Overfitting

다만 위의 방식을 그대로 사용하면, 주어진 데이터에 과적합 된다는 문제점이 있다.
이를 위해 Smoothing 기법을 사용하는데 여기에 주로 사용되는 방법이 바로 Laplace Smoothing이다.

❗️ Laplace Smoothing

Laplace Smoothing이 적용되지 않았을 때 조건부 확률을 아래와 같이 구할 수 있을 것이다.
$c(x)$는 해당 경우가 발생한 횟수, $N$은 전체 발생 횟수이다.

Laplace Smoothing은 모든 이벤트가 1번씩은 발생했다고 간주하는 것이고,
1번이 아니라 $k$번을 사용하는 경우도 있다.