컴퓨터 구조 #1 Performance

이 글은 김영근 교수님의 컴퓨터 구조 강의를 듣고 정리한 내용입니다.

---

아래 본문에서는 컴퓨터의 성능에 대해 다루고자 한다.
그 전에, 컴퓨터는 어떤 부품들로 이루어졌는지 한번 짚고 넘어가려고 한다.

아래는 iMac Pro를 해체한 모습인데, 보다시피 CPU / Main Memory(DRAMs)가 포함되어 있다.
다른 컴퓨터도 마찬가지로, CPU / Main Memory는 필수적으로 포함되어 있으며
각각의 목적에 따라 다양한 Input / Output 기기들을 추가로 사용하는 것을 볼 수 있다.

즉 아래에서 언급하는 컴퓨터 → CPU / Main Memory 라고 볼 수 있다.

컴퓨터의 성능

그렇다면 우리는 컴퓨터의 성능을 어떻게 정의할 수 있을까?
어떤 컴퓨터가 가장 좋다고 말하기 위해서는, 먼저 성능에 대한 기준이 있어야한다.

성능에 대한 여러 가지 지표를 생각해보면 Processor 속도 / Memory 크기 등이 있을텐데,
계층(목적)에 따라 주요한 성능 지표를 나타내면 아래 그림과 같다.

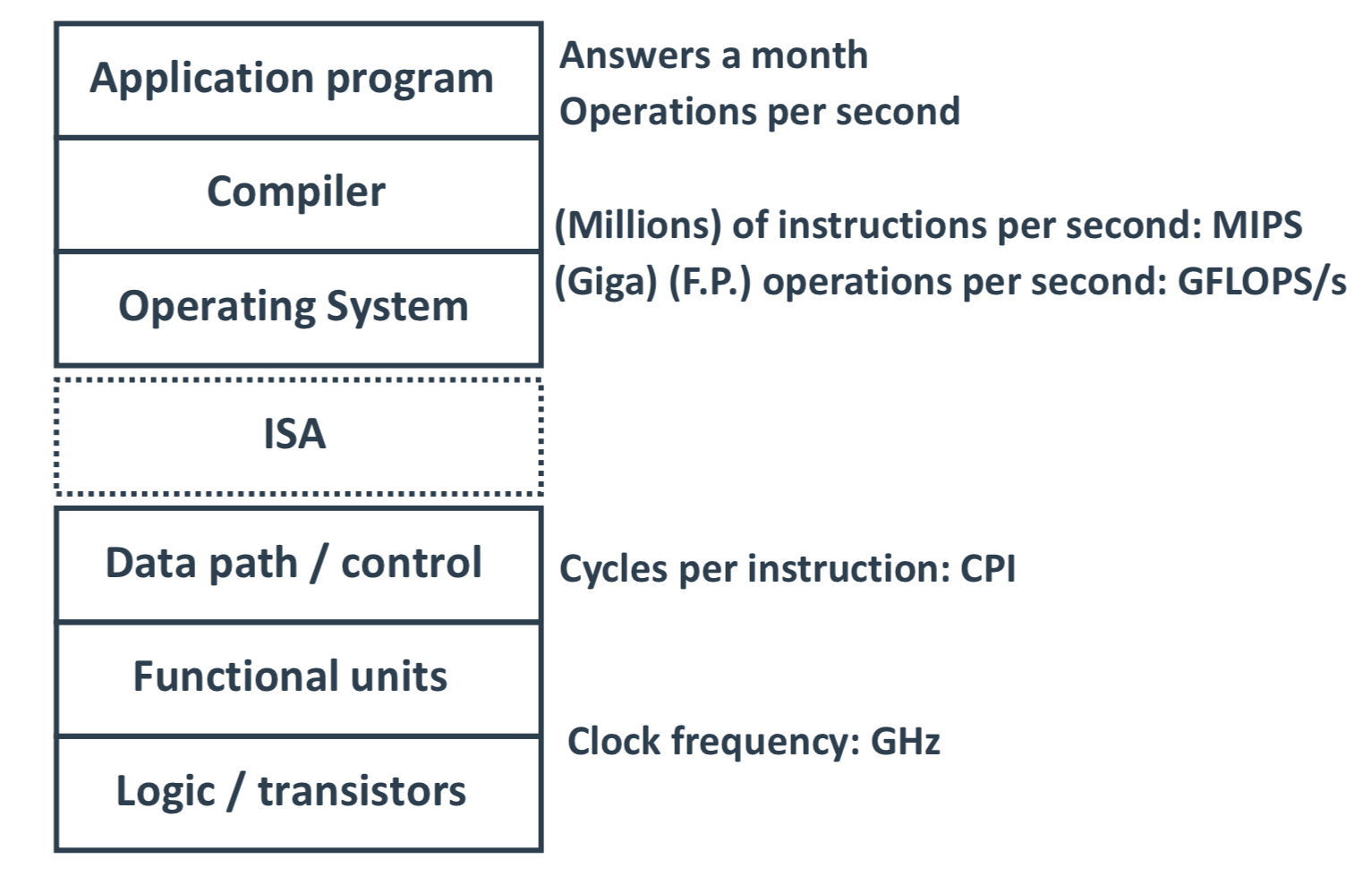
위에서부터 살펴보면 답변의 주기, 초당 명령어 수, 초당 연산 수, 명령어 당 Cycle 수 등이 있는데
이러한 성능 지표들의 공통점은 시간이 얼마나 빠르냐 이다.

성능 지표 - 실행 시간

그렇다면 CPU의 성능 지표로써 실행 시간(execution time)을 사용할 수 있을 것이다.

그럼 이러한 실행 시간을 어떻게 구할 수 있을까? 물론 직접 실행시켜본다면 알 수 있겠지만,
실행 환경이 없다든지 또는 시간이 너무 많이 소요된다던지와 같은 이유로 실행 시간을 사전에 계산할 수 있다면 좋을 것이다.

이러한 실행 시간을 계산하기 위해, 먼저 CPU가 어떻게 동작되는지 알아야 할 것이다.

CPU 동작

CPU는 데이터를 불러오고, 불러온 데이터에 여러 연산을 수행하고 다시 저장하는 과정을 반복한다.
이때 Clock을 통해 여러 연산들의 실행 시점을 동기화하여 충돌 없이 순차적으로 실행되게끔 하는데,

Clock이 짧을수록 다음 연산으로 넘어가는 속도가 빨라지고 전체 실행 속도가 빨라진다고 할 수 있으며, 이런 Clock의 속도를 아래와 같이 표현할 수 있다.

• Clock Cycle Time
  아래 그림과 같이 상승/하강 Pulse로 이루어진 1개의 주기를 Clock Cycle Time이라고 한다.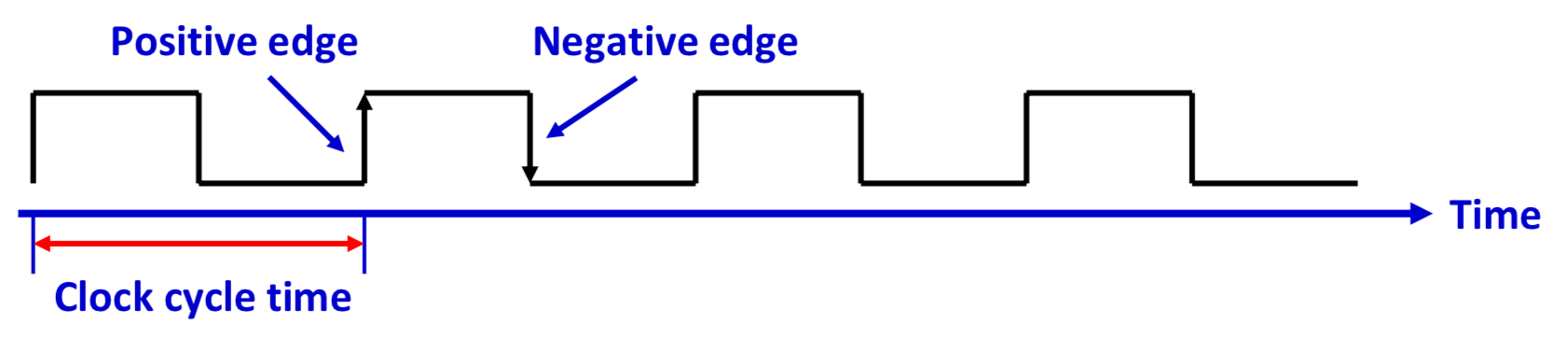

  

• Clock Rate
  Clock Cycle Time의 역수를 Clock Rate 라고 말하며, 1초당 Clock 수를 의미한다.

※ Clock Cycle Time은 어떻게 정해질까?
CPU의 연산(≠ 명령어)은 어떤 Storage 개체에 변화가 생기는 작업을 의미하는데,
이러한 작업 중 가장 긴 시간이 걸리는 연산 작업에 의해 Clcok Cycle Time이 정해진다.

계산 방법 ① Clock cycles 수

그렇다면 이제 위해서 말했던 Clock을 통해 실행 시간(Execution time)을 계산해보자.
작성한 프로그램은 CPU의 여러 연산 작업을 수행할 것이고, 실행 시간은 아래와 같이 구할 수 있을것이다.

Clock cycle time은 우리가 사용하는 CPU 제품의 정보에서 알 수 있을 것이다.
그러나 우리가 작성한 프로그램에 필요한 Clock cycle의 수는 어떻게 알 수 있을까?
사실 이를 구한다는 것은 굉장히 어려운 작업일 것이다.

계산 방법 ② CPI

그래서 좀 더 현실적인 방안으로, CPI(Cycles Per Instruction)를 이용하는 방안이 있다.
CPI는 명령어에 필요한 Cycle의 수를 의미하는데,
우리가 여러 종류의 명령어를 사용한다면, 명령어별 평균을 통해 CPI를 구할 수도 있다.

그렇다면 실행 시간은 아래와 같이 구할 수 있는데,
Instruction의 수는 작성한 프로그램을 컴파일 했을 때 나오는 low level code를 통해 보다 손쉽게 알 수 있고, CPI 또한 제조사 등을 통해서 알 수 있는 정보이다.

그럼 우리는 위의 식을 통해 성능을 높이기 위해서는(≈ 실행시간을 낮추기 위해서는),
① 명령어의 수 줄이기, ② CPI 낮추기, ③ Clock cycle time 감소와 같은 방법이 있음을 알 수 있다.

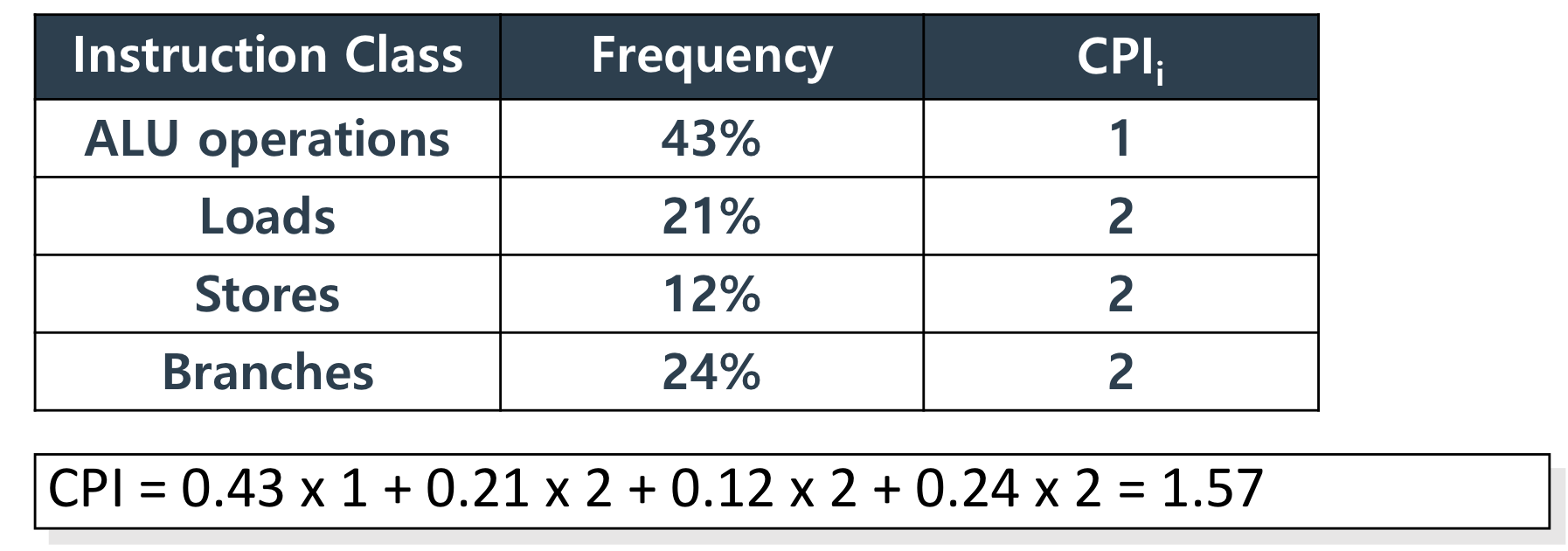
※ CPI 계산
CPI의 계산 공식은 아래와 같고, 이에 대한 예시이다.

※ CPU 성능에 대한 여러 관점

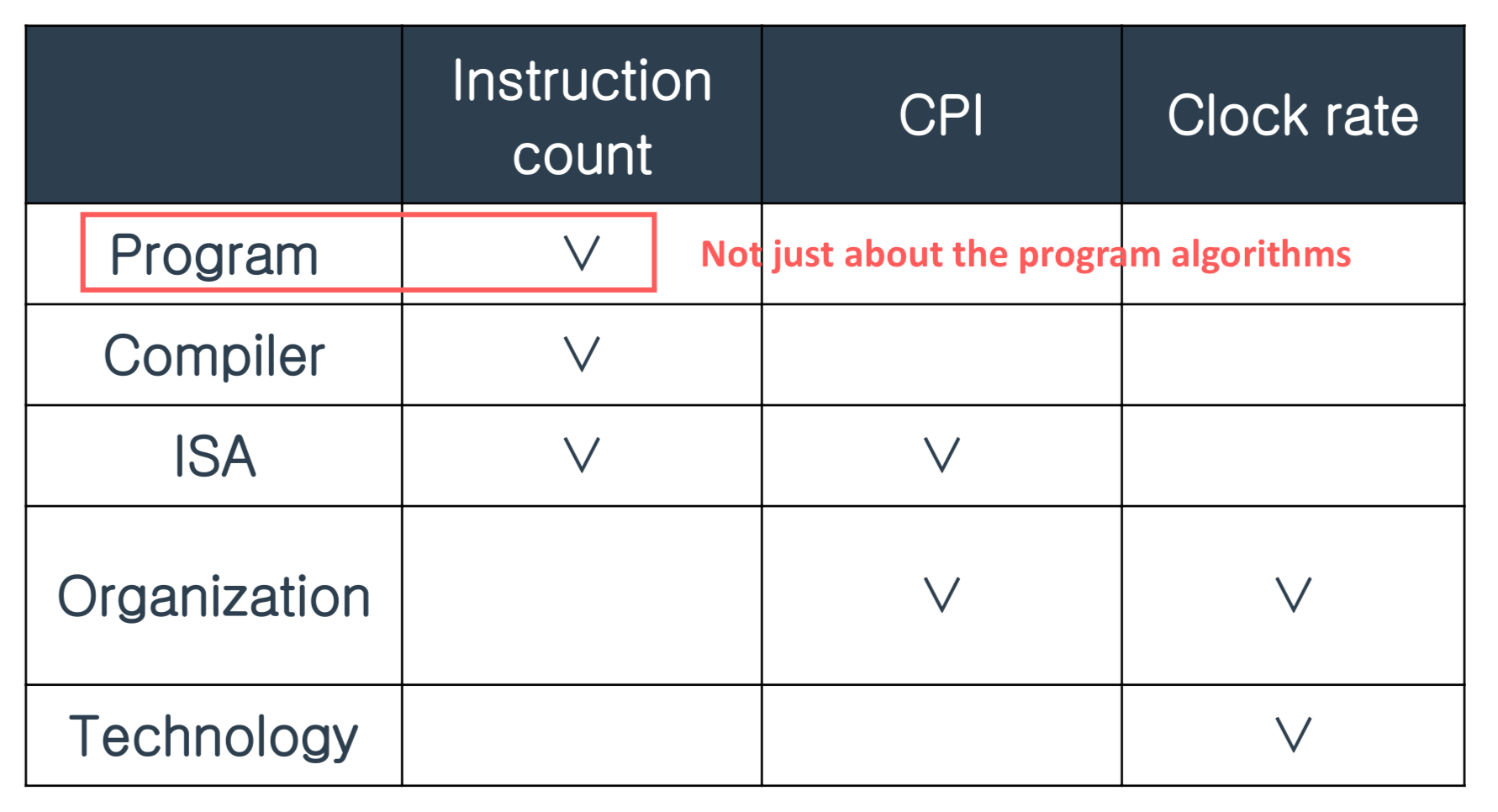
성능을 높이기 위해 할 수 있는 방법들과 관련되어 있는 계층을 표로 나타내면 아래와 같다.
우리가 실제로 접근할 수 있는 영역은 Program 이며, 이 외에 Compiler/ISA 등은 직접적으로 제어할 수 있는 영역은 아니다. (Technology = Transistor의 집적 기술 등 ...)

우리는 성능을 높이기 위해서 Program 수정으로 필요한 명령어 개수를 직접적으로 조절할 수 있을 것이고,
이러한 명령어 개수 조절을 통해 CPI에도 간접적으로 영향을 미칠 수 있을 것이다.

성능 지표 - MIPS , FLOPS

실행 시간 외에도 다른 성능 지표들이 있는데, 그 중 MIPS와 FLOPS에 대해서 잠깐 언급하려고 한다.

MIPS

MIPS(Million instructions per second)는 이름 그대로
초당 실행 되는 백만개 단위의 명령어의 수를 의미하고, 수식은 아래와 같다.

다만 MIPS는 명령어별 복잡성(CPI)을 고려하지 않기 때문에 실제 성능과는 다른 결론을 내릴 수 있다.

때문에 MIPS는 CPU 보단 Kernel(운영체제)의 성능을 확인할 때 주로 쓰이는데,
Kernel에서는 ① 시스템 호출 또는 단순 명령어 처리 위주의 동작을 하므로 명령어별 복잡성을 고려하지 않아도 되고, ② Kernel은 다른 H/W (Architecture-Intel/ARM)에서 실행될 수 있는데, 명령어 처리량은 H/W 환경에 종속되지 않은 성능 지표이기 때문이다.

FLOPS

FLOPS(Floating-point operations per second)는 모든 연산을 고려하는 것이 아니라,
보다 중요한 연산만을 가지고 성능을 측정해야 한다는 관점의 성능 지표이고,
GFLOPS(Giga) 또는 TFLOPS(Tera)로 표현한다.

여기서 말하는 중요한 연산은 Floating-point operations(부동소수점 연산)이며,
이는 사칙 연산(+, -, *, ÷ ..)과 같은 산술 연산을 의미한다.

FLOPS는 특히 GPU의 성능을 나타낼 때 많이 사용 되는데,
FLOPS에서 타겟하는 부동소수점 연산이 AI 분야에서(행렬곱 등) 많이 사용되기 때문이다.

Benchmarks

앞서 실행 시간, MIPS, FLOPS와 같이 다양한 성능 지표에 대해서 언급했는데,
사용자가 이러한 지표를 사용하여 여러 컴퓨터(CPU)의 성능을 비교할 수 있을까?

사실 사용자가 직접 CPI, Clock 등을 이용해 특정 작업에 대한 실행 시간을 계산한다는 것은 어려운 일이다.
그래서 이러한 과정을 대신 해주고 사용자에게 성능 지표를 제공하는 Benchmarks 라는 것이 존재한다.

이러한 Benchmarks의 예시로는,
우리가 구매하려는 CPU/GPU 성능을 찾아보면 Geekbench 또는 Antutu를 볼 수 있는데 이것들이 Benchmarks의 대표적인 예시라고 말할 수 있다.

또한 연구 분야에서는 CPU의 성능 측정에 특화된 SPEC Benchmarks를 많이 활용하는데,
1988년에 만들어져 현재까지도 쓰이고는 있지만, 최근에는 SPEC 대신 AI와 관련된 GPU/NPU/TPU 등 Multi-Thread 관련 Benchmarks를 많이 활용하고 있는 추세이다.
(SPEC은 CPU 성능 측정을 위한 Single-Thread 위주의 Benchmakrs)

Amdahl's Law

암달의 법칙(Amdahl's Law)은 컴퓨터 시스템의 일부를 개선할 때 전체적으로 얼마만큼의 최대 성능 향상이 있는지 계산하는 데 사용된다. (Wikipedia)

암달의 법칙(아래 수식)을 통해서 성능이 얼마만큼 향상되었는지 알 수 있으며,
여기서 $P$는 개선에 의해 영향을 받는 실행시간, $S$는 성능 향상 비율을 의미한다.

예시

예를 들어, 부동 소수점 명령어 개선을 통해 2배 성능을 향상 시켰지만
전체 명령어 중 부동 소수점 명령어가 10% 수준이라고 했을 때 성능이 얼마만큼 향상되었는지 알아보자.

그렇다면 $P=0.1 \;,\; S=2$ 이고, 이를 암달의 법칙에 적용하면 아래와 같다.

개선을 통해서 전체 성능의 1.053배 정도 향상 시켰음을 알 수 있고,
이를 기존의 성능(실행 시간)에 곱해 개선 된 성능(실행 시간)을 알 수 있다.

여기서 우리가 한가지 알 수 있는 점이 있는데,
시스템을 개선할 때 가장 중요한 Component 부터, 즉 가장 큰 비중을 차지하는 Component부터
개선해야 유의미한 성능 향상을 도출할 수 있고, 이는 실제 연구를 진행할 때도 중요한 요소이다.